가중치 초기화(Weight Initialization)
신경망을 학습할 때 손실 함수에서 출발 위치를 결정하는 방법이 모델 `초기화(initialization)`이다. 특히 가중치는 모델의 파라미터에서 가장 큰 비중을 차지하기 때문에 가중치의 초기화 방법에 따라 학습 성능이 크게 달라질 수 있다.
상수 초기화
신경망의 가중치를 모두 0으로 초기화하여 뉴런의 가중치가 0이면 가중 합산 결과는 항상 0이 되고, 활성 함수는 가중 합산 결과인 0을 입력받아서 늘 같은 값을 출력한다. 예를 들어 활성 함수가 ReLU나 하이퍼볼릭 탄젠트면 출력은 0이 되고 시그모이드면 출력은 항상 0.5가 된다. 0이 아닌 다른 값의 경우에도 만약 가중치를 모두 같은 상수로 초기화하면 신경망에 `대칭성(symmetry)`이 생겨서 같은 계층의 뉴런이 똑같이 작동하기 때문에 여러 뉴런을 사용하는 효과가 사라지고 하나의 뉴런만 있는 것과 같아진다. 즉, 모델을 크게 설계했더라도 모든 계층에 뉴런이 하나인 아주 작은 모델과 같아져 성능에 심각한 제약이 생긴다. 따라서 대칭성을 피하려면 가중치를 모두 다른 값으로 초기화해야 한다.
가우시안 분포 초기화
가중치를 균등 분포나 가우시안 분포를 따르는 `난수(random number)`를 이용해서 초기화하는 경우가 있다. 여기서 만약, 모델으리 가중치를 아주 작은 난수로 초기화한다면 입력 데이터가 여러 계층을 지날수록 점점 0에 가깝게 변하다가 값이 0이 되는 순간 뉴런의 가중 합산이 0이 되어 가중치를 0으로 초기화했을 때와 비슷한 현상이 일어난다. 반대로 가중치를 매우 큰 난수로 초기화한다면 입력 데이터가 각 계층을 지나면서 점점 1이나 -1로 변하는 현상이 발생한다. 이는 가중치가 크면 뉴런의 출력이 커지므로 데이터가 계층을 여러 번 통과할수록 출력은 점점 커진다. 여기에 만약 활성 함수가 하이퍼볼릭 탄젠트일 경우 출력이 더 커지지 못하고 -1과 1 사이에 포화하게 되고 이 경우 그레이디언트도 0으로 포화하여 그레이디언트 소실이 생겨 학습이 중단된다. 따라서, 적정한 가중치는 데이터가 계층을 통과하더라도 데이터의 크기를 유지해 주는 가중치로 초기화해야 한다.
Xavier 초기화
`Xavier 초기화(Xavier initialization)`는 시그모이드 계열의 활성 함수를 사용할 때 가중치를 초기화하는 방법이다. 이는 입력 데이터의 분산이 출력 데이터에서 유지되도록 가중치를 초기화한다. Xavier 초기화 방식을 유도하기 위해 다음과 같은 가정이 필요하다.
- 활성 함수를 선형 함수로 가정한다.
- 입력 데이터가 0 근처의 작은 값이라 가정하면 이는 시그모이드 계열의 활성 함수의 가운데 부분을 지나간다.
- 시그모이드 계열의 활성 함수의 가운데 부분은 직선에 가까워 선형 함수로 가정할 수 있다.
- 입력 데이터와 가중치는 다음과 같은 분포의 성질을 가진다.
- 입력 데이터와 가중치는 서로 독립이며, i.i.d를 만족한다.
- 입력 데이터와 가중치는 평균이 0인 분포를 따른다.
이러한 가정 속에서 Xavier 초기화 식을 유도해보면 다음과 같다.

Xavier 초기화는 가중치의 분산이 입력 데이터의 개수 n에 반비례하도록 초기화하는 방식이다. 가중치 분포는 가우시안 분포 또는 균등 분포로 정의할 수 있다. 신경망의 활성 함수가 시그모이드 계열일 때 Xavier 초기화를 적용하면 입력 데이터가 분산을 유지하면서 흘러가게 되므로 출력값이 0으로 변하거나 -1, 1로 포화되는 현상도 없어진다. 결과적으로 그레이디언트 소실이 사라져서 신경망의 학습이 원활히 진행된다.
He 초기화
ReLU는 양수 구간에서는 Xavier 초기화의 선형 가정이 유효하지만, 음수 구간에서는 입력 데이터가 0이 되면서 전체 입력 데이터의 50%가 0이 되어 입력 데이터의 크기, 즉 분산이 절반으로 줄어들어 가정이 맞지 않는다. 따라서 활성 함수가 ReLU일 때 Xavier 초기화를 적용하면 입력 데이터가 계층을 통과하면서 분산이 점점 줄어들어 출력이 0이 된다. 이렇듯 활성 함수가 ReLU일 때 Xavier 초기화의 한계점을 개선한 방식을 `He 초기화(He Iitialization)`이라고 한다.
He 초기화도 Xavier 초기화와 같이 뉴런의 입력 데이터와 출력 데이터의 분산을 같게 만들어준다. He 초기화는 ReLU를 사용했을 때 출력의 분산이 절반으로 줄어들기 때문에 가중치의 분산을 두 배로 키운다. 즉, Xavier 초기화가 가중치의 분산을 1/n으로 하면, He 초기화는 가중치의 분산을 2/n으로 한다.
정규화(Regularization)
신경망을 학습할 때는 최적화에 좋은 위치에서 출발하도록 초기화를 잘하는 것과 더불어, 최적해로 가는 길을 잘 찾을 수 있는 `정규화(regularization)`하는 것이 중요하다. 정규화는 최적화 과정에서 최적해를 잘 찾도록 정보를 추가하는 기법으로, 최적화 과정에서 성능을 개선할 수 있는 포괄적인 기법들을 포함한다. 이 기법들에는 최적해가 어떤 공간에 있는지 알려주어 빠르게 찾을 수 있도록 하거나, 손실 함수를 부드럽게 만들어 최적해로 가는 길을 잘 닦아주기도 하고, 최적해 주변을 평평하게 만들어서 새로운 데이터에 대해서도 모델이 좋은 성능을 갖도록 만들어 주기도 한다. 또한 모델과 데이터에 확률적 성질을 부여하여 비슷하지만 조금씩 다른 다양한 상황에서 학습하는 효과를 줄 수 있다.
일반화 오류
`일반화(generalization)`란 훈련 데이터가 아닌 새로운 데이터에 대해 모델이 얼마나 잘하는지를 가리키는 것으로, 모델의 성능이 좋다는 것은 일반화가 잘 되었다는 의미이다. 모델의 훈련 성능과 검증/테스트 성능의 차를 `일반화 오류(generalization error)`라고 하며 일반화 오류가 적을수록 일반화가 잘 된 모델이다. 정규화는 일반화를 잘하는 모델을 만드는 기법이라고도 한다. 신경망은 모델이 크고 복잡하기 때문에 파라미터 공간이 크고 학습 데이터가 많이 필요하다. 따라서 과적합되기 쉽기 때문에 신경망을 학습할 때는 반드시 여러 정규화를 적용하여 성능을 향상시켜야 한다.
정규화 접근 방식
정규화의 정의가 포괄적이기 때문에 기법도 다양하지만, 기본적인 접근 방법은 다음과 같이 몇 가지로 정리할 수 있다.
- 모델을 최대한 단순하게 만든다 → L1 정규화, 베이지안 정규화
- 단순한 모델은 복잡한 모델보다 파라미터 수가 적어서 과적합이 덜 생긴다
- 사전 지식을 표현해서 최적해를 빠르게 찾도록 한다 → 가중치 감소
- 확률적 성질을 추가한다 → 데이터 증강, 잡음 주입, 드롭아웃
- 데이터 또는 모델, 훈련 기법 등에 확률 성질을 부여하여 조금씩 변화된 형태로 데이터를 처리함으로써 다양한 상황에서 학습하는 효과
- 손실 함수는 풍부한 데이터를 이용해서 넓은 범위에서 세밀하게 표현되어 정확한 해를 찾을 수 있고, 모델의 잡음에 대해 민감하게 반응하지 않음
- `강건성(robustness)` : 어떤 변화가 있더라도 모델이 성능을 유지하는 성질
- 여러 가설을 고려하여 예측한다 → 앙상블 기법
- 하나의 모델로 예측하지 않고 여러 모델로 동시에 예측해서 그 결과에 따라 최종 예측하는 방식
- 하나의 모델이 가질 수 있는 편향을 제거하여 오차를 최소화하고 공정하게 예측
배치 정규화(Batch Normalization)
신경망 학습이 어려운 이유 중 하나는 계층을 지날 때마다 데이터 분포가 보이지 않는 요인에 의해 조금씩 왜곡되기 때문이다. 데이터 왜곡을 막기 위해선 가중치 초기화를 잘해야 하고 학습률도 작게 사용해야 하는데, 이 경우 학습 속도가 느려지는 문제가 발생한다.
내부 공변량 변화
분포를 결정하는 보이지 않는 요인을 내부 공변량이라고 한다. 데이터 분포가 보이지 않는 요인에 의해 왜곡되는 현상을 `내부 공변량 변화(internal covariate shift)`라고 한다. 내부 공변량이 바뀌면 각 계층의 데이터 분포가 원래 분포에서 조금씩 멀어져 하위 계층의 작은 변화가 상위 계층으로 갈수록 큰 영향을 미치게 된다. 그 결과 작은 계층의 작은 변화가 상위 계층으로 갈수록 큰 영향을 미친다.
배치 정규화 단계
`배치 정규화(batch normalization)`는 데이터가 계층을 지날 때마다 매번 정규화해서 내부 공변량 변화를 없애는 방법이다. 배치 정규화를 하면 모델이 실행될 때마다 해당 계층에서 매번 정규화가 일어난다. 또한 전체 데이터에 대해 정규화하지 않고 미니배치에 대해 정규화를 진행한다.
표준 가우시안 분포로 정규화
d 차원의 입력 데이터가 있다면 배치 정규화는 차원별로 평균과 분산을 구해서 표준 가우시안 분포 N(0,1)로 정규화한다. 배치 정규화를 모든 계층에 적용하면 데이터가 계층을 지날 때마다 표준 가우시안 분포로 정규화되고 이를 통해 데이터의 크기가 작아지면서 내부 공변량의 변화를 최소화할 수 있다. 원리적으로는 계층을 지나면서 생기는 데이터 오차의 크기를 줄임으로써 누적 오차도 작게 만드는 작업을 한 것이다.
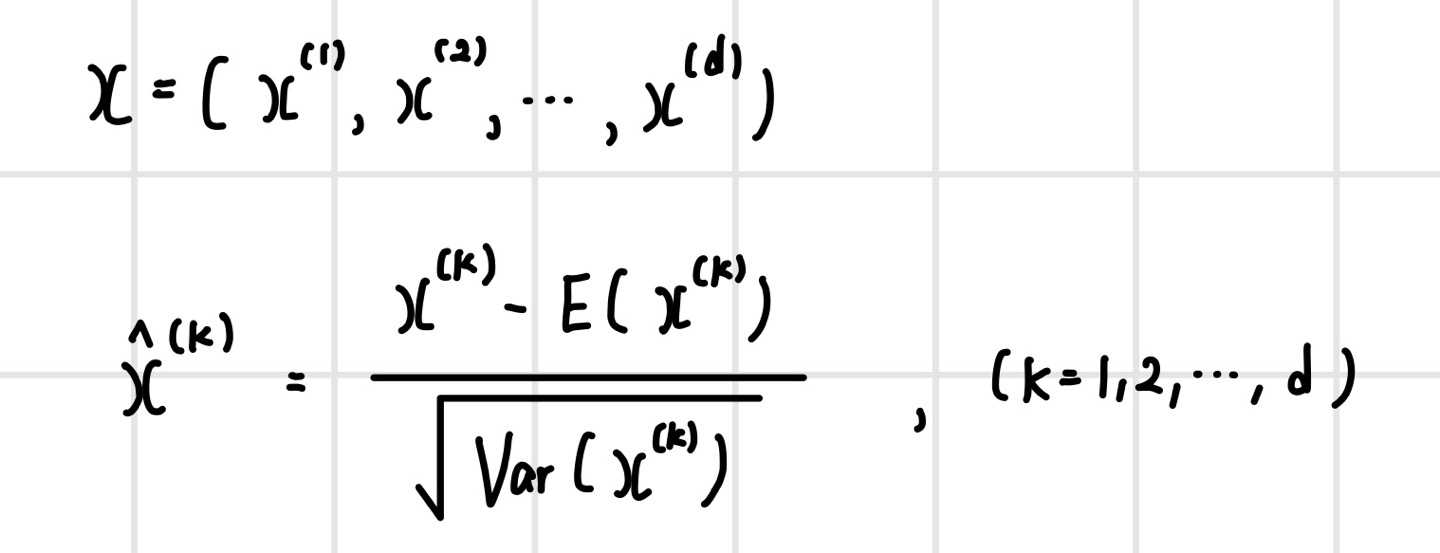
원래 분포로 복구
데이터를 표준 가우시안 분포로 정규화하면 모델이 표현하려던 비선형성을 제대로 표현할 수 없는 문제가 발생한다. 예를 들어 시그모이드 함수의 경우 정규화된 모든 데이터는 함수의 가운데 부분인 선형 영역을 통과하므로 비선형성이 사라진다. ReLU의 경우에도 정규화된 데이터의 절반은 음수이기 때문에 50% 데이터의 출력이 0이 되어 뉴런의 절반이 죽은 ReLU가 되면 학습이 제대로 이루어지지 않는다.

따라서 배치 정규화를 하면서 모델의 비선형성을 잘 표현하려면 데이터를 표준 가우시안 분포로 정규화한 뒤 다시 원래 데이터의 분포로 복구해야한다. 이는 원래 데이터 분포의 평균과 표준편차를 통해 정규화된 데이터를 다음과 같이 복구할 수 있다.
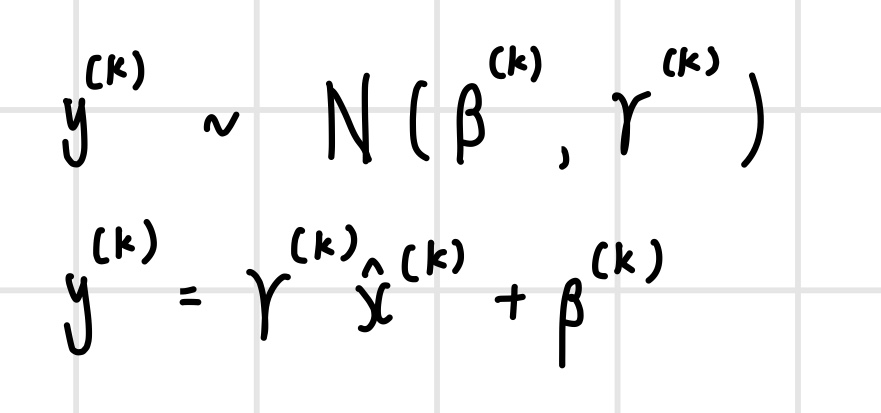
그러나 여기서 문제는 미니배치에 대한 평균과 표준편차가 원래 데이터의 분포를 표현한다면 바로 복구가 가능하지만, 실제 미니배치에 대한 평균과 표준편차가 원래 데이터 분포를 표현하지 못한다는 것이다. 따라서 원래 데이터 분포의 평균과 표준편차는 모델의 학습 과정에서 따로 구해야 한다.
배치 정규화 알고리즘
배치 정규화의 학습 알고리즘은 다음과 같다. 미니배치의 평균과 분산을 구해서 표준 가우시안 분포로 정규화를 수행한다. 이후 다시 학습된 평균과 표준편차를 이용해서 원래 분포로 복구한다.

학습 단계에서는 미니배치 단위의 평균과 분산으로 정규화를 수행하지만, 테스트 단계에서는 전체 데이터의 평균과 분산으로 정규화해야 한다. 전체 데이터의 평균과 분산은 표본의 평균과 분산을 이용해서 모분포의 평균과 분산을 구하는 식을 통해 다음과 같이 계산이 가능하다. 구현할 때는 학습 단계에서 미니배치 단위로 구한 평균과 분산에 대해 `이동 평균(moving average)`를 구해서 전체 데이터의 평균과 분산을 계산한다.
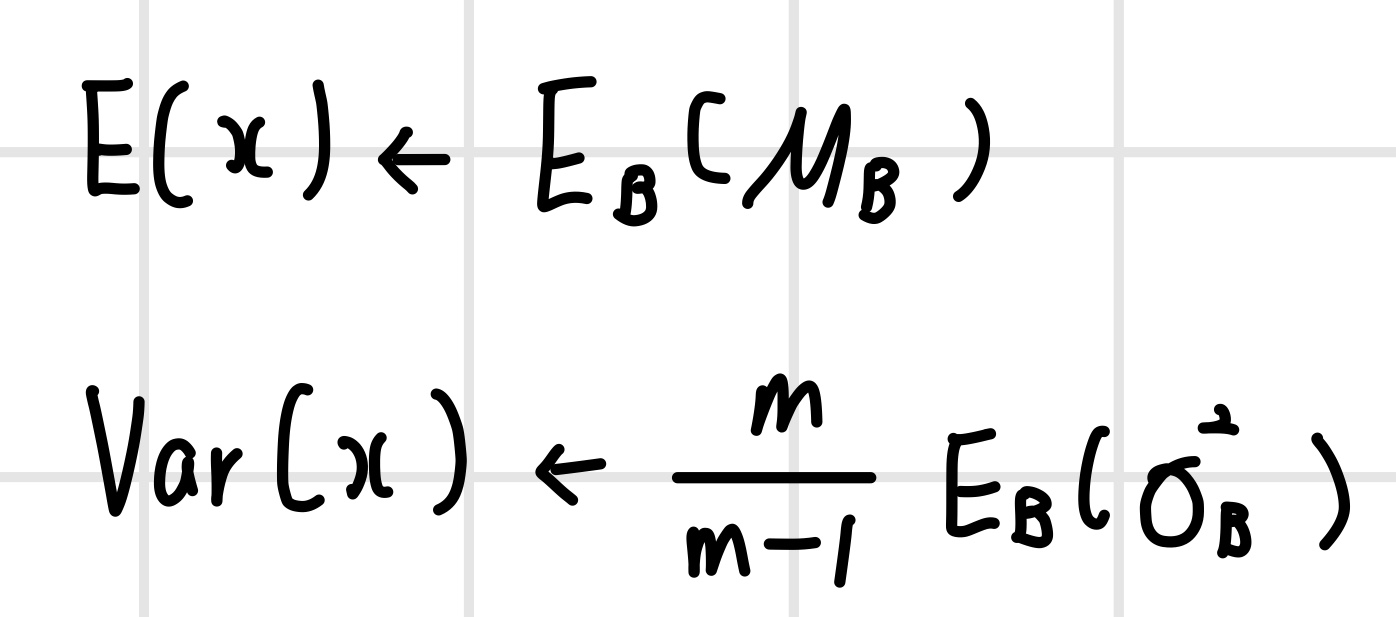
배치 정규화를 처음 제안했을 때는 뉴런의 가중 합산과 활성 함수 사이에서 수행하는 것으로 제안했다. 그러나 향후 연구를 통해 활성 함수를 실행한 뒤에 배치 정규화를 수행했을 때 더 나은 성능을 보이기도 했다. 일반적으로 가중 합산한 뒤에 배치 정규화를 적용하지만, 모델의 성능을 세밀하게 개선하려면 활성 함수 이후에 적용했을 때 성능도 검증해 볼 필요가 있다.
이미지 정규화 기법
배치 정규화를 이미지에 적용할 때는 채널 단위로 정규화를 수행하며, 배치 정규화 이외에 좀 더 세분된 정규화 방식을 사용한다. 이미지의 경우 차원이 높기 때문에 뉴런 단위보다는 뉴런의 묶음인 채널 단위로 배치 정규화를 수행한다. RNN의 경우 이미지 샘플별로 정규화하는 방식인 `계층 정규화(layer normalization)`을 사용하며, 이는 미니배치 크기와 무관하다. 스타일 변환이나 GAN에서는 샘플의 채널별로 정규화하는 `인스턴스 정규화(instance normalization)`를 사용하고, 미니배치 크기가 작을 때는 샘플의 채널 그룹을 나눠서 정규화하는 `그룹 정규화(group normalization)`을 사용하기도 한다.
배치 정규화의 우수성
- 내부 공변량 변화가 최소화되므로 그레이디언트의 흐름이 원활해지고 학습이 안정적으로 진행
- 지속적으로 데이터 분포를 유지하기 때문에 초기화 방법에 대한 의존도가 낮아지고 높은 학습률을 사용 가능
- 미니배치 단위로 정규화하므로 어떤 샘플의 조합으로 미니배치를 구성하는지에 따라 데이터가 조금씩 변형되어 확률적 성질이 생기고 그에 따라 모델의 성능이 향상
- 내부 공변량 변화를 없애기보다는 손실과 그레이디언트 변화를 제약하여 곡면을 부드럽게 만들어 줌으로써 모델의 학습 성능이 향상된다는 것이 최근 연구 결과에 따라 증명
가중치 감소(weight decay)
최적화를 할 때는 다루는 숫자의 크기가 작을수록 오차의 변동성이 낮아지므로 파라미터 공간이 원점 근처에 있을 때 정확한 해를 빠르게 찾을 수 있다. 따라서 뉴런의 가중 합산 식을 표현할 때 가중치와 편향이 가장 작은 것이 좋다. `가중치 감소(weight decay)`는 학습 과정에서 작은 크기의 가중치를 찾게 만드는 정규화 기법이다.
가중치 감소 적용 방식
가중치 감소는 가중치의 크기를 제한하는 제약 조건으로 손실 함수의 일부 항으로 표현할 수 있다. 즉, 다음 식과 같이 손실 함수로 확장해서 가중치의 크기를 표현하는 `정규화 항(regularization term)`을 더하면 최적화 과정에서 손실 함수와 함께 정규화 항도 같이 최소화되므로 크기가 작은 가중치 해를 구할 수 있다. 여기서 람다(lambda)는 정규화 상수로서 가중치 크기를 조절하는 역할을 한다. 이 값이 커질수록 정규화 항의 비중이 커지면서 가중치 크기는 작아지고, 값이 작아지면 정규화 항의 비중이 작아지면서 가중치 크기는 커진다. 따라서 이 값에 따라 유효한 가중치의 개수가 달라질 수 있기 때문에 모델의 복잡도를 조정하는 역할을 한다고 볼 수 있다.
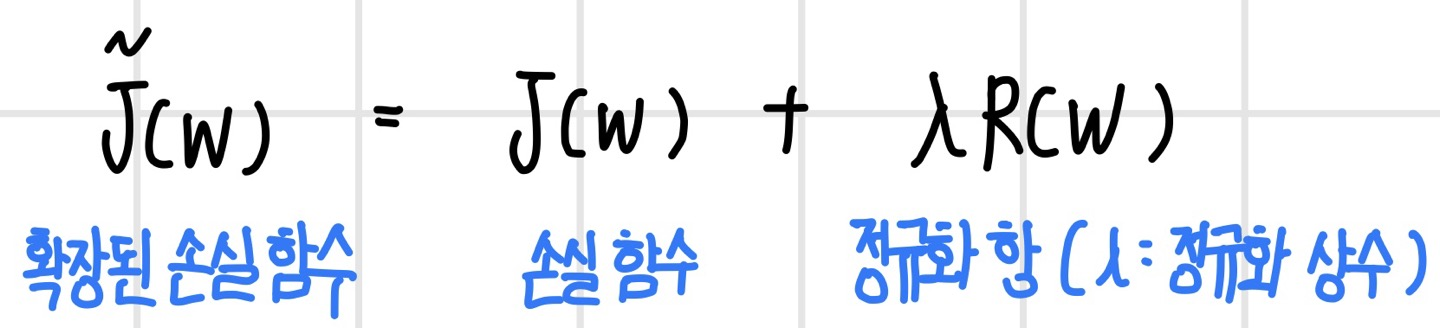
정규화 항 R(w)는 가중치의 크기를 나타내는 노름으로 정의한다. L2 노름을 사용하면 L2 정규화, L1 노름을 사용하면 L1 정규화라고 한다. 회귀 문제에서는 L2 정규화를 `리지 회귀(Ridge regression)`, L1 정규화를 `라소 회귀(Lasso regression)`이라고 부른다.

또한 가중치 그룹별로 가중치 크기를 조절하고 싶다면 가중치 그룹별로 정규화 항을 분리해서 합산 형태로 표현한다. 이를 통해 신경망의 계층별로 가중치 크기가 다른 경우 통제가 가능하다.

가중치의 사전 분포와 노름
정규화 항에 어떤 노름을 사용할지는 가중치의 사전 분포에 따라 달라진다. 만약 가중치의 사전 분포가 가우시안 분포라면 L2 노름을 사용하고, `라플라스 분포(Laplace distribution)`라면 L1 노름을 사용한다. 가중치의 사전 분포를 모르는 경우 일반적으로 L2 노름을 사용한다. 정규화 항은 손실 함수의 일부이므로 최대 우도 추정 방식에 따라 가중치의 사전 분포에 음의 로그 우도를 구해서 표현할 수 있다. 먼저 `다변량 가우시안 분포(Multivariate Gaussian distribution)`의 정의는 다음과 같다.

해당 식에서 가중치의 사전 분포가 가우시안 분포일 경우 음의 로그 우도를 취했을 때 가중치의 L2 노름의 제곱이 도출된다.

가중치의 사전 분포가 라플라스 분포인 경우에도 음의 로그 우도를 취하면 L1 노름이 유도된다.

정규화 효과
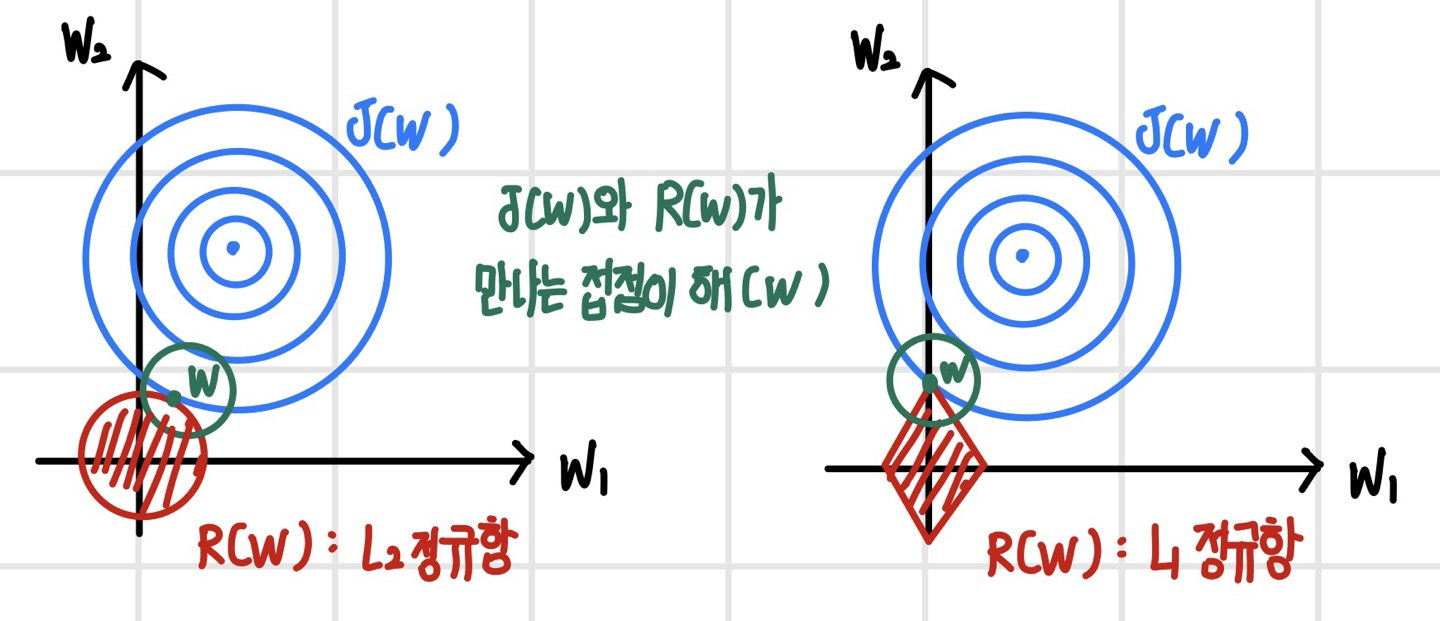
L2 정규화와 L1 정규화의 효과는 약간 다르다. 다음 그림은 가중치 감소 정규화를 적용했을 때 해의 위치를 나타냈다. 손실 함수와 각 정규항이 만나는 접점이 가중치 감소를 적용한 확장된 손실 함수의 해가 된다. L2 정규화의 경우 손실 함수 J(W)가 어느 방향에 있던 L2 정규항과 닿을 확률은 같기 때문에 최적해는 원점 주변에 존재한다. 그러나 L1 정규화의 경우 손실 함수가 L2 정규항의 모서리에 먼저 닿을 확률이 사선에 닿을 확률보다 높기 때문에 최적해가 특정 차원의 축 위에 있을 가능성이 높다. 이 경우 최적해가 존재하는 축을 제외한 나머지 축의 좌푯값은 0이 되므로, 좌표의 대부분이 0이 되어 희소한 해를 가지게 된다. 가중치가 희소해지면 일부 가중치가 0이 되어 유효 파라미터 수가 줄어들고 작은 모델이 되어 성능이 빨라진다. 이러한 과정은 `유효한 특징을 선택(Feature Selection)`하는 과정으로도 볼 수 있다.
조기 종료(early stopping)
`조기 종료(early stopping)`는 과적합이 일어나기 전에 훈련을 멈춤으로써 과적합을 피하는 정규화 기법이다. 과적합이 일어나면 훈련 성능은 계속 좋아지지만 테스트/검증 성능은 좋아지다가 다시 나빠진다. 훈련하는 동안 주기적으로 성능 검증을 하다가 성능이 더 좋아지지 않으면 과적합이 시작되었다고 판단하고 훈련을 멈춘다. 보통 `에폭(epoch)` 단위로 성능 검증을 하며 더 자주 검증을 해야할 때는 배치 실행 단위로 검증하기도 한다. 에폭은 전체 훈련 데이터를 한 번 사용해서 훈련하는 주기를 말한다. 보통 훈련 시에는 여러 에폭에 걸쳐서 훈련한다.
조기 종료 기준
조기 조욜에서 유의할 점은 모델의 성능이 향상하지 않았더라도 바로 훈련을 종료해서는 안된다는 점이다. 신경망을 학습할 때 단계마다 미니배치로 근사한 그레이디언트는 실제 그레이디언트와 차이가 있기 때문에 성능은 조금씩 좋아졌다가 나빠질 수 있다. 따라서 일시적인 성능 변동이 아니라 지속적인 성능의 정체 또는 하락이 판단되면 그때 훈련을 종료하는 것이 바람직하다. 보통 일정 횟수 동안 성능이 연속적으로 좋아지지 않는지 모니터링해서 훈련을 종료한다. 또한 성능의 기준은 모델 오차 혹은 정확도 등 다양한 성능 측도를 사용할 수 있다. 테스트 시점에는 훈련이 끝난 마지막 상태의 모델 혹은 훈련 성능이 가장 좋은 모델 상태를 저장한 후 사용한다.
조기 종료의 정규화 효과
조기 종료는 파라미터 공간을 작게 만드는 효과가 있다. 다음 그림과 같이 파라미터 공간은 초기 파라미터 위치를 중심으로 제약된다. 조기 종료로 파라미터 공간의 크기가 제약되면 L2 정규화와 동일한 효과가 있다. 만약 손실 함수가 2차 함수로 정의되는 선형 모델의 경우 조기 종료와 L2 정규화는 동일하다.

데이터 증강(data augmentation)
모델은 복잡한데 그만큼 충분한 훈련 데이터가 제공되지 않으면 모델이 데이터를 암기해서 과적합이 발생한다. 과적합을 막는 가장 근본적인 방법은 훈련 데이터이 양을 늘리는 것이다. 그러나 현실적으로 데이터 레이블을 만드는 비용이 만만치 않으며, 일부 데이터는 수집이 매우 까다롭다. 따라서 데이터를 수집해서 큰 데이터셋을 만드는 방법보다, 훈련 데이터셋을 이용해서 새로운 데이터셋을 생성하는 `데이터 증강(data augmentation)` 기법과 같이 쉽게 데이터를 늘려주는 방법이 필요하다.
데이터 증강 기법
가장 기본적인 증강 방법은 훈련 데이터를 조금씩 `변형(transformation)`해서 새로운 데이터를 만드는 방법이다. 데이터 증강 규칙을 사람이 정할 경우 증강된 데이터가 성능에 최적인지는 검증이 필요하다. 다른 방법으로는 훈련 데이터의 분포를 학습해서 `생성 모델(generative model)`을 만든 뒤에 새로운 데이터를 생성하는 방법이 있다. 생성 모델을 이용하면 더 쉽게 현실감 있는 데이터로 합성하거나 변형할 수 있다. 데이터를 증강해서 미리 훈련 데이터셋에 추가해 둘 수도 있겠지만, 데이터를 확률적으로 변형하면 무수히 많은 변형이 생겨 일반적으로는 훈련 과정에서 실시간으로 데이터를 증강한다. 즉, 훈련 데이터를 읽어서 모델에 입력하기 전에 데이터를 증강한다.
데이터 증강을 할 때는 `클래스 불변 가정(class-invariance assuption)`을 따라야 한다. 클래스 불변 가정이란 데이터를 증강할 때 클래스가 바뀌지 않도록 해야 한다는 가정이다. 만일 데이터 증강 과정에서 클래스의 결정 경계를 넘어서면 다른 클래스로 인식하므로, 각자의 결정 경계 안에서 데이터를 변형해야 한다.
배깅(bagging)
`앙상블(ensemble)`은 여러 모델을 실행해서 하나의 강한 모델을 만드는 방법이다. 개별 모델의 성능은 약하지만, 약한 모델이 모여서 하나의 팀을 이루면 성능이 좋은 강한 모델이 될 수 있다. 앙상블 기법 중 `배깅(bagging: bootstrap aggregating)`은 독립된 여러 모델을 동시에 실행한 뒤 개별 모델의 예측을 이용해서 최종으로 예측하는 방법이다. 배깅이 정규화 방법인 이유는 모델이 서로 독립일 때 예측 오차가 모델의 수에 비례해서 줄어들기 때문이다.
배깅의 원리
배깅은 모델의 종류와 관계없이 다양한 모델로 팀을 구성할 수 있다. 같은 종류의 모델로 팀을 구성하기도 하며, 다른 종류의 모델로 구성하기도 한다. 하지만 성능을 높이기 위해선 모델 간에 독립을 보장해야 한다. 모델의 독립성을 보장하기 위해 훈련 데이터를 `부트스트랩(bootstrapping)`하여 모델별로 부트스트랩 데이터를 생성한다. 부트스트랩 하는 과정에서 훈련 데이터에서 복원 추출을 하기 때문에 동일한 데이터가 다시 추출될 수 있으며, 일반적으로 부트스트랩 데이터의 크기는 훈련 데이터와 동일하게 한다.
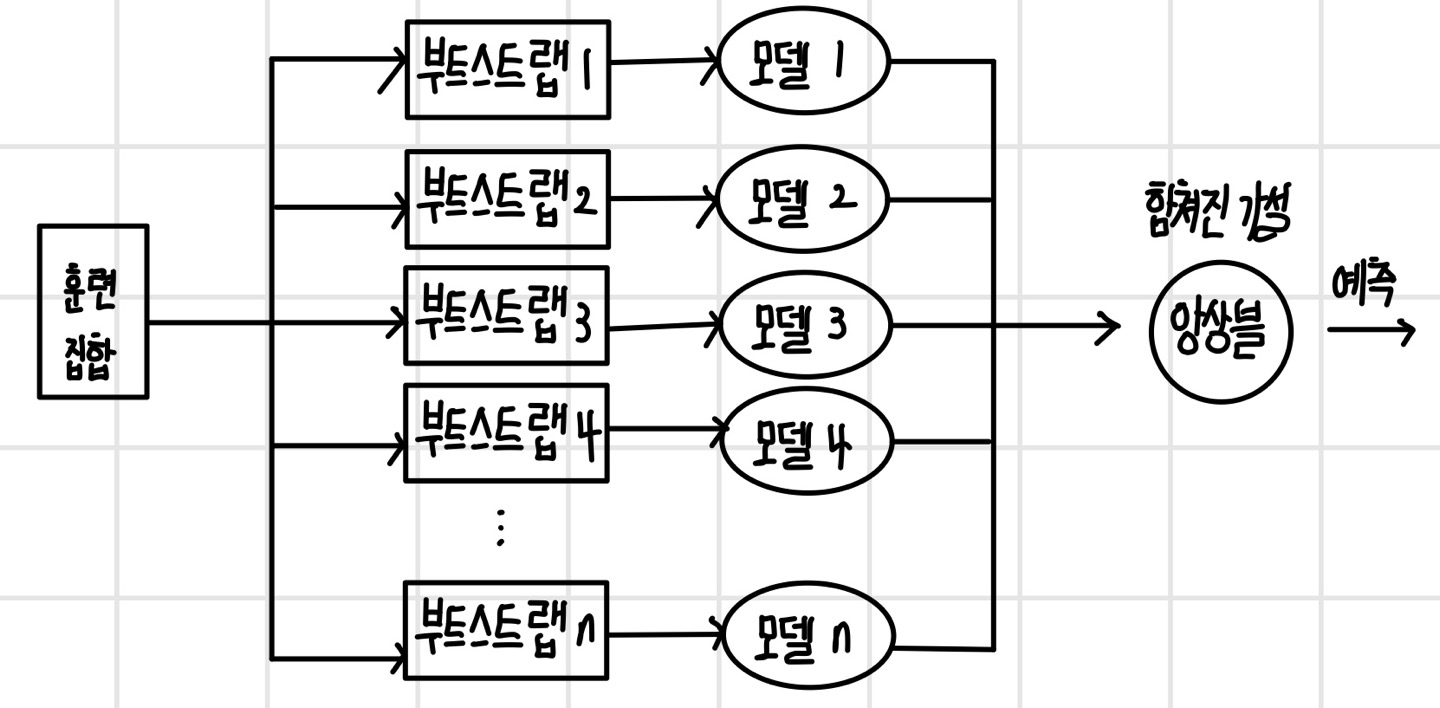
추론 단계에서는 개별 모델이 결과를 집계해서 예측한다. 일반적으로 회귀 모델의 경우 개별 모델의 결과를 평균해서 예측하며, 때에 따라 모델의 비중을 다르게 두고 가중 합산을 하기도 한다. 분류 모델의 경우 가장 많이 나온 값으로 예측하는 `다수결 투표 방식(majority voting)`을 사용한다. 때에 따라 개별 모델을 임의로 선택해서 예측하거나 투표 방식을 변형해서 사용하기도 한다.
신경망 모델로 배깅할 때는 부트스트랩을 사용하지 않아도 된다. 모델의 가중치를 랜덤하게 초기화하는 만큼 마치 다른 모델인 것과 같은 효과가 생기고, 미니배치 방식을 사용함으로써 모델별로 다른 훈련 데이터셋을 사용하는 효과가 있기 때문이다. 또한 인공 신경망 모델은 다른 모델에 비해 크기가 크기 때문에 보통 앙상블 크기를 20이 넘지 않게 사용한다. 참고로 앙상블 기법에는 배깅 외에 부스팅이 있다. 그러나 부스팅은 큰 모델을 방식이며 정규화 방법은 아니며 배깅은 모델의 오차를 줄여주는 정규화 방식이다.
배깅의 정규화 효과
배깅의 정규화 효과를 확인하기 위해 k개의 회귀 모델로 배깅한다고 가정한 경우 개별 모델의 예측 오차가 배깅에서 어떻게 줄어드는지 확인해보면 다음과 같다. 이 경우 개별 회귀 모델의 예측 오차는 평균이 0이고 분산이 v이며 모델 간의 공분산이 c인 가우시안 분포를 따른다.

회귀 모델에서 배깅의 예측은 개별 모델의 예측값의 평균으로 계산하므로 배깅의 오차는 개별 모델 오차의 평균이 된다.
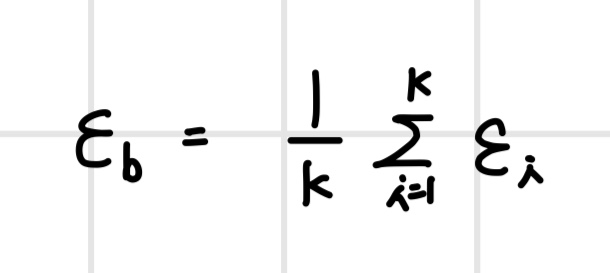
배깅을 해서 오차가 줄어들었는지 확인하기 위해 배깅의 오차의 분산을 계산한다. 이때 배깅의 오차의 평균은 0이다.

이제 개별 모델이 독립인 경우와 독립이 아닌 경우에 배깅의 예측 오차의 분산이 어떻게 확인해본다. 만약 개별 모델들의 상관성이 매우 커 공분산과 분산이 같다고 가정하면(즉, C = V) 다음과 같은 분산을 가진다. 따라서 모델 간에 상관성이 높으면 배깅했을 때 오차가 줄어들지 않는다.
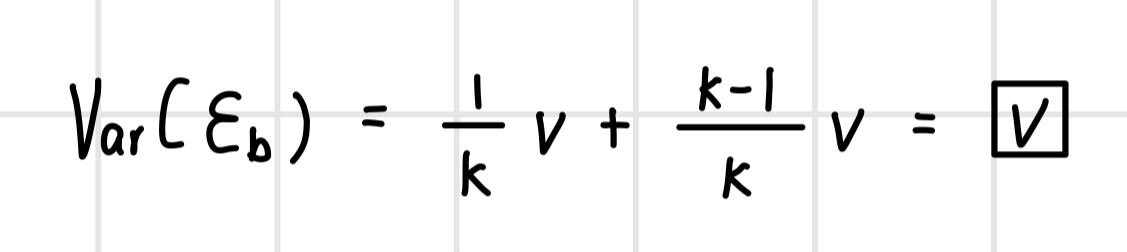
하지만 개별 모델들이 서로 독립이라면 공분산은 0이 되기 때문에 C가 0이 되어 배깅의 예측 오차는 다음과 같이 모델 수에 비례하여 줄어든다. 따라서 배깅을 하는 경우 개별 모델의 독립을 보장한다면 모델 수에 비례해서 오차를 줄일 수 있다.

드롭아웃(Dropout)
`드롭아웃(Dropout)`은 미니배치를 실행할 때마다 뉴런을 랜덤하게 잘라내서 새로운 모델을 생성하는 정규화 방법이다. 드롭아웃은 하나의 신경망 모델에서 무한히 많은 모델을 생성하는 배깅과 같다. 이는 계산 시간이 거의 들지 않고 다양한 모델에 쉽게 적용할 수 있는 강력한 정규화 기법이다. 그러나 서로 독립된 모델을 병렬로 실행해서 예측 오차를 줄이는 배깅과는 다르게 드롭아웃은 모델 간에 파라미터를 공유하기 때문에 상관성이 발생하여 더 좋은 성능을 갖기는 어렵다. 하지만 드롭아웃은 모델을 병렬로 실행하지 않고도 무한히 많은 모델의 평균으로 예측하는 효과가 있기 때문에 배깅보다 실용적인 정규화 방법이다.

학습 단계
드롭아웃은 미니배치를 실행할 때마다 뉴런을 랜덤하게 잘라내서 새로운 모델을 생성한다. 뉴런을 드롭아웃할 때는 뉴런의 50% 이상은 유지되어야 하며, 입력 계층과 은닉 계층에 적용한다. 뉴런을 유지할 확률은 입력 뉴런은 0.8, 은닉 뉴런은 0.5 정도로 지정한다. 훈련 단계에서 드롭아웃을 적용하기 위해서 계층별로 뉴런의 `이진 마스크(binary mask)`를 생성한다. 이는 뉴런별 드롭아웃 여부를 나타내며 뉴런의 마스크값이 1이면 뉴런은 유지되고 마스크값이 0이면 드롭아웃된다. 이진 마스크의 0과 1의 비율은 뉴런이 유지될 확률에 따라 정한다. 이후 계층의 출력에 이진 마스크를 곱하면 드롭아웃이 실행된다.

추론 단계
추론 단계에서는 뉴런을 드롭아웃하지 않고 훈련 과정에서 확률적으로 생성했던 다양한 모델의 평균을 예측해야 한다. 모델 평균을 어떻게 구하는지 확인하기 위해 입력 뉴런의 2개이고 출력 뉴런이 1개인 신경망에 뉴런을 유지할 확률 p를 0.5로 적용한다고 가정한다. 이 경우 총 4개의 모델이 확률적으로 생성되며, 네 모델의 평균을 계산하면 다음과 같은 결과를 얻는다.

결론적으로 모델 평균의 결과는 드롭아웃을 하지 않은 전체 모델의 출력과 뉴런 유지 확률 p의 곱으로 표현된다. 즉, 모델의 가중치를 p로 스케일링해서 모델 평균을 계산하는 `가중치 비례 추론 규칙(Weight scaling inference rule)`을 따른다. 따라서 추론 시에는 각 계층의 출력에 뉴런 유지 확률 p를 곱해주기만 한다.

그러나 뉴런을 유지할 확률 p를 반드시 추론 시점에 곱해야 하는 것은 아니다. 훈련 시점에 각 계층의 출력을 미리 p로 나눠 두면 원래의 추론 코드를 그대로 적용할 수 있다. 이런 아이디어를 적용한 방법이 `역 드롭아웃(Inverted dropout)`이다.
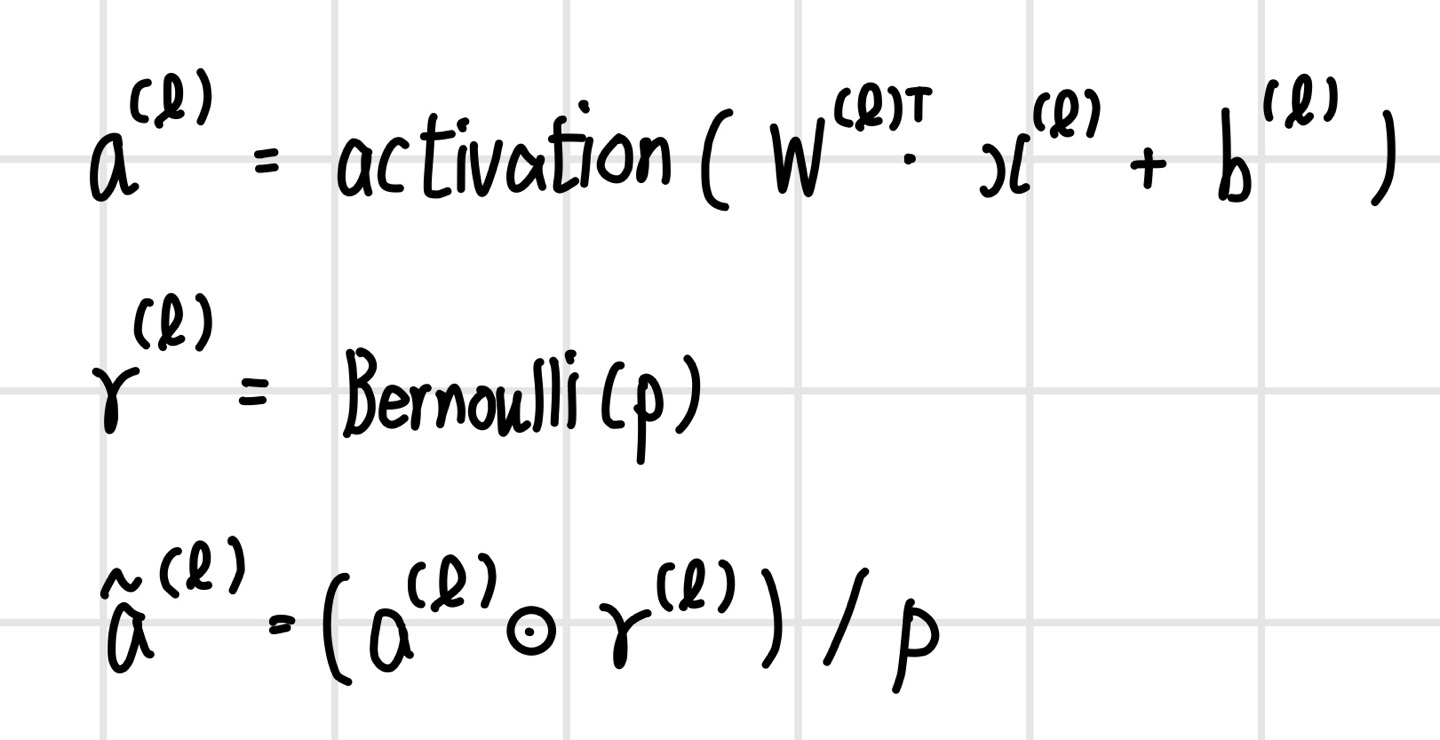
잡음 주입
데이터나 모델을 확률적으로 정의할 수 있다면 더 정확하게 추론할 수 있다. 그러나 데이터나 모델이 확률적으로 정의되지 않았다면 간단히 `잡음(noise)`을 넣어 확률적 성질을 부여할 수 있다. 즉, 현재 상태를 평균으로 보고 잡음으로 변형된 데이터를 생성해서 특정한 분포를 따르도록 만든다.
잡음 주입 방식
입력 데이터에 잡음 주입
- 데이터 증강 기법에 해당
- 입력 데이터에 아주 작은 분산을 갖는 잡음을 넣으면 가중치 감소와 동일한 정규화 효과
특징에 잡음 주입
- 데이터가 추상화된 상태에서 데이터 증강
- 추상화된 상태에서 확률적 성질을 부여하여 객체와 같은 상대적으로 의미 있는 단위로 데이터 증강이 일어나 성능이 크게 향상
모델 가중치에 잡음 주입
- 드롭아웃에서 뉴런을 제거할 때 확률적으로 가중치를 조절하기 때문에 가중치에 잡음을 넣는 것
- 가중치의 `불확실성(Uncertainty)`과 관련
- 베이지언 신경망은 가중치의 분포를 학습하며 가중치의 불확실성을 표현
- 가중치 분포의 분산이 크면 가중치의 불확실성이 높으며 분산이 작으면 불확실성이 낮음
- 가중치에 잡음을 직접 더해 가중치의 그레이디언트 크기를 작게 만드는 정규화 효과
- 최소 지점 주변이 평지로 변해 새로운 데이터에 대한 일반화 성능이 향상
소프트 레이블링
훈련 데이터의 레이블이 정확하지 않아 오차가 있다면 분류 모델이 정확히 1이나 0으로 예측하지 못하기 때문에 계속해서 일정량의 손실이 발생하고 최적화가 이루어지지 않을 수 있다. 이 경우 오차가 있다고 가정하고, 타깃 클래스의 확률은 오차만큼 작게 만들고 나머지 클래스들의 확률은 오차를 배분해서 확률을 부여한다. 이러한 방식을 `소프트 레이블링(soft labling)`이라고 한다. 레이블에 오차를 반영한 후 학습하면 모델 성능이 높아진다. 반대로 레이블을 0과 1로 만드는 것을 하드 레이블링이라고 한다.

이 포스팅은 'Do it! 딥러닝 교과서' 교재를 공부하며 쓴 글입니다.