순환 신경망 학습
학습이란 데이터를 통해 parameters를 추정한다는 것을 의미한다. 순환 신경망은 t시점까지의 과거 정보를 활용하여 y를 예측하게 되는데, 학습 대상이 되는 파라미터는 3가지이다. 첫 번째는 t 시점의 데이터를 반영한 W_xh 가중치, 두 번째는 t 시점 이전의 정보를 반영하는 W_hh 가중치, 그리고 t 시점의 y를 예측할 때 활용하는 W_hy 가중치이다. 해당 파라미터는 매 시점마다 공유하는 구조이며(parameter sharing), 매 시점 파라미터를 구성하는 값이 같다. 또한 최적의 W는 W를 매 시점 적용했을 때 Loss가 최소가 되는 W이다. hidden state와 예측값은 다음과 같이 계산된다.
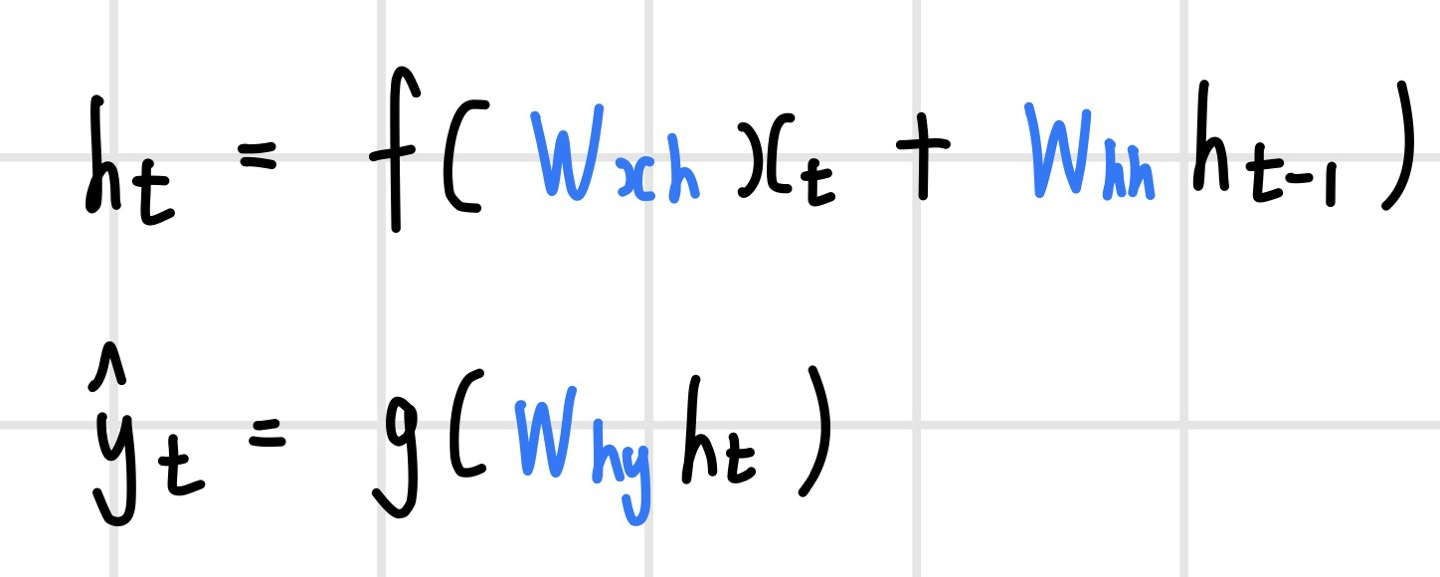
순환 신경망이 3가지의 가중치를 추론하는 학습과정은 다음과 같다.
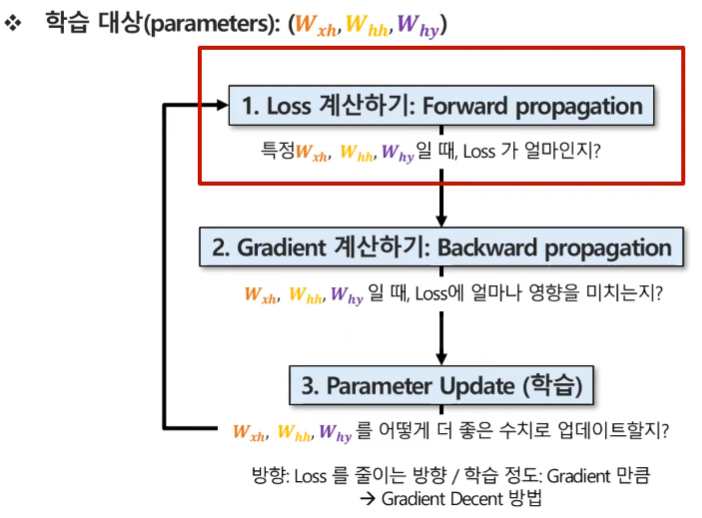
Loss 계산하기 : Forward propagation
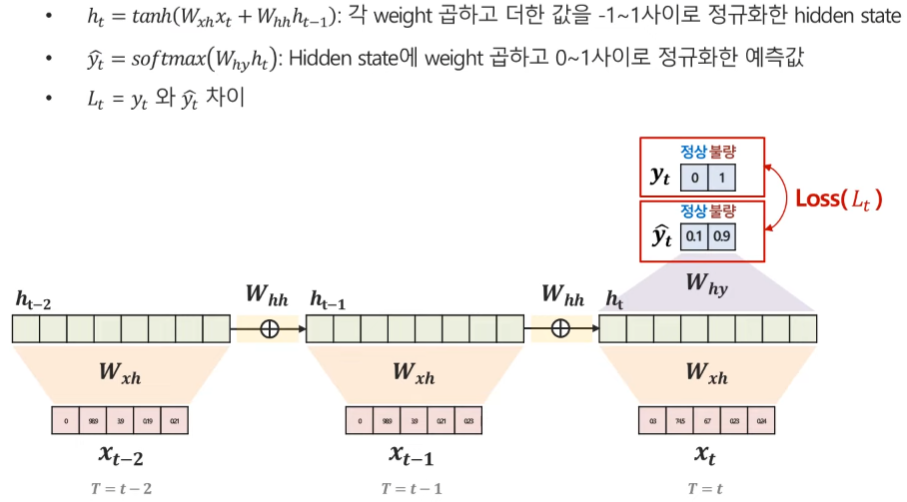
먼저 첫 번째로 Forward propagation, 즉 Loss 값을 계산하는 과정이다. hidden state h_t와 예측값, loss 값의 계산 방법은 다음과 같다. 여기서는 output이 1개인 경우를 고려했다.
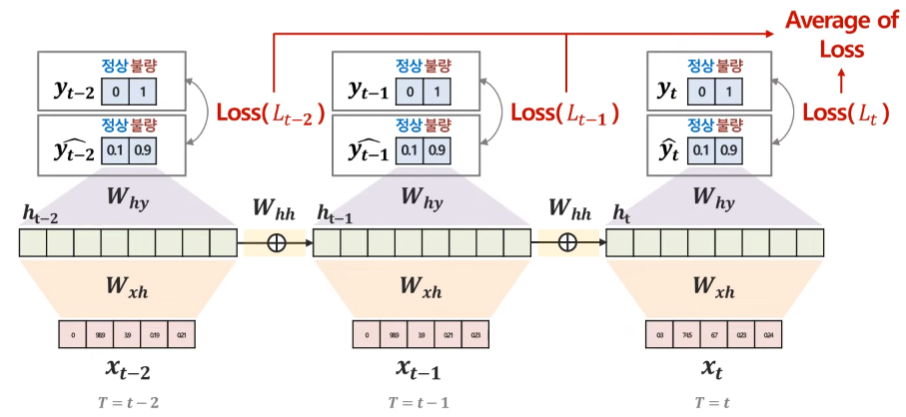
만약 one to many, many to many처럼 output이 많은 경우의 Loss 값은 각 시점별 loss의 평균을 전체 Loss로 활용한다.
Gradient 계산하기 : backward propagation
RNN에서는 backward propagation 과정을 Backward Propagation Through Time, BPTT를 통해 수행한다. 역전파 과정이란 결국 Loss 값을 최소로 해주는 Gradient를 계산하여 파라미터를 업데이트하는 과정에 더해주거나 빼주는 과정을 말한다. 먼저 W_hy의 Gradient를 계산하는 방법은 다음과 같다. Loss를 해당 가중치로 바로 미분하는 것이 어렵기 때문에 chain rule을 활용하여 미분을 수행한다.
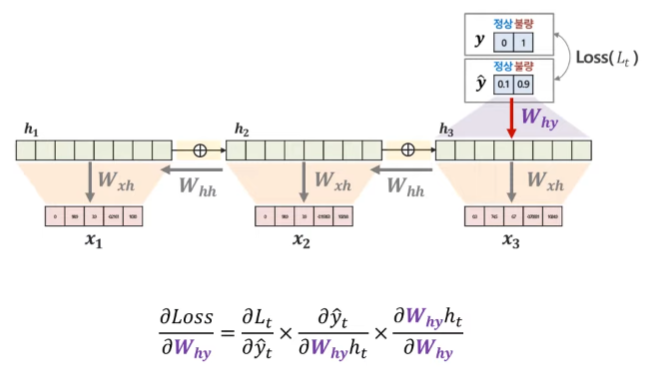
다음으론 W_hh 파라미터에 대한 Gradient를 계산하는 과정이다. W_hh의 경우 여러 시점에 있는 파라미터이기 때문에 모든 시점을 고려해야 한다. 만약 3번째 시점까지 데이터가 존재한다면 1번째, 2번째, 3번째 시점의 Gradient를 모두 계산해 더해주어야 한다.
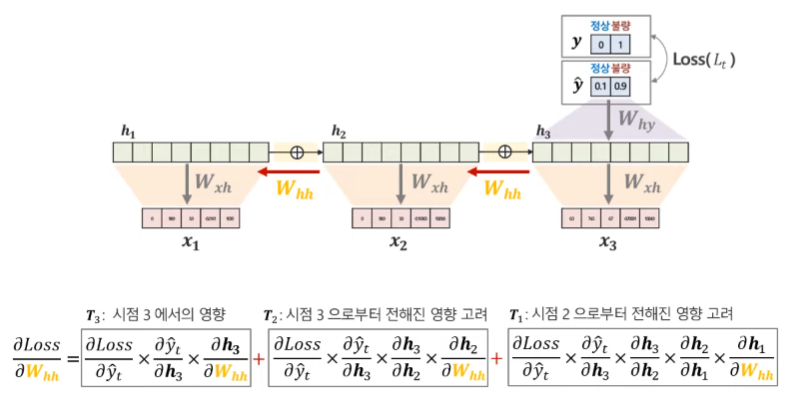
마지막으로 W_xh 또한 각 시점마다 나타나는 가중치이기 때문에, 모든 시점을 고려하여 Gradient를 계산해주어야 한다.
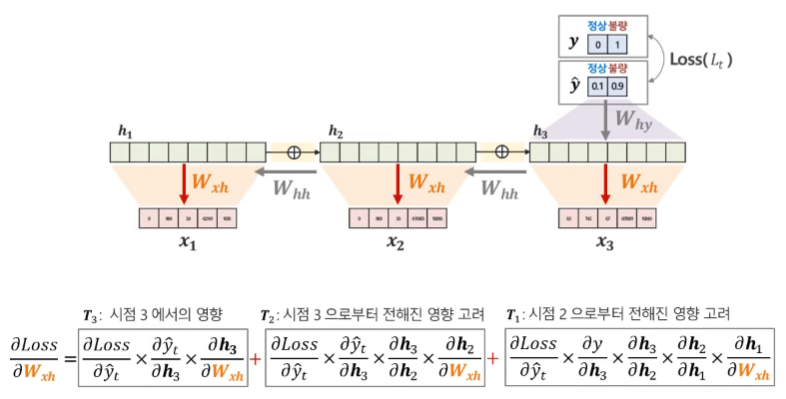
Parameter Update(학습)
이제 마지막으로 파라미터 값들을 업데이트한다. 여기서 업데이트는 Loss 값을 줄이는 방향으로 BPTT를 통해 계산한 Gradient만큼 수행하게되며, 이를 Gradient Descent 방법이라고 한다. 여기에 추가적으로 학습률(learning rate), 즉 Gradient에 곱해 얼만큼 이를 반영할 것인지를 결정하여 파라미터를 업데이트한다.

순환신경망 한계점
순환신경망은 장기 의존성 문제(long-term dependency problem)가 발생한다. 이는 Sequence의 길이가 길어질수록, 과거 정보의 학습에 어려움이 발생한다는 것이다. 이는 기울기 소실(vanishing gradient) 때문에 발생하는데, 이로 인해 장기 과거 시점에 대한 모델 파라미터의 업데이트가 되지 않고, 이로 인해 장기 과거 시점에 대한 모델 학습이 되지 않는다. 이러한 기울기 소실이 발생하는 이유는 Gradient의 계산 방식 때문이다. 먼저, 시점이 100개가되는 데이터를 예로 들면 W_hh에 대한 Gradient를 계산하는 과정에서 장기 과거 시점으로 갈수록 hidden state를 hidden state로 나누는 값을 곱하는 형태가 매우 많아지게 된다.

여기서 hidden state는 하이퍼볼릭 탄젠트를 활성화 함수로 사용하는데, 하이퍼볼릭 탄젠트의 미분 값은 다음 그래프와 같이 0부터 1사이의 값을 가지게 된다. 따라서 0부터 1 사이의 값을 갖는 값들을 계속해서 곱하게 되면 Gradient가 점점 0에 가까워져 파라미터의 업데이트가 되지 않는다는 것이다.
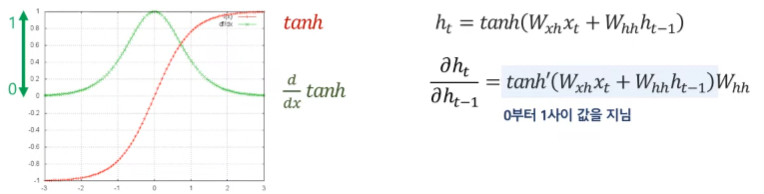
Long Short-Term Memory(LSTM)
Long Short Term Memory(LSTM)은 장기 의존성 문제를 완화한 RNN 개선 모델이다. LSTM은 RNN에는 없었던 cell state 구조를 제안하고, 3가지 gate를 추가한 구조이다. 여기서 활용되는 gate는 Forget gate, Input gate, Output gate이다. 이 gate는 hidden state와 같은 벡터 형태라고 생각하면 된다. 여기서 RNN과 LSTM을 비교하기 위해 모델을 회로도 형태로 표현하면 다음과 같다. 두 모델 모두 가장 중요한 것은 결국 hidden state h_t를 계산하여 W_hy와의 가중합을 통해 예측 값을 생성하는 것이다. 대신 LSTM은 기존에 없던 3가지 gate를 통해 cell state, hidden state를 업데이트한다. 참고로 3가지의 gate 및 cell state, hidden state 모두 vector이다.
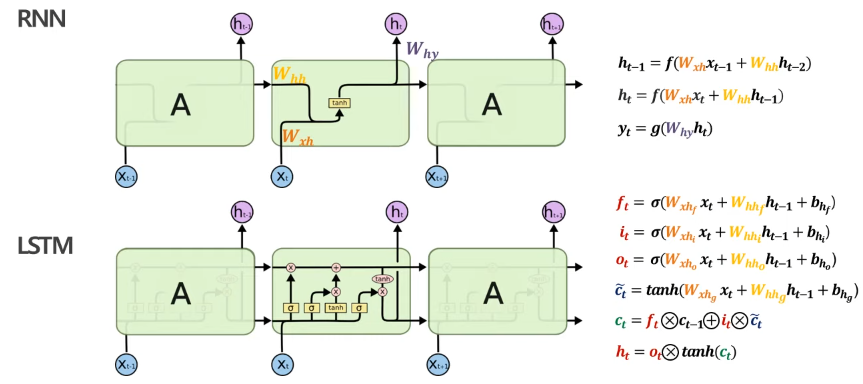
LSTM에선 hidden state와 cell state를 업데이트하기 위해 3가지 값을 계산해야 한다.
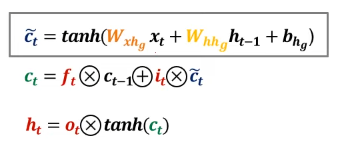
이 3가지의 값들을 계산하는 방법을 회로도로 표시하면 다음과 같다.
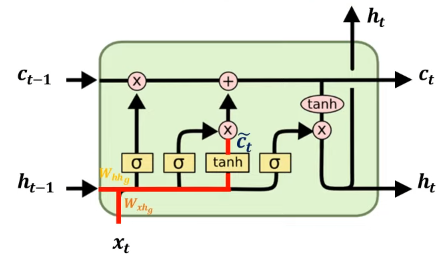
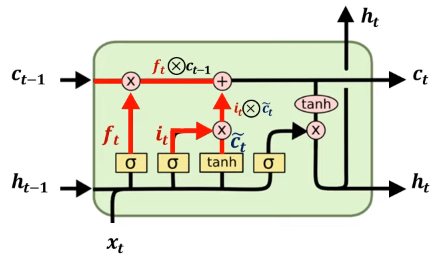
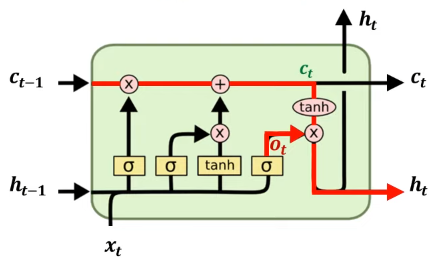
LSTM에서 hidden state를 업데이트하는 과정은 다음과 같다. 먼저 각 Gate 값을 계산한 후에 Cell state를 업데이트 하고, 최종적으로 hidden state를 업데이트한다.
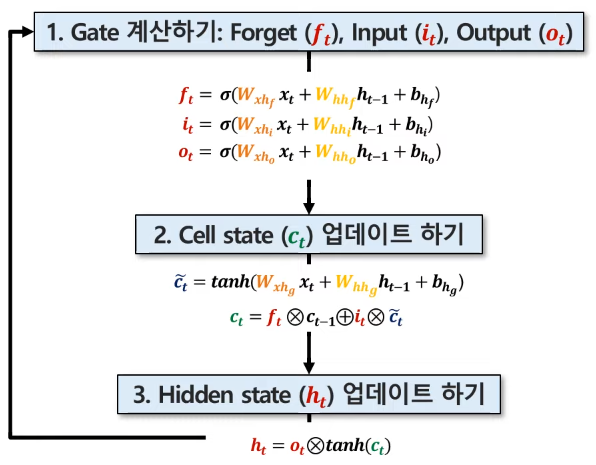
Gate 계산하기
Gate는 Sigmoid function 으로 정의되어 최종적으로 0~1 사이의 값을 가지는 벡터이다. 이는 최종적으로 얼마나 적용할 것인지에 대한 가중치 역할을 수행한다. 또한 Gate마다 서로 다른 파라미터(가중치)를 사용하기 때문에 서로 다른 값을 가지게 된다. 이 가중치는 학습을 통해 업데이트된다.
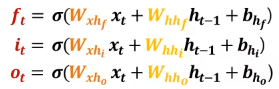
- Forget gate : 불필요한 과거 정보를 잊기 위한 gate
- 과거 cell state에서 사용하지 않을 데이터에 대한 가중치
- 과거 정보 c_t-1와의 합성곱을 통해 이 중 얼마만큼을 기억할 것인지에 대한 가중치(0~1 사이의 값)
- Input gate : 현재 정보를 기억하기 위한 gate
- cell state에서 사용할 데이터를 저장하기 위한 가중치
- 현재 정보를 나타내는 임시 cell state와의 합성곱을 통해 이 중 얼마만큼을 기억할 것인지에 대한 가중치
- Output gate : 어떤 정보를 output으로 내보질지 결정하기 위한 gate
- hidden state에 cell state를 얼마나 반영할 것인지에 대한 가중치
Cell state 업데이트 하기
cell state를 업데이트하기 위해선 먼저 임시 cell state를 생성해야 한다. 임시 cell state의 활성화 함수는 하이퍼볼릭 탄젠트이기 때문에 이 값은 -1~1 사이의 값을 가지는 벡터로 산출된다. 이는 수식적으로 RNN에서의 hidden state와 유사하다. 이후 임시 cell state와 forget gate, input gate를 활용하여 현 시점에 대한 cell state 값을 업데이트하게 된다.
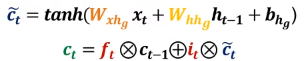
Hidden state 업데이트 하기
최종적으로 단기적 정보를 나타내는 hidden state를 업데이트한다. 앞서 계산한 cell state에 하이퍼볼릭 탄젠트를 실행한 후 가중치 역할을 수행하는 output gate와의 합성곱을 통해 hidden state를 계산한다. 이후 hidden state와 가중치 W_hy와의 곱을 통해 예측 값을 계산할 수 있다.

Gated Recurrent Unit(GRU)
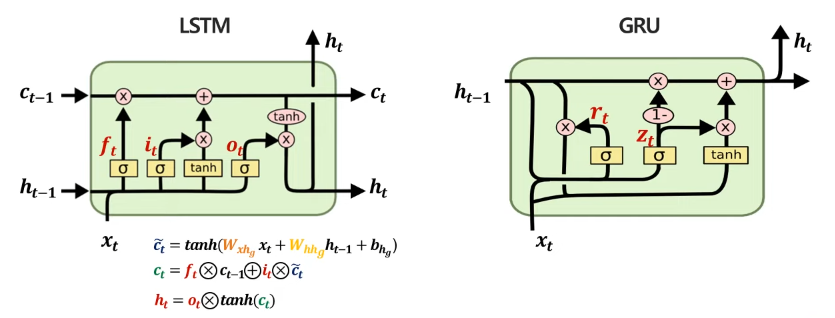
Gated Recurrent Unit(GRU)는 경량화된 LSTM 모델이라고 볼 수 있다. 일반적인 LSTM에서는 cell state와 3가지의 gate(forget, input, output)가 정의되는데, GRU는 LSTM의 forget gate, input gate를 update gate로 통합시켰으며, output gate를 없애고 reset gate를 정의했다. 또한 cell state와 hidden state를 hidden state로 통합하여 전체적으로 파라미터 개수를 줄였다. 이를 비교해보면 다음과 같다.
update gate, reset gate, 임시 cell state에 대한 계산 식은 다음과 같다.(cell state와 hidden state는 통합되서 표현하지만, 편의성을 위해 임시 cell state로 표현한다)
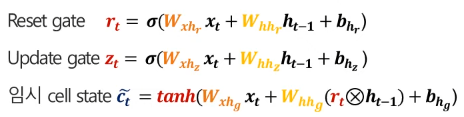
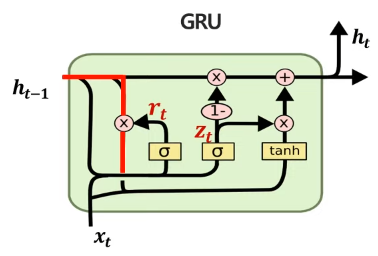
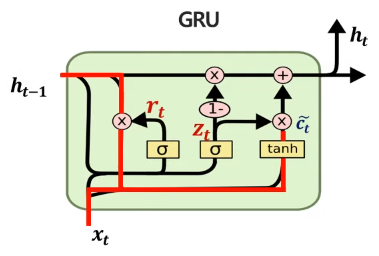
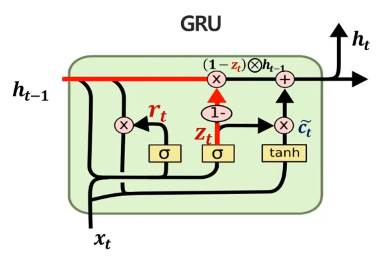

결론적으로 이들을 활용한 hidden state는 다음과 같이 계산할 수 있다. 과거 정보에 대한 가중치는 (1-update gate)의 가중치를 두고 기존 LSTM에서 cell state를 활용한 것과 달리 h_t-1, 즉 과거 hidden state를 활용하여 계산하고, 현재 정보에 대해선 update gate 만큼의 가중치를 두어 hidden state를 계산한다. 결국 궁극적으로 hidden state를 계산하기 위해 과거 정보와 현재 정보를 가중치를 두어 계산하는 틀은 동일하지만, 좀 더 단순화된 방법으로 계산이 가능하다.
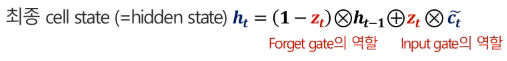
이 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 듣고 작성한 글입니다.
(이미지 출처 : 핵심 머신러닝)
순환 신경망 학습
학습이란 데이터를 통해 parameters를 추정한다는 것을 의미한다. 순환 신경망은 t시점까지의 과거 정보를 활용하여 y를 예측하게 되는데, 학습 대상이 되는 파라미터는 3가지이다. 첫 번째는 t 시점의 데이터를 반영한 W_xh 가중치, 두 번째는 t 시점 이전의 정보를 반영하는 W_hh 가중치, 그리고 t 시점의 y를 예측할 때 활용하는 W_hy 가중치이다. 해당 파라미터는 매 시점마다 공유하는 구조이며(parameter sharing), 매 시점 파라미터를 구성하는 값이 같다. 또한 최적의 W는 W를 매 시점 적용했을 때 Loss가 최소가 되는 W이다. hidden state와 예측값은 다음과 같이 계산된다.
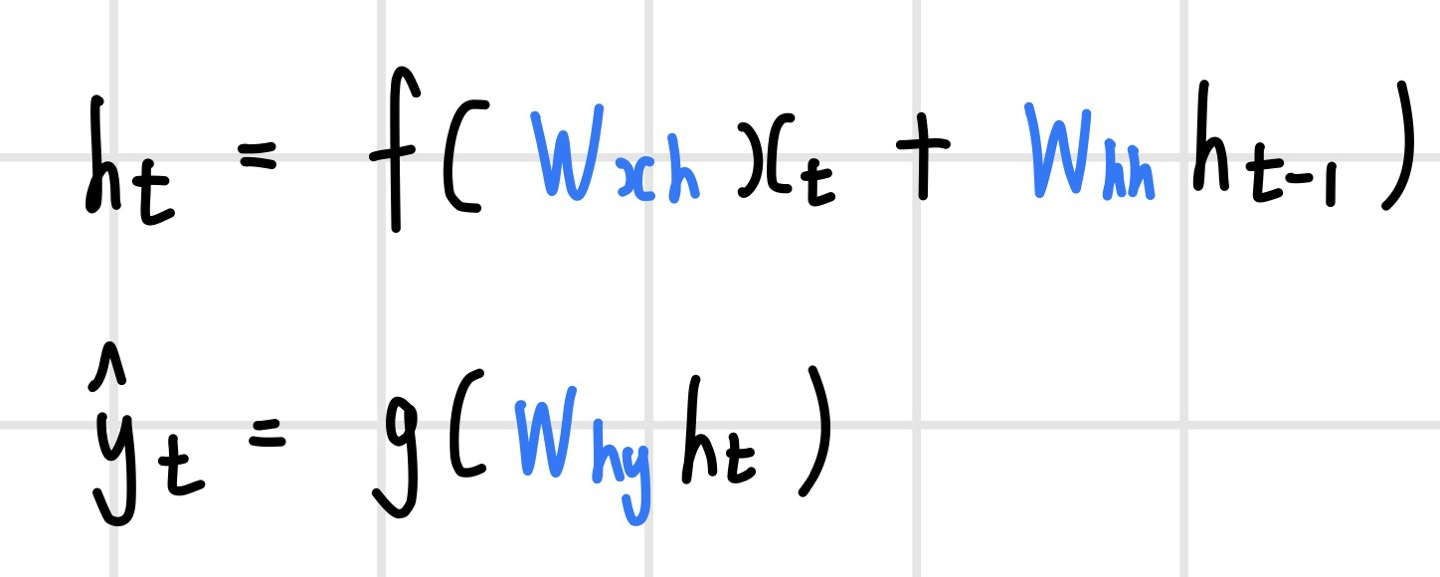
순환 신경망이 3가지의 가중치를 추론하는 학습과정은 다음과 같다.

Loss 계산하기 : Forward propagation
먼저 첫 번째로 Forward propagation, 즉 Loss 값을 계산하는 과정이다. hidden state h_t와 예측값, loss 값의 계산 방법은 다음과 같다. 여기서는 output이 1개인 경우를 고려했다.

만약 one to many, many to many처럼 output이 많은 경우의 Loss 값은 각 시점별 loss의 평균을 전체 Loss로 활용한다.

Gradient 계산하기 : backward propagation
RNN에서는 backward propagation 과정을 Backward Propagation Through Time, BPTT를 통해 수행한다. 역전파 과정이란 결국 Loss 값을 최소로 해주는 Gradient를 계산하여 파라미터를 업데이트하는 과정에 더해주거나 빼주는 과정을 말한다. 먼저 W_hy의 Gradient를 계산하는 방법은 다음과 같다. Loss를 해당 가중치로 바로 미분하는 것이 어렵기 때문에 chain rule을 활용하여 미분을 수행한다.

다음으론 W_hh 파라미터에 대한 Gradient를 계산하는 과정이다. W_hh의 경우 여러 시점에 있는 파라미터이기 때문에 모든 시점을 고려해야 한다. 만약 3번째 시점까지 데이터가 존재한다면 1번째, 2번째, 3번째 시점의 Gradient를 모두 계산해 더해주어야 한다.

마지막으로 W_xh 또한 각 시점마다 나타나는 가중치이기 때문에, 모든 시점을 고려하여 Gradient를 계산해주어야 한다.

Parameter Update(학습)
이제 마지막으로 파라미터 값들을 업데이트한다. 여기서 업데이트는 Loss 값을 줄이는 방향으로 BPTT를 통해 계산한 Gradient만큼 수행하게되며, 이를 Gradient Descent 방법이라고 한다. 여기에 추가적으로 학습률(learning rate), 즉 Gradient에 곱해 얼만큼 이를 반영할 것인지를 결정하여 파라미터를 업데이트한다.

순환신경망 한계점
순환신경망은 장기 의존성 문제(long-term dependency problem)가 발생한다. 이는 Sequence의 길이가 길어질수록, 과거 정보의 학습에 어려움이 발생한다는 것이다. 이는 기울기 소실(vanishing gradient) 때문에 발생하는데, 이로 인해 장기 과거 시점에 대한 모델 파라미터의 업데이트가 되지 않고, 이로 인해 장기 과거 시점에 대한 모델 학습이 되지 않는다. 이러한 기울기 소실이 발생하는 이유는 Gradient의 계산 방식 때문이다. 먼저, 시점이 100개가되는 데이터를 예로 들면 W_hh에 대한 Gradient를 계산하는 과정에서 장기 과거 시점으로 갈수록 hidden state를 hidden state로 나누는 값을 곱하는 형태가 매우 많아지게 된다.

여기서 hidden state는 하이퍼볼릭 탄젠트를 활성화 함수로 사용하는데, 하이퍼볼릭 탄젠트의 미분 값은 다음 그래프와 같이 0부터 1사이의 값을 가지게 된다. 따라서 0부터 1 사이의 값을 갖는 값들을 계속해서 곱하게 되면 Gradient가 점점 0에 가까워져 파라미터의 업데이트가 되지 않는다는 것이다.
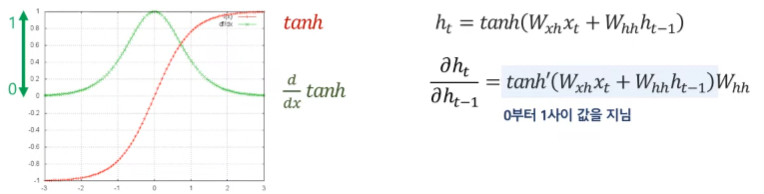
Long Short-Term Memory(LSTM)
Long Short Term Memory(LSTM)은 장기 의존성 문제를 완화한 RNN 개선 모델이다. LSTM은 RNN에는 없었던 cell state 구조를 제안하고, 3가지 gate를 추가한 구조이다. 여기서 활용되는 gate는 Forget gate, Input gate, Output gate이다. 이 gate는 hidden state와 같은 벡터 형태라고 생각하면 된다. 여기서 RNN과 LSTM을 비교하기 위해 모델을 회로도 형태로 표현하면 다음과 같다. 두 모델 모두 가장 중요한 것은 결국 hidden state h_t를 계산하여 W_hy와의 가중합을 통해 예측 값을 생성하는 것이다. 대신 LSTM은 기존에 없던 3가지 gate를 통해 cell state, hidden state를 업데이트한다. 참고로 3가지의 gate 및 cell state, hidden state 모두 vector이다.

LSTM에선 hidden state와 cell state를 업데이트하기 위해 3가지 값을 계산해야 한다.
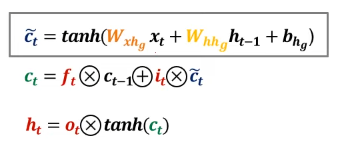
이 3가지의 값들을 계산하는 방법을 회로도로 표시하면 다음과 같다.



LSTM에서 hidden state를 업데이트하는 과정은 다음과 같다. 먼저 각 Gate 값을 계산한 후에 Cell state를 업데이트 하고, 최종적으로 hidden state를 업데이트한다.

Gate 계산하기
Gate는 Sigmoid function 으로 정의되어 최종적으로 0~1 사이의 값을 가지는 벡터이다. 이는 최종적으로 얼마나 적용할 것인지에 대한 가중치 역할을 수행한다. 또한 Gate마다 서로 다른 파라미터(가중치)를 사용하기 때문에 서로 다른 값을 가지게 된다. 이 가중치는 학습을 통해 업데이트된다.
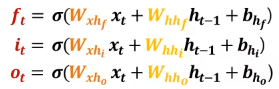
- Forget gate : 불필요한 과거 정보를 잊기 위한 gate
- 과거 cell state에서 사용하지 않을 데이터에 대한 가중치
- 과거 정보 c_t-1와의 합성곱을 통해 이 중 얼마만큼을 기억할 것인지에 대한 가중치(0~1 사이의 값)
- Input gate : 현재 정보를 기억하기 위한 gate
- cell state에서 사용할 데이터를 저장하기 위한 가중치
- 현재 정보를 나타내는 임시 cell state와의 합성곱을 통해 이 중 얼마만큼을 기억할 것인지에 대한 가중치
- Output gate : 어떤 정보를 output으로 내보질지 결정하기 위한 gate
- hidden state에 cell state를 얼마나 반영할 것인지에 대한 가중치
Cell state 업데이트 하기
cell state를 업데이트하기 위해선 먼저 임시 cell state를 생성해야 한다. 임시 cell state의 활성화 함수는 하이퍼볼릭 탄젠트이기 때문에 이 값은 -1~1 사이의 값을 가지는 벡터로 산출된다. 이는 수식적으로 RNN에서의 hidden state와 유사하다. 이후 임시 cell state와 forget gate, input gate를 활용하여 현 시점에 대한 cell state 값을 업데이트하게 된다.
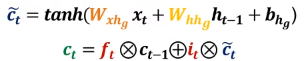
Hidden state 업데이트 하기
최종적으로 단기적 정보를 나타내는 hidden state를 업데이트한다. 앞서 계산한 cell state에 하이퍼볼릭 탄젠트를 실행한 후 가중치 역할을 수행하는 output gate와의 합성곱을 통해 hidden state를 계산한다. 이후 hidden state와 가중치 W_hy와의 곱을 통해 예측 값을 계산할 수 있다.

Gated Recurrent Unit(GRU)
Gated Recurrent Unit(GRU)는 경량화된 LSTM 모델이라고 볼 수 있다. 일반적인 LSTM에서는 cell state와 3가지의 gate(forget, input, output)가 정의되는데, GRU는 LSTM의 forget gate, input gate를 update gate로 통합시켰으며, output gate를 없애고 reset gate를 정의했다. 또한 cell state와 hidden state를 hidden state로 통합하여 전체적으로 파라미터 개수를 줄였다. 이를 비교해보면 다음과 같다.

update gate, reset gate, 임시 cell state에 대한 계산 식은 다음과 같다.(cell state와 hidden state는 통합되서 표현하지만, 편의성을 위해 임시 cell state로 표현한다)
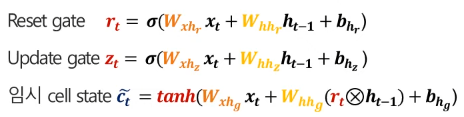




결론적으로 이들을 활용한 hidden state는 다음과 같이 계산할 수 있다. 과거 정보에 대한 가중치는 (1-update gate)의 가중치를 두고 기존 LSTM에서 cell state를 활용한 것과 달리 h_t-1, 즉 과거 hidden state를 활용하여 계산하고, 현재 정보에 대해선 update gate 만큼의 가중치를 두어 hidden state를 계산한다. 결국 궁극적으로 hidden state를 계산하기 위해 과거 정보와 현재 정보를 가중치를 두어 계산하는 틀은 동일하지만, 좀 더 단순화된 방법으로 계산이 가능하다.
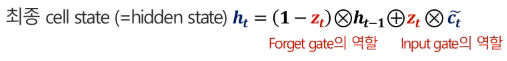
이 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 듣고 작성한 글입니다.
(이미지 출처 : 핵심 머신러닝)