기억을 갖는 신경망 모델 RNN
기억을 전달하는 순환 신경망
시간과 공간적 순서 관계가 있는 데이터를 `순차 데이터(sequence data)`라고 부른다. 순차 데이터는 시공간의 순서 관계로 형성되는 문맥 또는 `콘텍스트(context)`를 갖는다. 현재 데이터를 이해할 때 앞뒤에 있는 데이터를 함께 살펴보면서 콘텍스트를 파악해야 현재 데이터의 역할을 이해할 수 있다. 인공 신경망이 데이터의 순서를 고려하여 콘텍스트를 만들려면 데이터의 순차 구조를 인식할 수 있어야 하고, 데이터의 콘텍스트 범위가 넓더라도 처리할 수 있어야 한다. 이런 점들을 고려하여 만든 인공 신경망이 바로 `순환 신경망(RNN: Recurrent Neural Network)`이다.
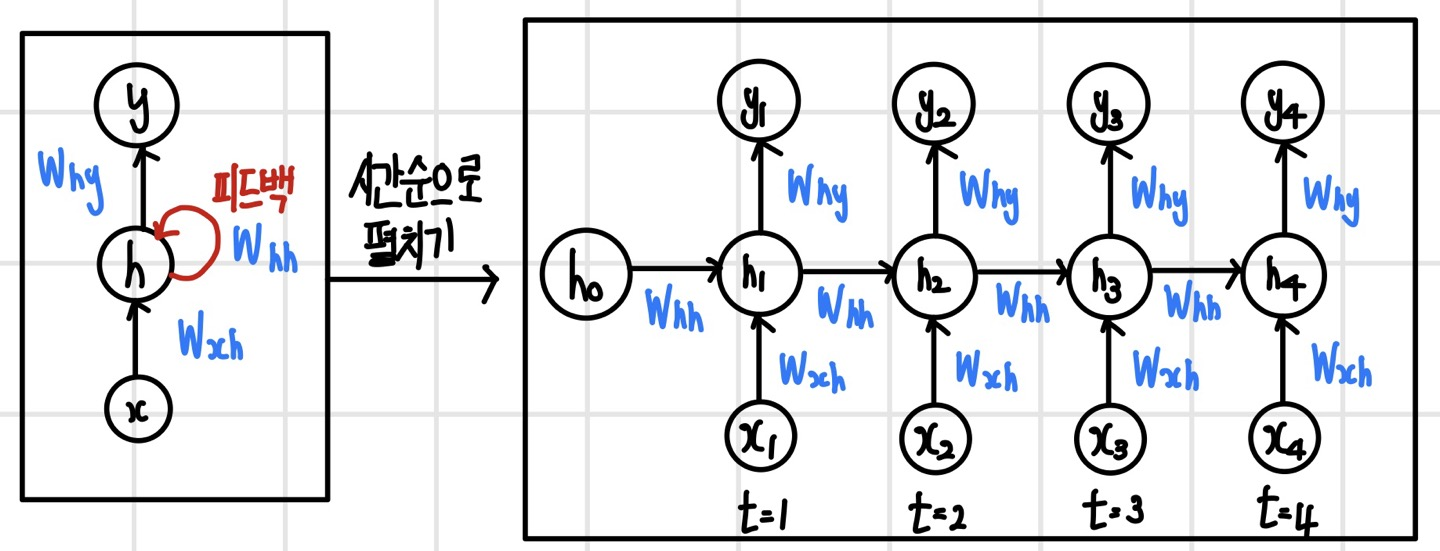
순방향 신경망이나 컨벌루션 신경망과는 다르게 순환 신경망은 데이터의 순차 구조를 인식하기 위해 데이터를 시간 순서대로 하나씩 입력받는다. 이후 순서대로 입력받은 데이터의 컨텍스트를 만들기 위해 은닉 계층에 피드백 연결을 가진다. 다음 그림은 기본 순환 신경망 모델이다.

기본적으로 모델은 입력 계층, 은닉 계층, 출력 계층으로 이루어지며 은닉 계층은 여러 계층이 될 수 있다. 그러나 일반적으로 순환 신경망은 은닉 계층을 깊게 쌓아도 성능이 크게 향상하지 않는 경우가 많아 보통 한 두 계층 이내로 쌓는다. 각 시간 단계에서 데이터가 처리되는 과정은 입력 계층, 은닉 계층, 출력 계층 순서대로 실행된다. 한 가지 차이점은 은닉 계층에 피드백 연결이 있기 때문에 은닉 상태가 다음 단계로 전달된다는 점이다. 여기서 은닉 상태는 '은닉 계층의 출력'을 말한다. 이 은닉 상태에는 '시간 단계별로 입력된 데이터가 순차적으로 추상화되어 형성된 콘텍스트'를 저장한다. 여기에 피드백 연결은 시간의 흐름에 따라 콘텍스트를 기억하는 과정으로 생각할 수 있다.
순환 연산 방식
초기 은닉 상태 h0는 영벡터라고 가정하고 각 단계를 변수 t(t>=1)로 표현하면 순환 신경망의 순환 연산은 다음의 순서로 실행된다.

기본 순환 신경망 모델(Vanilla RNN)
함수 f가 다음과 같은 형태로 정의되는 신경망을 `기본 순환 신경망 모델(Vanilla RNN)`이라고 한다.
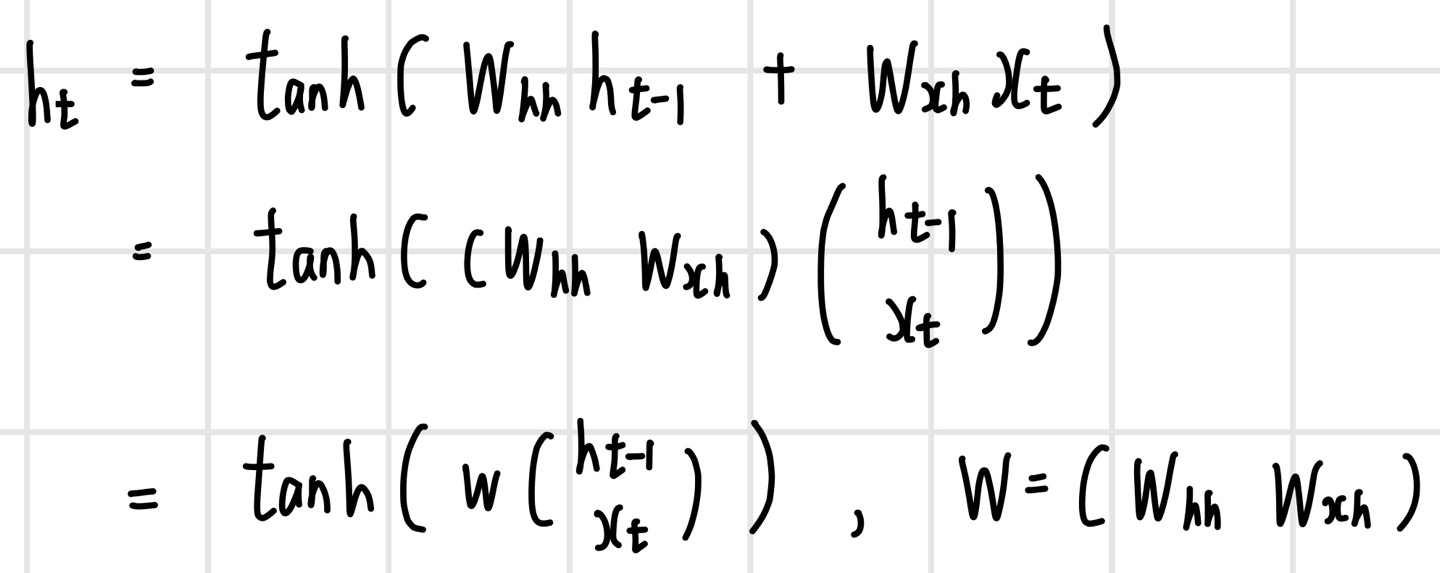
기본 순환 신경망에는 3가지의 가중치가 있으며, 다음과 같은 구조로 되어있다. 순환 신경망의 가중치는 모든 시간 단계에서 공유되며, 기본 순환 신경망의 은닉 계층은 입력과 가중치를 가중 합산한 뒤 `하이퍼볼릭 탄젠트`를 실행한다.

순환 신경망의 입력, 은닉 상태, 출력
순환 신경망의 입력과 은닉 상태는 무엇을 표현할까?
초기 은닉 상태인 h0를 영벡터라 가정했을 때 각 단계에서의 은닉 계층의 연산을 나열하면 다음과 같다. 즉, 은닉 상태는 지금까지 입력된 모든 데이터가 추상화되어 있다.

순환 신경망은 데이터의 순차 구조를 어떻게 포착할까?
은닉 계층은 '이전 상태, 새로운 입력'을 입력받아서 현재 상태를 매핑하는 함수이다. 은닉 계층의 식을 h0까지 전개해 보면 다음과 같이 표현된다. 이 식은 함수 f에 x1, x2, ..., xt가 순차적으로 입력되면서 추상화되는 과정을 보여준다. 따라서 은닉 계층을 나타내는 함수 f는 '추상화된 순차 구조를 한 단계 확장된 순창화된 순차 구조로 매핑하는 함수'이다.

순환 신경망의 출력 y는 무엇을 표현할까?
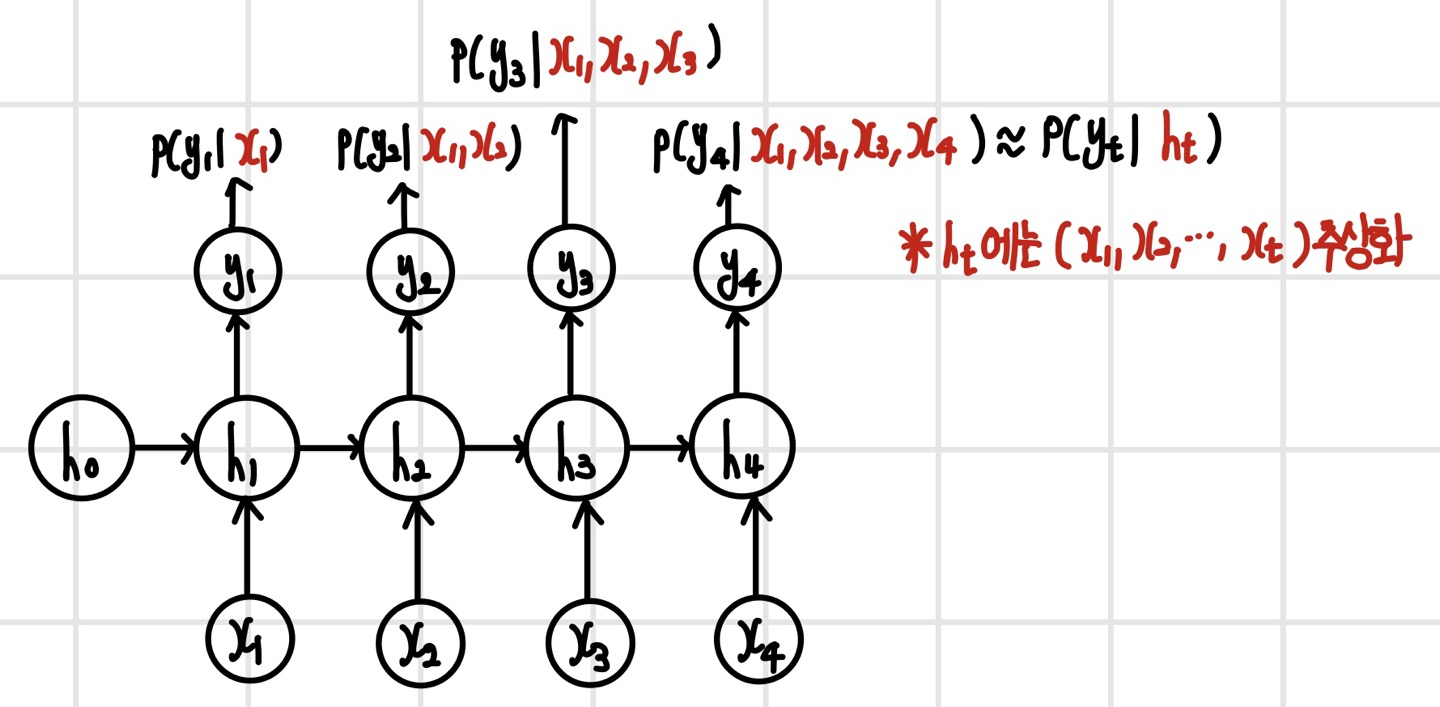
가중치 공유 효과
순환 신경망은 가중치를 모든 단계에서 공유하는데 그에 따른 이점은 다음과 같다.
- 데이터의 다양한 순차 구조를 하나의 가중치로 학습하기 때문에 특정 순차 구조가 어느 위치에서 나타나더라도 포착할 수 있다.
- 모든 단계가 같은 파라미터를 사용하므로 단계를 쉽게 추가할 수 있어 가변 길이 데이터를 유연하게 처리할 수 있다.
- 파라미터를 공유하면 파라미터 수가 절약되고, 정규화 효과가 생겨 비슷한 유형의 순차 패턴에 대한 일반화를 잘 할 수 있다.
순환 신경망의 주요 모델
순환 신경망은 입출력의 형태와 처리 방식에 따라 모델 구성이 다양하다.
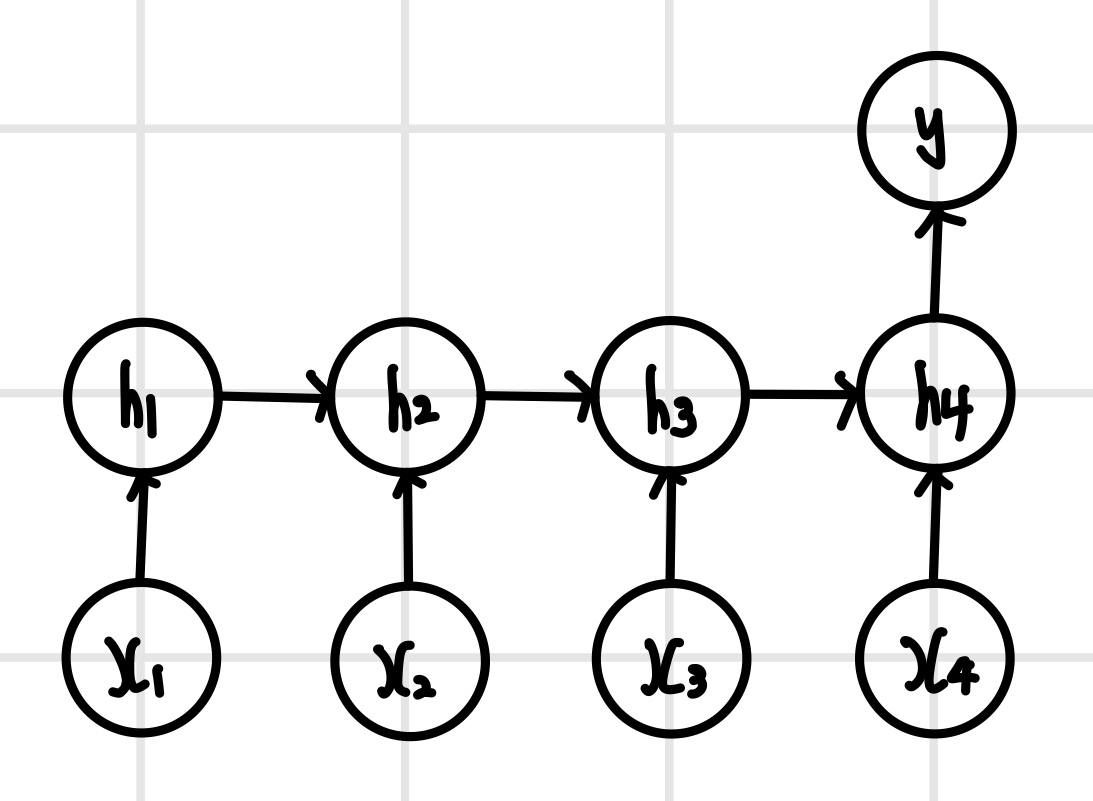
다대일(many-to-one) 모델
`다대일(many-to-one)` 모델은 입력은 순차열이지만 출력은 순차열이 아닐 때 사용하며, 모든 단계에서 입력을 받지만 출력은 마지막 단계에서만 한다. 예를 들어 영화 평론이 긍정적인지 부정적인지 `감성 분석(sentiment analysis)`을 할 때 주로 사용한다. 이는 영화 평론을 단어 단위로 분리해서 단계마다 단어를 입력하고, 영화 평론이 긍정인지 부정인지 여부는 마지막 단계에 출력한다.
다대다(many-to-many) 모델
`다대다(many-to-many)` 모델은 입출력이 길이가 같은 순차열일 때 사용하며, 모든 단계에서 입력을 받고 모든 단계에서 출력한다. 예를 들어 동영상을 프레임별로 분류한다면 단계별로 동영상 프레임을 입력해서 각 프레임을 분류한 결과를 출력한다. 다대다 모델에서 `티처 포싱(teacher forcing)` 방식으로 학습하면 학습이 안정화되고 수렴 속도도 빨라진다. 티처 포싱은 현재 단계의 출력을 다음 단계에 입력(지도 신호로 사용)하는 방법이다. 이때 훈련 시에는 모델의 예측 결과 대신 타깃을 직접 지도 신호로 사용해야 한다. 이는 훈련 중에는 모델이 정확한 예측을 할 수 없기 때문이다.
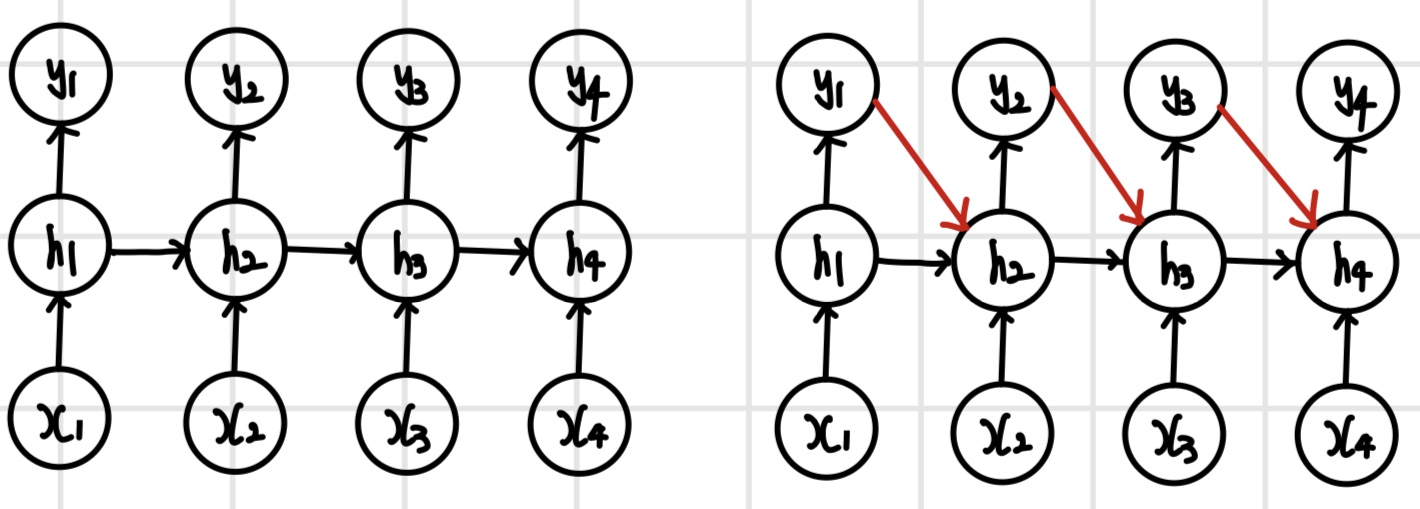
일대다(one-to-many) 모델
`일대다(one-to-many)` 모델은 입력은 순차열이 아니지만 출력은 순차열일 때 사용하며, 첫 번째 단계에서만 입력하고 모든 단계에서 출력한다. 예를 들어 이미지 캡션을 생성할 때 첫 번째 단계에서 이미지 컨텍스트를 입력하고 각 단계에서 이미지를 설명하는 문장의 단어를 순서대로 출력한다.
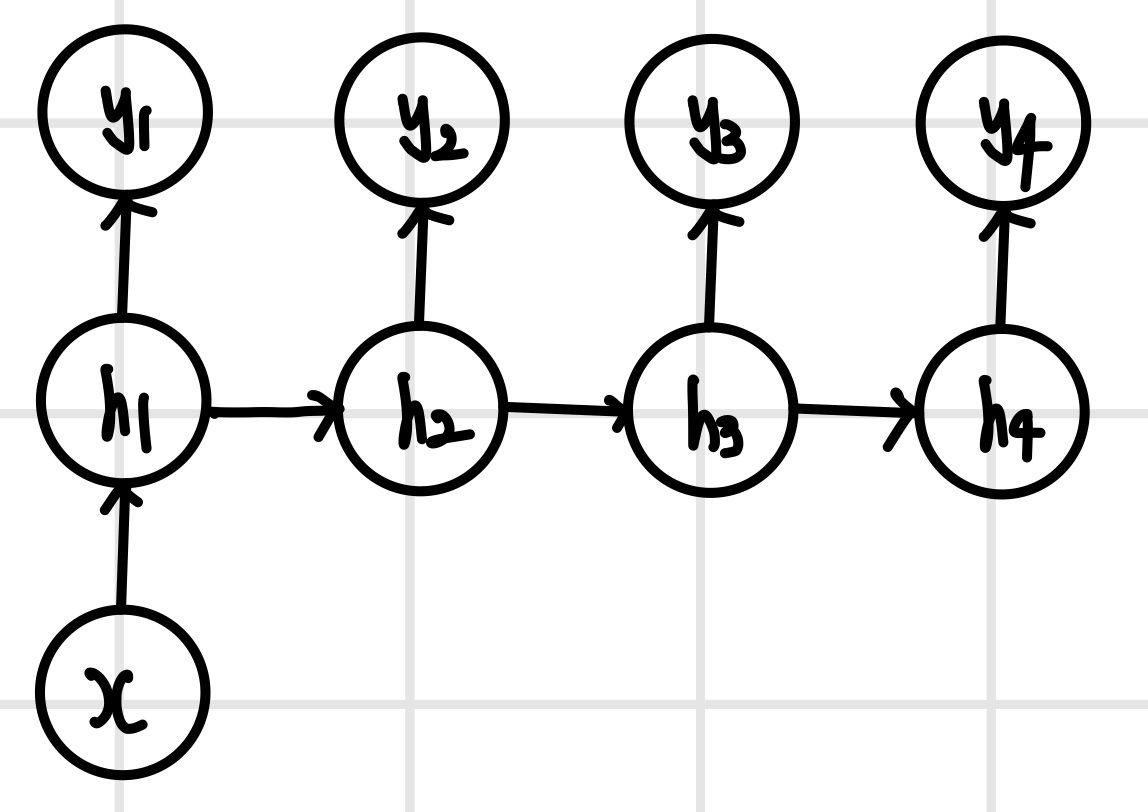
양방향(bidirectional) 모델
`양방향(bidirectional)` 모델은 입력을 양쪽으로 살펴보는 방식이다. 시간순으로 생성되는 데이터는 인과 관계에 따라 현재는 과거에만 의존하기 때문에 시간의 흐름 방향으로만 봐야 하지만, 공간적 순서 관계를 갖는 데이터는 상대적인 순서가 중요하므로 양방향으로 살펴보고 판단하는 것이 더 정확하다. 예를 들어 기계 번역을 할 때 문장을 순방향과 역방향 모두 보는 것이 더 좋은 번역 결과를 만든다. 양방향 모델은 입력 데이터를 순방향 계층과 역방향 계층에 모두 입력한다. 순방향 계층과 역방항 계층의 출력은 출력 계층에 입력되며, 출력 계층에서는 두 결과를 합쳐서 예측한다. 여기서 모델을 조금 변형해서 순방향 계층의 출력을 역방향 계층에 입력해서 처리하기도 한다. 이 경우 역방향 계층에서는 입력 데이터와 순방향 계층의 출력을 합쳐서 처리하고 그 결과를 출력 계층에 전달한다.
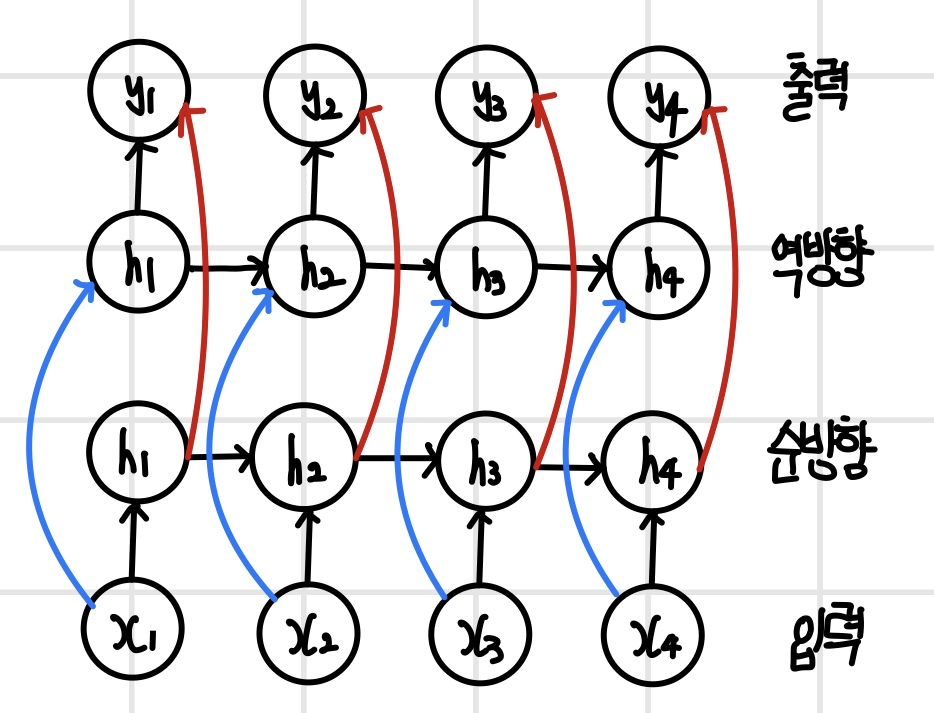
인코더-디코더(encoder-decoder) 모델
`인코더-디코더(encoder-decoder)` 모델은 입력과 출력의 길이가 서로 다른 순차열일 때 사용하며, 입력 데이터를 요약하는 인코더와 요약 데이터를 이용해서 출력 데이터를 생성하는 디코더로 구성된다. 순차열을 다른 순차열로 변환하여 `Seq2Seq(sequence-to-sequence)` 모델이라고도 부른다. 예를 들어 기계 번역과 같이 언어를 다른 언어로 변환하거나 오디오 데이터를 립싱크 동영상으로 변환할 때 사용한다. 인코더는 입력 데이터를 순차적으로 처리하다가 마지막 단계의 은닉 상태를 콘텍스트 벡터로 출력한다. 디코더는 인코더로부터 전달받은 콘텍스트 벡터를 모든 단계에 입력하고, 단계별로 예측하며 안정적인 학습을 하기 위해 티처 포싱을 적용한다.
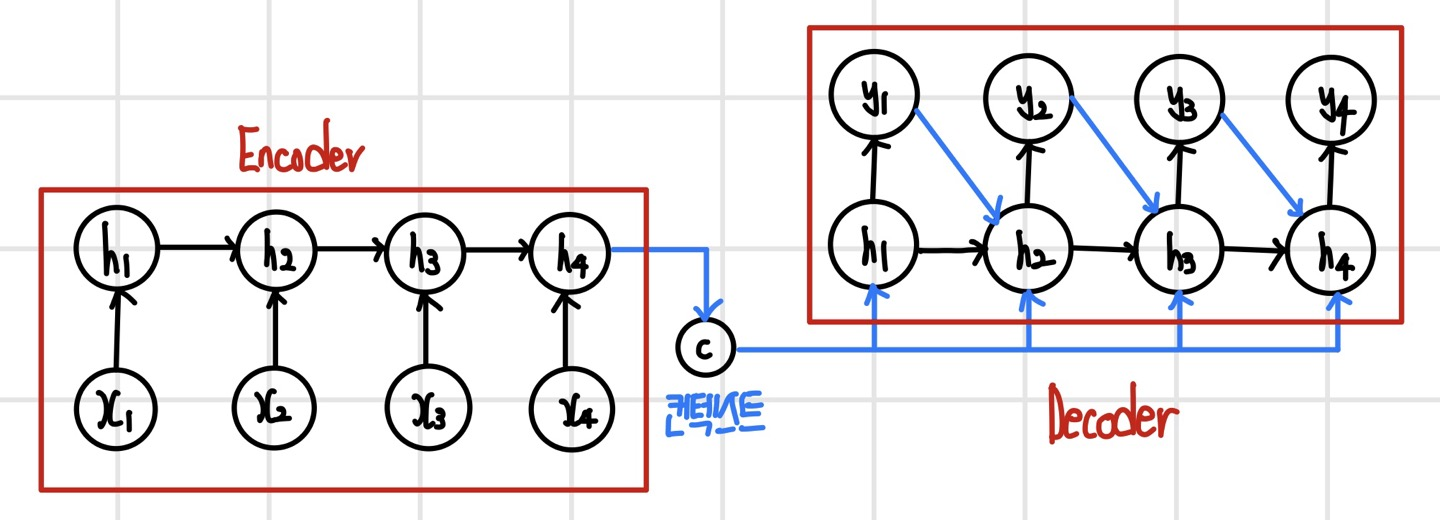
시간펼침 역전파(BPTT; backropagation through time)
순환 신경망을 시간 순서대로 펼쳐 놓으면 입력에서 출력까지 뉴런의 실행 순서가 정해지기 때문에 역전파 알고리즘은 이를 정확히 반대 순서로 수행하면 된다. 순환 신경망의 역전파는 시간 순서대로 펼쳐 놓은 상태에서 수행하기 때문에 `시간펼침 역전파(backpropagation through time)`으로 구분하며 `BPTT`라고 부른다.
순환 신경망의 손실 함수
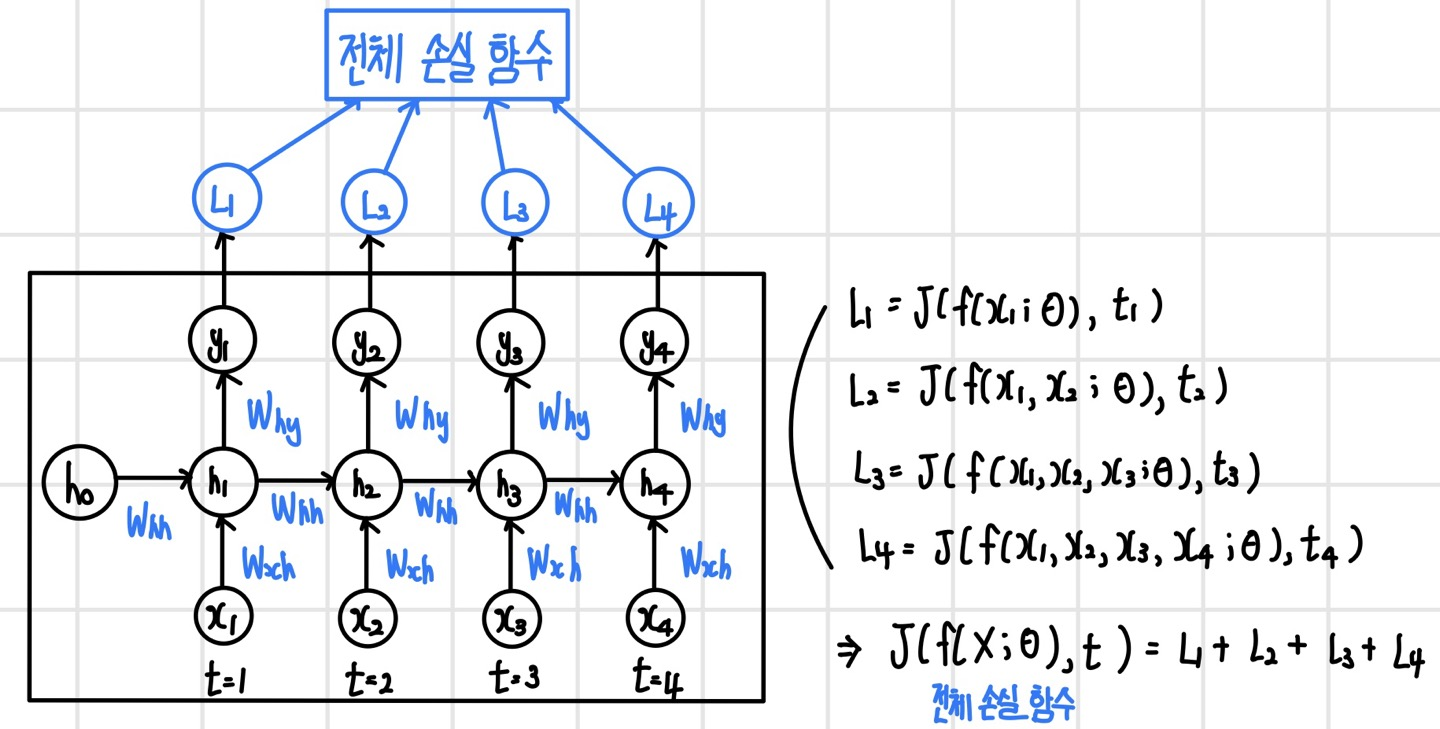
순환 신경망의 손실 함수 역시 시간 순서대로 펼쳐 놓은 상태에서 정의해야 하며 단계별로 출력하기 때문에 손실 함수 또한 단계별로 정의된다. 순환 신경망의 전체 손실 함수는 모든 단계의 손실 함수를 더해서 정의한다. 다음과 같이 입력 순차열이 X = (x1, x2, x3, x4)이고, 타깃 순차열이 t = (t1, t2, t3, t4)라고 하면 각 단계의 손실 L1, L2, L3, L4를 계산할 수 있다. 각 단계의 손실 함수는 회귀 문제의 경우 `MSE`, 분류 문제라면 `Cross Entropy`로 정의한다. 또한 전체 손실 함수는 각 단계의 손실 함수를 합한 값으로 정의한다.
시간펼침 역전파
마지막 단계의 출력 y4와 y3에 대한 역전파 순서를 빨간색 화살표로 표시하면 다음과 같다. 역전파가 전체 손실 함수에서 시작해서 y4를 지나 은닉 계층 h4에 도달하면, 시간의 역순으로 h4-h3-h2-h1 순서로 진행되면서 단계별로 은닉 계층에서 입력 계층으로 역전파가 분기된다. 역전파 과정에서 입력 계층과 은닉 계층 사이의 가중치와 피드백 연결에 있는 가중치가 업데이트되며, 가중치가 공유되므로 단계마다 같은 가중치가 업데이트된다.
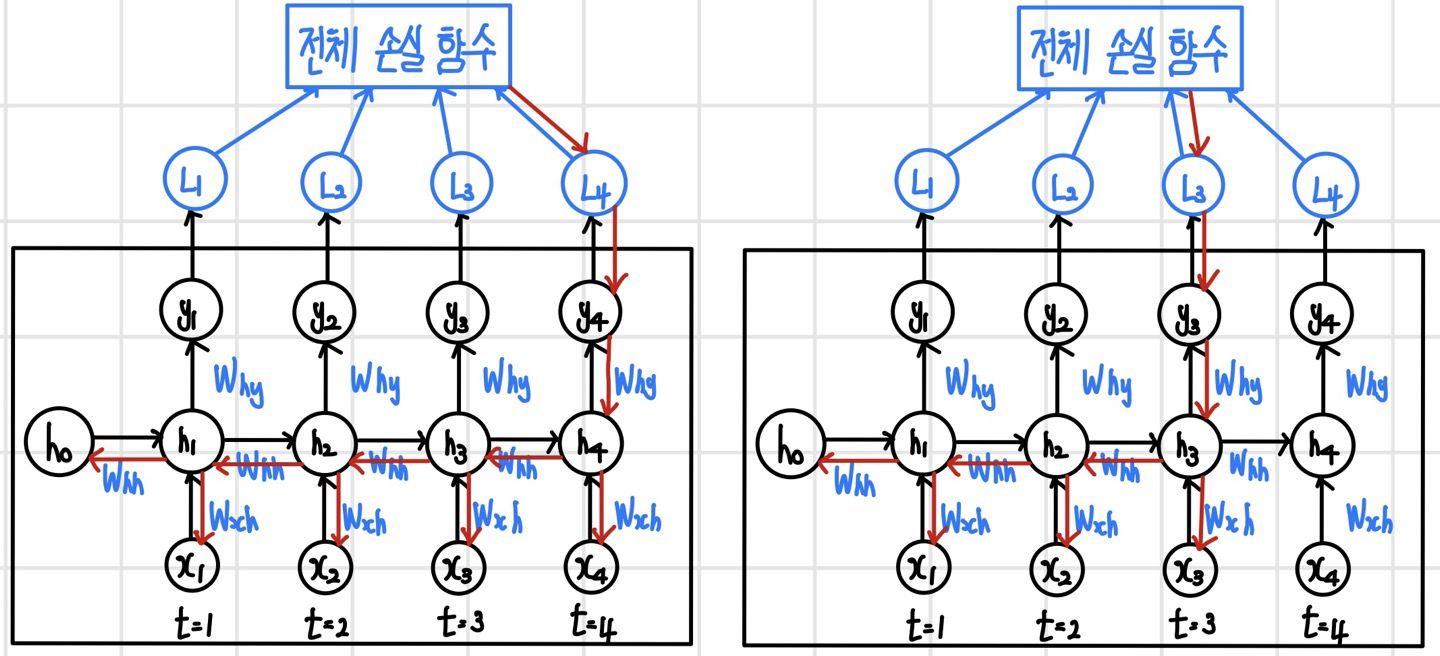
다음으로는 전체 손실 함수에서 역전파가 시작되어 모든 단계로 동시에 역전파되도록 시간펼침 역전파 알고리즘을 실행해 보면 다음과 같다. 전체 손실 함수에서 모든 은닉 계층까지는 역전파가 동시에 실행될 수 있지만, 은닉 계층부터는 순차적으로 실행될 수밖에 없다. 예를 들어 네 번째 단계의 역전파가 h3에 도달했을 때 y3에서 아직 오차가 전달되지 않았다면 기다렸다가 모든 방향의 역전파가 완료되었을 때 다음 단계로 진행한다. 따라서 역전파는 마지막 단계에서 시작해서 시간의 역순으로 단계별로 순차 진행한다.
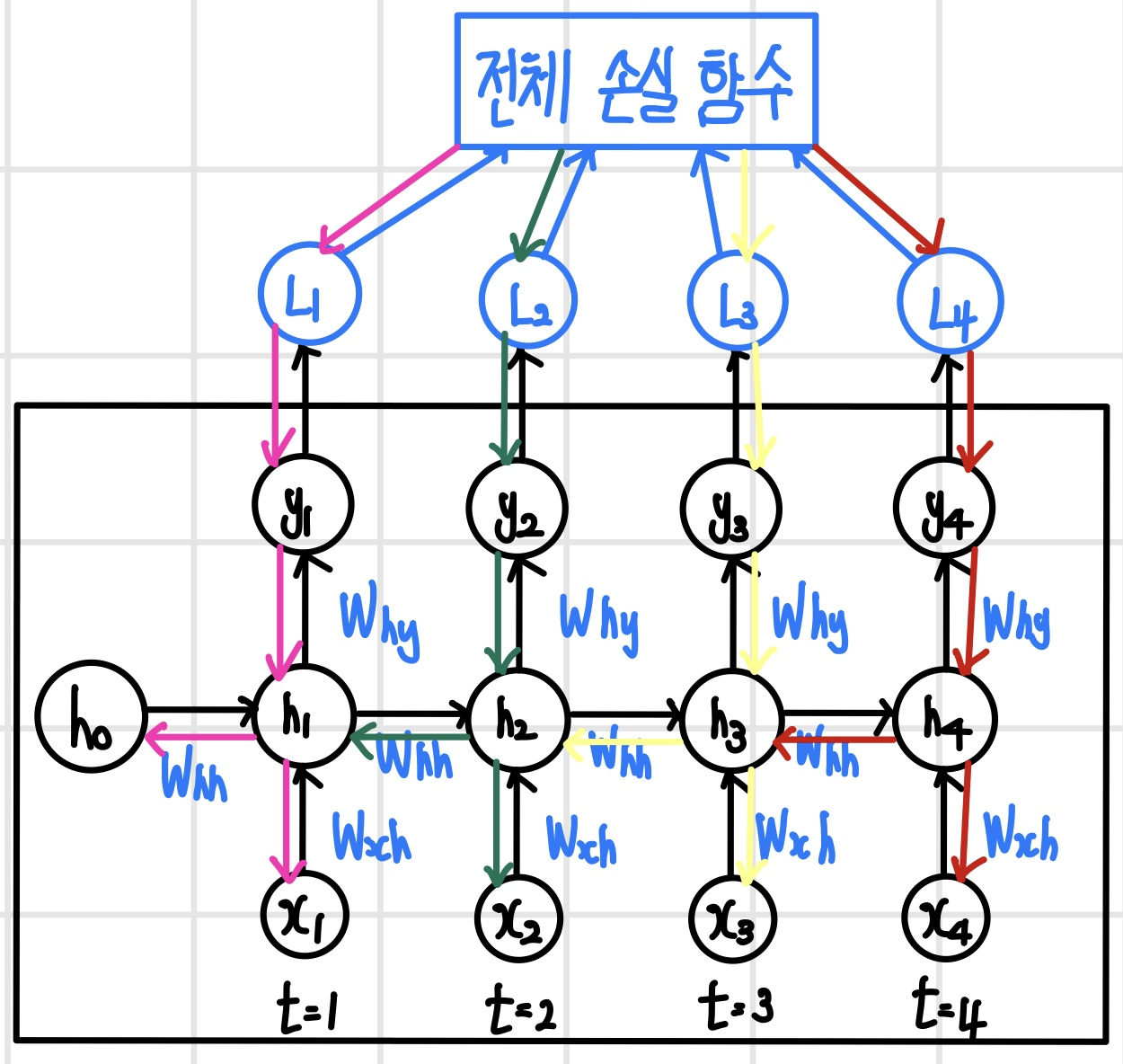
세 번째 단계의 은닉 계층 h3에서 역전파 알고리즘을 어떤 단계로 처리하는지 확인해보면 다음과 같다.

절단 시간펼침 역전파(truncated BPTT)
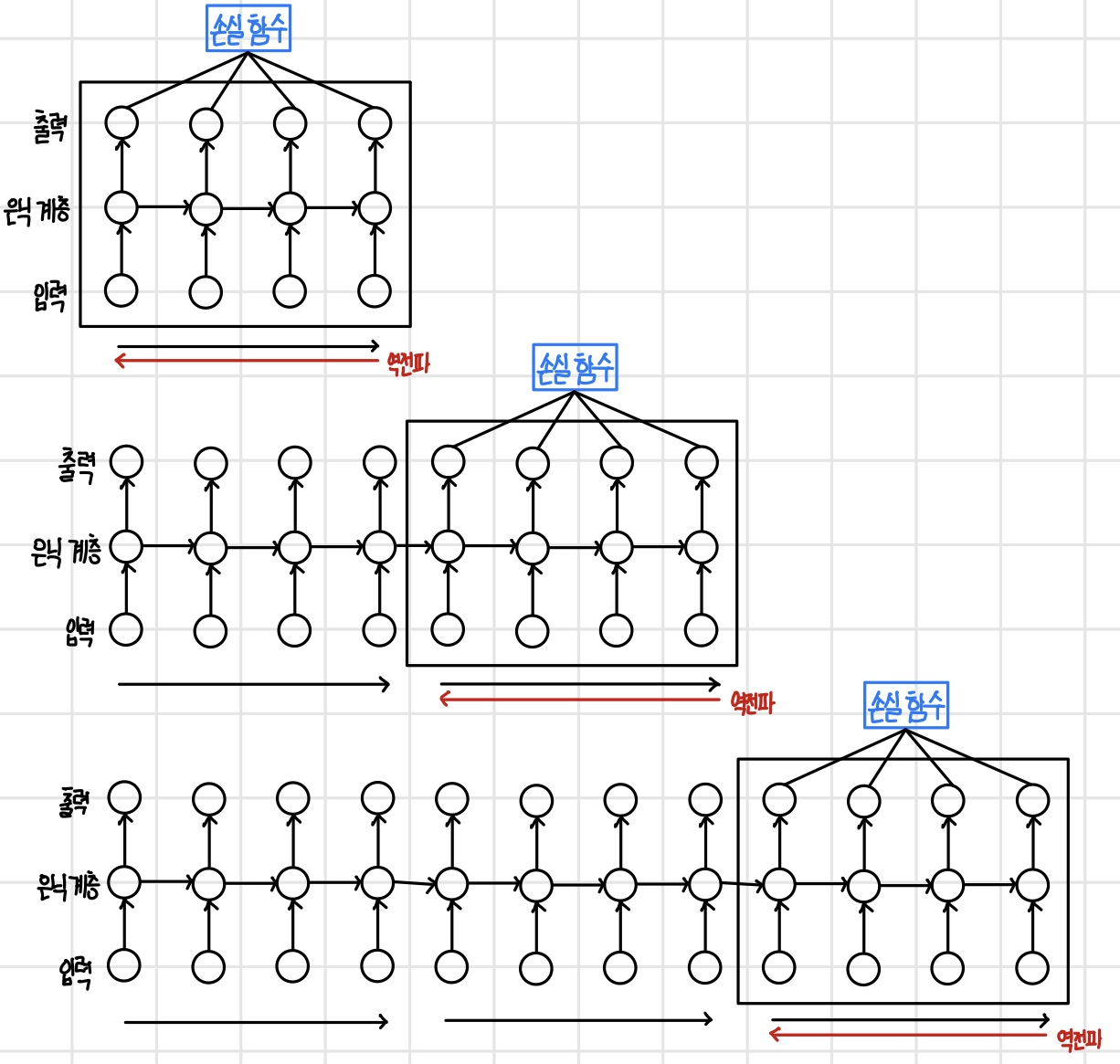
시간펼침 역전파 알고리즘은 마지막 단계를 실행한 뒤에 역전파를 하기 때문에 끝이 없는 순차열이나 아주 긴 순차열에는 적용할 수 없다. 이를 해결하기 위해 `절단 시간펼침 역전파(truncated BPTT)`는 일정 단계를 묶어서 순방향 진행을 하고 역전파를 실행하는 알고리즘이다. 이때 중요한 것은 첫 번째 묶음과 두 번째 묶음의 순차열이 연속적인 순차열이 되도록 만들어야 한다는 것이다. 역전파 과정에서 첫 번째 묶음의 마지막 은닉 상태를 기억해 두었다가 두 번째 묶음이 시작될 때 첫 번째 은닉 상태에 전달해 연속된 콘텍스트를 유지할 수 있다. 즉, 절단 시간펼침 역전파는 묶음 단위로 역전파를 하지만 묶음 간에 은닉 상태를 전달하여 연속된 콘텍스트를 갖게 함으로써 끝이 없는 순차열이나 매우 긴 순차열도 학습하게 해준다.

LSTM과 GRU
기본 순환 신경망(Vanilla RNN)은 최적화하기 어렵고, 성능적인 한계도 있다. 이런 점들을 극복하기 위해 `LSTM(Long Short-Trem Memory)`과 `GRU(Gated Recurrent Unit)`와 같은 셀 구조를 갖는 순환 신경망이 등장했다.
기본 순환 신경망의 문제점
`장기의존성(long-term dependency)` 문제는 콘텍스트 범위가 넓을 때 멀리 떨어진 입력에 대한 의존성이 있음에도 불구하고 입력의 영향이 점점 사라지는 현상을 말한다. 이 경우 순차열이 길어질수록 오래전에 입력된 데이터의 정보는 사라지기 때문에 정확한 예측을 할 수 없다. 이를 해결하려면 콘텍스트가 오래 지속하도록 구조를 변경해야 한다.
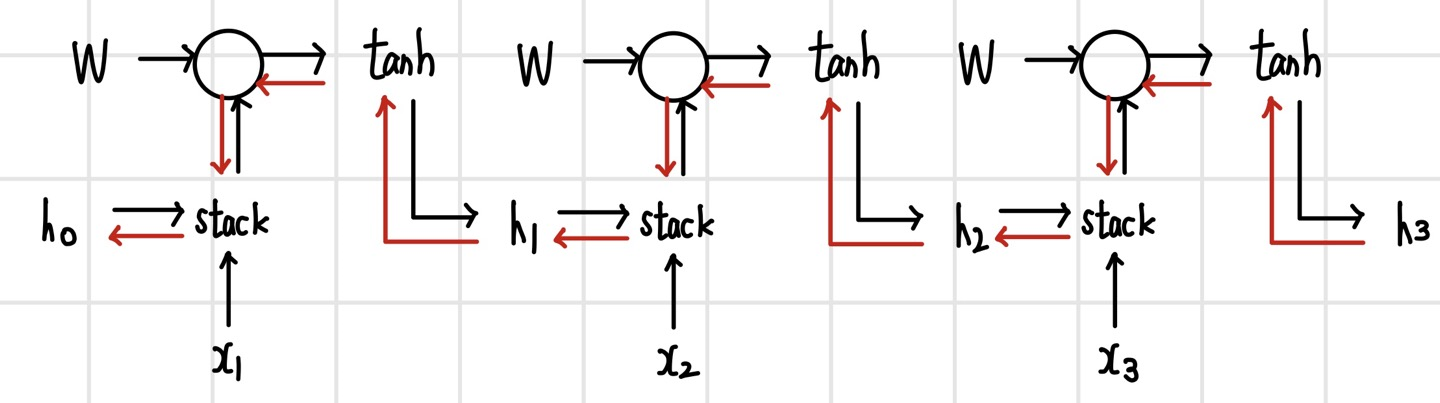
`그레이디언트 소실과 폭발(Gradient vanishing and exploding)` 문제는 학습하면서 그레이디언트가 없어지거나 발산하는 현상을 말한다. 기본 순환 신경망의 그레이디언트를 은닉 계층의 순방향 흐름은 검은색으로, 역방향의 그레이디언트 흐름은 빨간색으로 그렸다. 은닉 계층에서는 가중치 W와 입력을 가중 합산한 뒤에 하이퍼볼릭 탄젠트를 실행한다. 이러한 기본 순환 신경망이 여러 단계에 걸쳐 실행되면 은닉 계층의 단계마다 W가 곱해진다. 반대로 역전파를 할 때도 입력에 대한 지역 미분 W가 단계마다 곱해진다. 행렬이 반복적으로 곱해지면 행렬의 거듭제곱이 되기 때문에 각 차원의 고윳값 크기가 1보다 크면 발산하고, 고윳값 크기가 1보다 작으면 0으로 수렴한다. 기본 순환 신경망은 가중치 행렬 W가 반복적으로 곱해지는 형태 때문에 그레이디언트 소실과 폭발이 쉽게 일어난다.
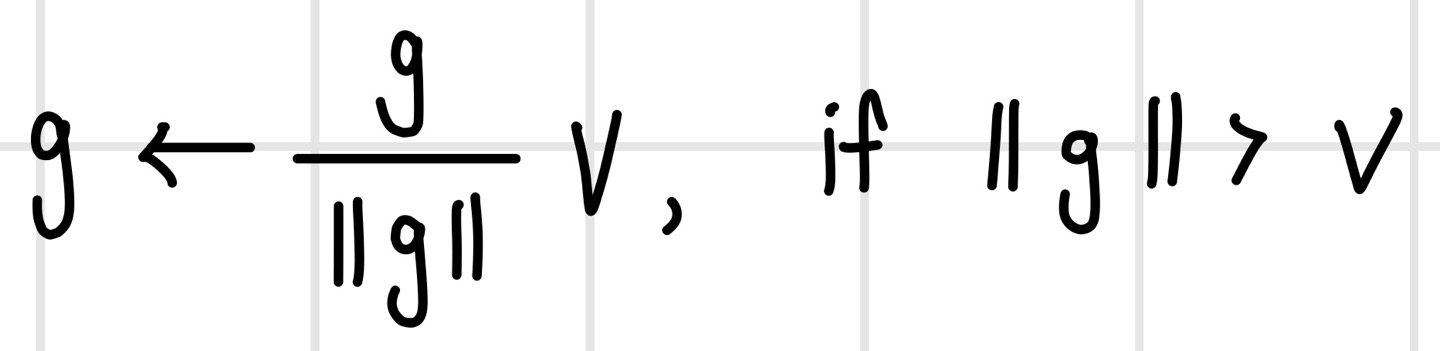
그레이디언트 폭발의 경우 `그레이디언트 클리핑(gradient clipping)`을 통해 그레이디언트가 일정 크기 이상으로 커지지 않게 하여 비교적 간단히 막을 수 있다. 그레이디언트가 g이고 임계치가 v라고 하면, 만일 g의 크기가 v보다 크다면 g를 단위 벡터로 만든 뒤에 v를 곱해 v와 같은 크기의 벡터로 만든다. 순환 신경망의 손실 곡면에 가파른 절벽이 나타나면 그레이디언트가 급격히 커져 엉뚱한 방향으로 가고 최적화 경로에서 크게 이탈하면서 최적화가 늦어지거나 잘 수행되지 않을 수 있다. 이때 그레이디언트 클리핑을 수행하면 보폭이 줄어들기 때문에 가파른 절벽을 만나도 경로를 이탈하지 않고 조금씩 전진하는 경로를 만들 수 있다.
LSTM(Long Term Short Memory)
`LSTM`은 그레이디언트 소실의 원인이 되는 가중치 W와의 행렬곱 연산이 그레이디언트 경로에 나타나지 않도록 구조를 변경한 모델이다.
그레이디언트 소실을 막는 모델 구조
LSTM은 셀 구조로 되어 있으며 셀에는 기본 순환 신경망에 있던 은닉 상태 ht 외에 `셀 상태(cell state)` Ct가 추가되었다. LSTM의 그레이디언트 흐름에서는 셀과 셀 사이에 두 상태를 연결하는 별도의 경로가 추가된다. 이 경로에는 가중치 W와의 행렬곱 연산이 없다. 이를 통해 순방향 및 역방향 흐름의 장기 의존성 문제와 그레이디언트 소실 문제를 완화한다. 반면 은닉 상태를 연결하는 경로에는 가중치 W와의 행렬곱 연산이 남아 있어 순차 데이터를 처리하는 뉴런 연산을 수행한다.
장기 기억과 단기 기억의 모델링
LSTM은 셀 상태에 오래 기억되는`장기 기억(long-term memory)`을 모델링하고, 은닉 상태는 `단기 기억(short-term memory)`으로 한정했다. 장기 기억은 오래 지속되지만 새로운 사건이 발생할 때마다 조금씩 강화하거나 약화하고 자주 사용하지 않으면 잊혀지기도 한다. 이를 위해 LSTM은 셀 상태를 W의 방해 없이 그대로 전달되는 구조로 설계했다. 새로운 사건이 발생하면 연관된 장기 기억 또는 단기 기억과 연합해서 인식하는 과정에서 단기 기억이 형성된다. 단기 기억은 최근에 일어난 사건은 빠르게 기억하지만, 상황이 전환되면 빠르게 잊혀지는 특성이 있다. 또한 같은 사건이 지속해서 반복되면 단기 기억은 장기 기억으로 전환되기도 한다. LSTM은 이러한 특성을 구성하기 위해 은닉 상태에 최근 사건에 대한 콘텍스트가 형성되도록 W가 곱해지는 구조로 설계했다.
장기 기억과 단기 기억의 상호작용
다음은 LSTM의 셀을 간단히 표현한 것이다. 이를 통해 장기 기억과 단기 기억이 서로 다음과 같이 상호작용한다.
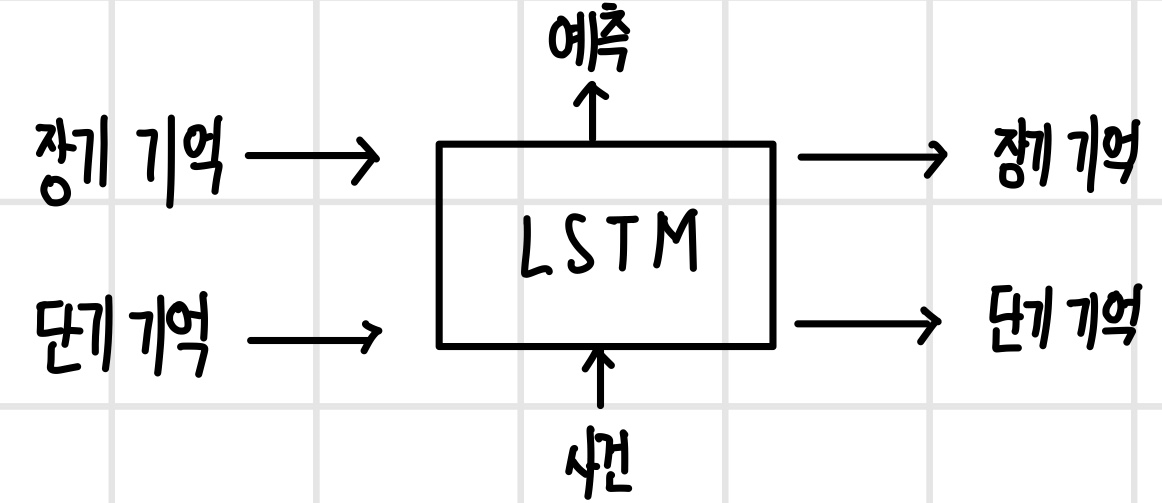
- 셀은 이전 셀에서 장기 기억과 단기 기억을 전달받는다.
- 새로운 사건이 발생 시 장기 기억과 단기 기억을 활용해서 예측과 동시에 장기 기억과 단기 기억을 갱신하여 다음 셀에 전달한다.
- 이전 셀에서 전달된 장기 기억 중에서 더 기억할 필요가 없는 기억은 지워버린다.
- 단기 기억에는 최근 사건에 대한 콘텍스트가 있어 새로운 사건이 들어올 때 함께 기억을 새롭게 형성하는 데 관여한다.
- 새롭게 형성된 기억의 일부는 장기 기억으로 전환되고, 이로부터 갱신된 콘텍스트를 갖는 단기 기억을 만들어 현재 단계의 예측에 활용한다.
기억을 선택하는 게이트 구조
LSTM에는 기억을 형성하는 데 관여하는 네 종류의 게이트가 있으며, `게이트`는 기억을 지속할지 잊을지 선택하는 역할을 한다. 현재 콘텍스트에 부합하고 자주 사용되는 기억은 지속하지만 그렇지 않은 기억은 잊도록 한다. LSTM 셀 안에는 `망각 게이트(forget gate)`, `입력 게이트(input gate)`, `기억 게이트(remember gate)`, `출력 게이트(output gate)`가 있다. 각 게이트의 역할은 다음과 같다.
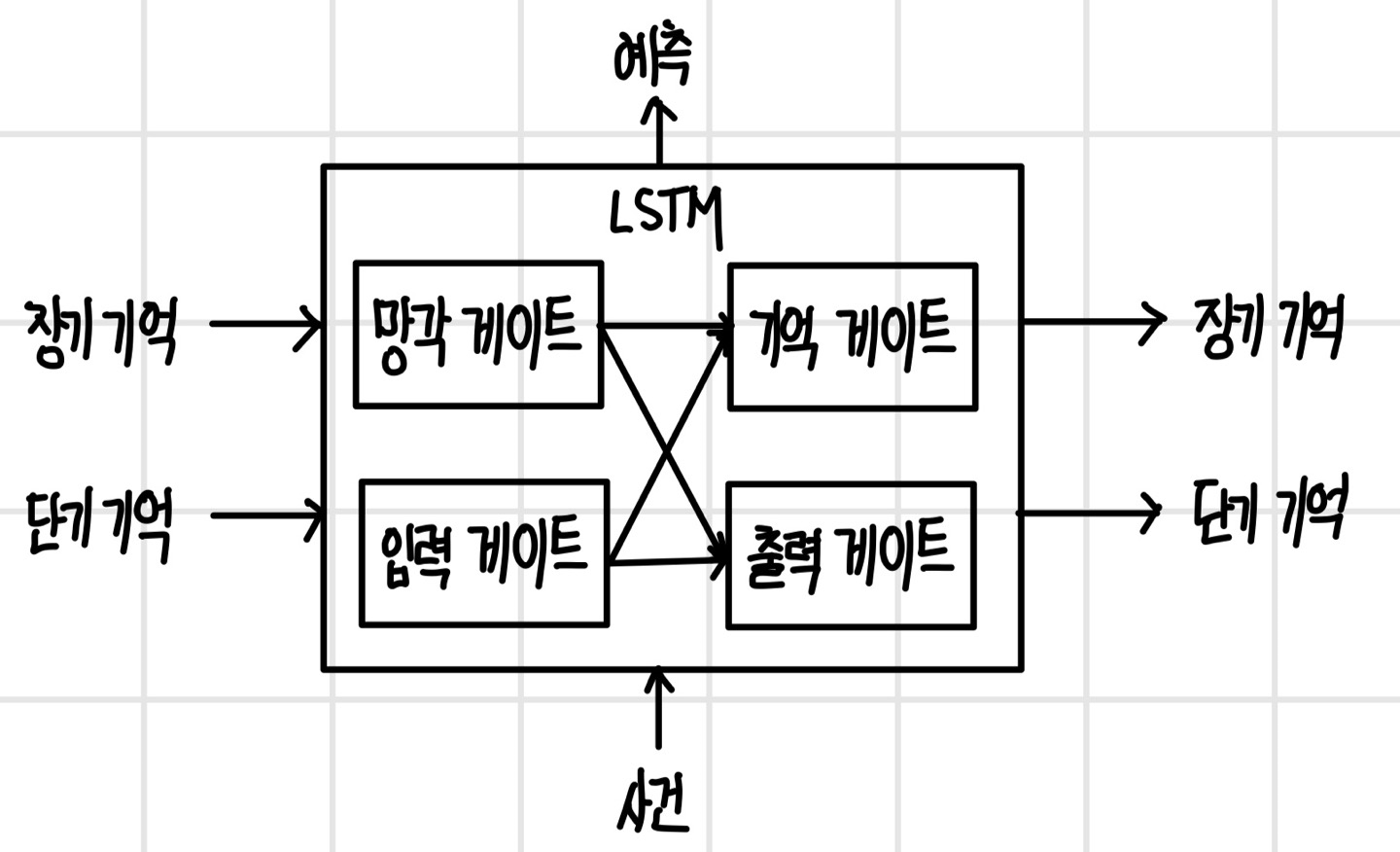
- 망각 게이트 : 장기 기억을 지속할지 잊을지 판단한다. 잊어도 되는 장기 기억은 망각 게이트를 통과하지 못한다.
- 입력 게이트 : 새로운 사건으로 형성된 기억 중 장기 기억으로 전환해야 할 기억을 선택한다.
- 기억 게이트 : 장기 기억을 새롭게 갱신하기 위해 망각 게이트를 통과한 장기 기억에 입력 게이트를 통과한 새로운 기억을 더한다.
- 출력 게이트 : 갱신된 장기 기억에서 갱신된 단기 기억에 필요한 기억을 선택한다.
기억의 흐름과 입력, 출력, 망각 게이트의 역할
LSTM은 게이트 구조를 통해 새롭게 형성된 기억을 지속하거나 지워버린다. 시간의 흐름에 따라 이 과정이 어떻게 진행되는지 다음 그림을 통해 확인이 가능하다. 다음 그림은 첫 번째 사건이 단계 6까지 전달되면서 단계 4와 6의 예측에 활용되는 모습을 나타냈다.
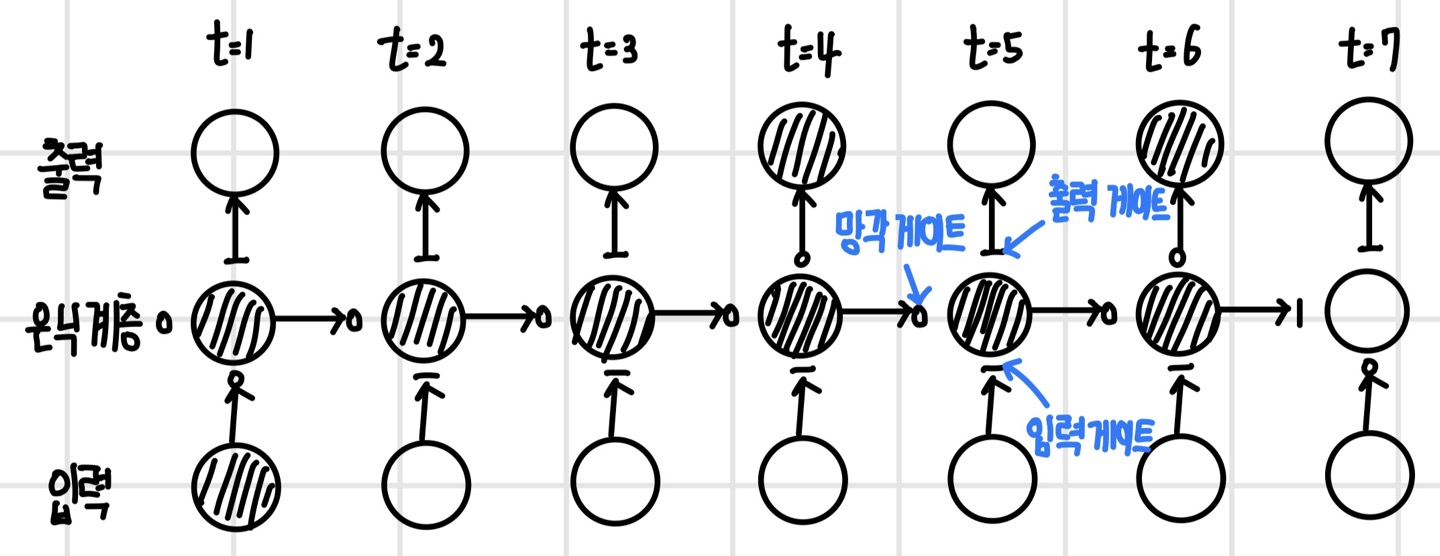
- 첫 번째 사건은 `입력 게이트`를 통해 장기 기억에 반영되어 셀 상태를 거쳐서 6단계까지 전달된다.
- 장기 기억에 있던 첫 번째 사건이 출력 게이트를 통해 단기 기억으로 선택되어 단계 4와 6에서 새로운 사건과 연합하여 단기 기억인 은닉 상태에 반영된다.
- 단기 기억에 반영되면 예측에 바로 활용되며 그다음 단계인 5와 6에 전달된다.
- 일곱 번째 단계에서는 첫 번째 사건의 기억이 더 필요 없다고 판단하고 `망각 게이트`를 통해 장기 기억에서 지워버린다.
LSTM 셀 구조
LSTM의 셀 구조를 도형으로 그리면 다음과 같다.
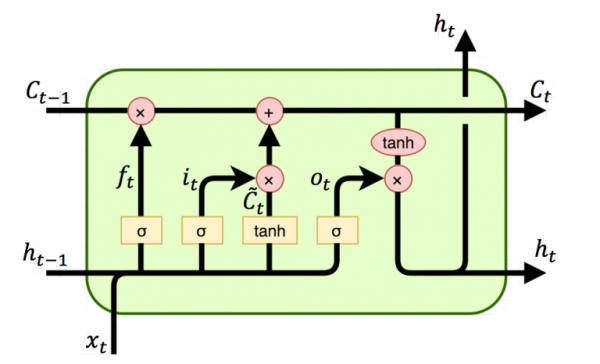
기억을 선택하는 역할을 하는 입력, 망각, 출력 게이트의 값은 단기 기억 h_t-1과 새로운 사건 x_t에 달라진다. 즉, 어떤 기억이 중요한지 선택하는 기준은 순차적으로 발생한 사건의 문맥에 달렸다는 의미이다. 단기 기억 h_t-1과 새로운 사건 x_t는 모든 게이트에 입력으로 들어가며 각기 다른 가중치를 이용해서 가중합산된 후 시그모이드를 통해 값의 범위가 [0,1]로 조정된다. 새로운 기억 또한 단기 기억과 새로운 사건으로 구성되며 값을 [-1,1]로 제한하기 위해 하이퍼볼릭 탄젠트 tanh를 사용한다. 이를 행렬 연산으로 표현하면 다음과 같다.

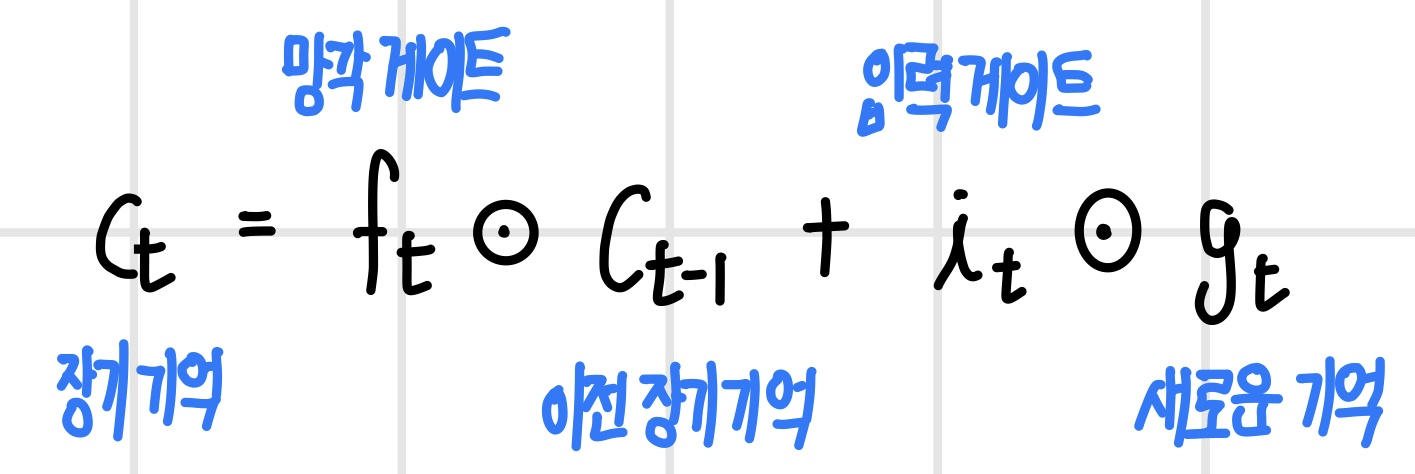
장기 기억에 해당하는 `cell state` C_t는 다음과 같은 식으로 장기 기억과 새로운 기억 중 일부를 선택해서 생성된다. 여기서 C_t는 선형 결합으로 정의되어 계산 과정에 W가 없는 매우 단순한 경로를 구축한다.
단기 기억인 `hidden state` h_t는 새롭게 갱신된 장기 기억 C_t의 일부 기억을 선택해서 생성된다. 먼저 cell state에 하이퍼볼릭 탄젠트를 실행해서 값의 범위를 [-1,1]로 변환하고, 변환된 값에 출력 게이트와의 요소별 곱 연산을 하여 필요한 기억을 선택한다. 이는 출력 계층에 전달되어 현재 단계의 예측에 사용된다.

그레이디언트 소실이 생기지 않는 이유
cell state를 연결하는 경로에서 그레이디언트 소실이 발생하지 않는 이유는 RNN에서 문제가 되었던 W의 반복적인 곱 연산이 사라졌기 때문이다. C_t의 C_t-1에 대한 지역 그레이디언트는 다음과 같으며, 연쇄 법칙으로 역방향의 미분을 계산해 보면 망각 게이트의 곱으로 바뀐다. 이 값은 셀마다 다르기 때문에 그레이디언트 소실을 발생시킬 가능성이 적다.
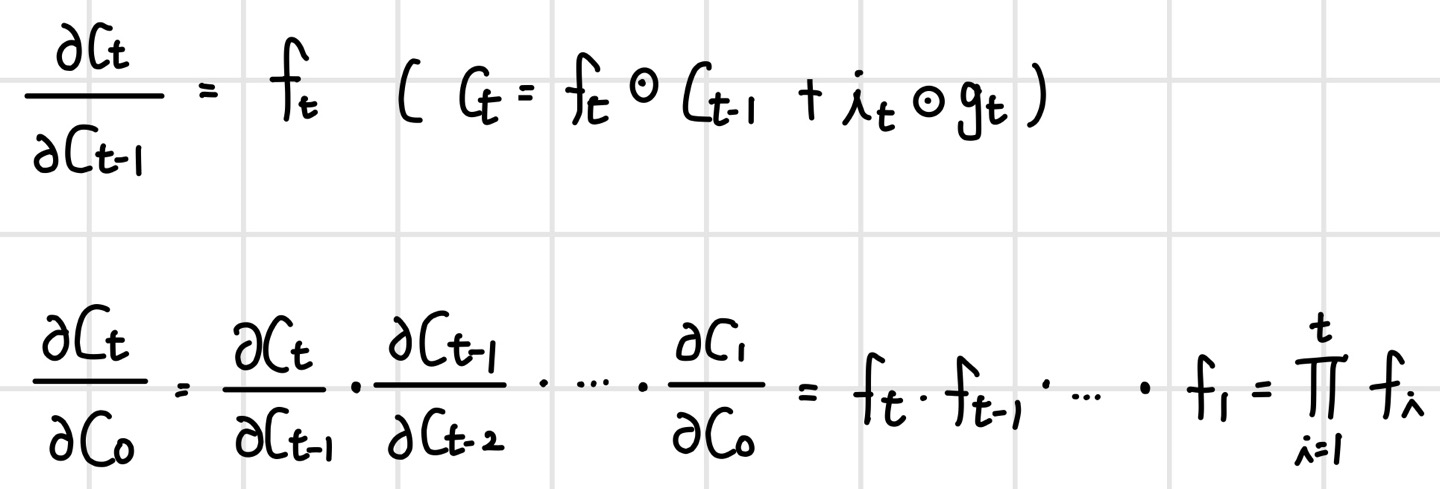
GRU(Gated Recurrent Unit)
`GRU(Gated Recurrent Unit)`는 LSTM의 장점을 유지하면서 게이트 구조를 단순하게 만든 순환 신경망이다. GRU는 cell state를 없애고 다시 hidden state가 장기 기억과 단기 기억을 모두 기억하도록 했다. 다음 그림을 보면 h_t-1과 h_t 사이에 경로가 두 갈래로 분기되다가 다시 합쳐지는 구조로 이루어진다. 위쪽 경로는 W의 연산이 없는 장기 기억을 전달하는 지름길이고 아래쪽 경로는 W의 연산이 있는 단기 기억을 전달하는 경로이다.
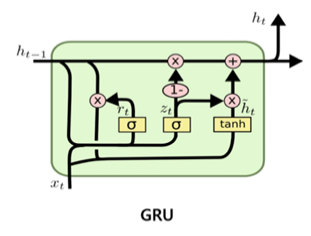
게이트 또한 두 가지로 간소화되었다. 먼저 `리셋 게이트(reset gate)` r_t는 새로운 사건이 발생했을 때 기억을 새롭게 형성하기 위해 장기 기억과 단기 기억에서 필요한 부분을 선택한다. `업데이트 게이트(update gate)` z_t는 기억을 갱신하기 위해 기존 기억과 새롭게 형성된 기억의 가중 평균을 계산하는 가중치 역할을 한다. 각 게이트와 새롭게 형성된 기억의 계산은 다음과 같다. 새로운 기억의 형성 과정을 보면, 리세 게이트는 이전 상태에서 필요한 부분을 선택하는 것을 알 수 있다.
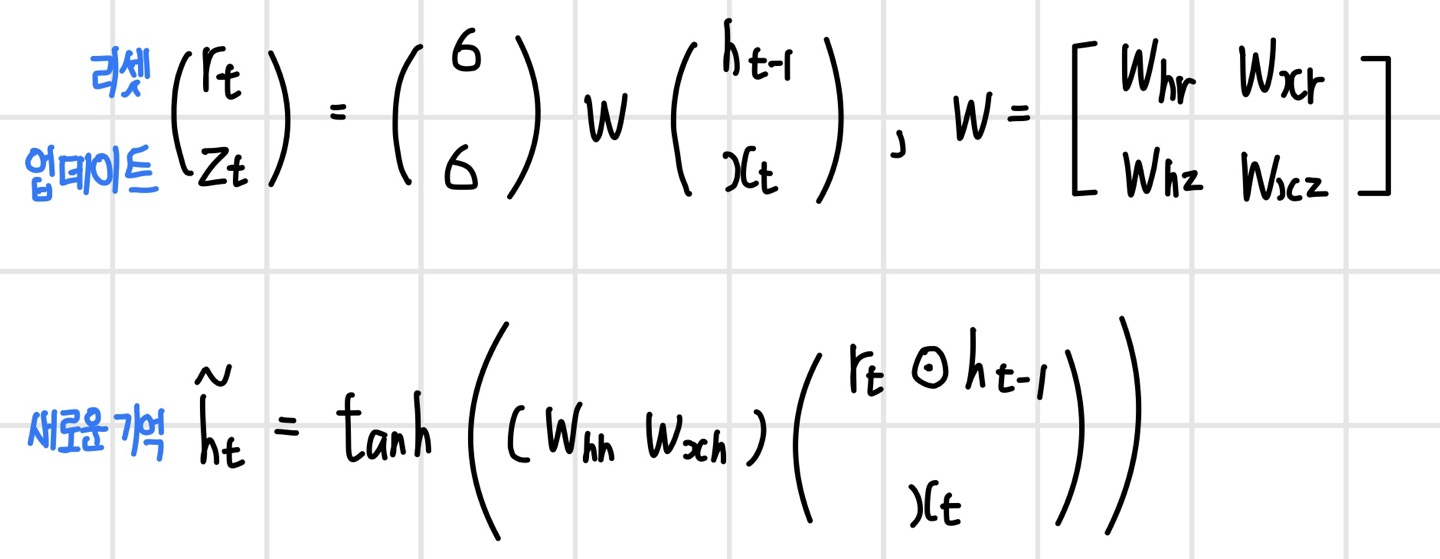
갱신된 기억인 hidden state는 이전 상태와 새로운 사건으로 형성된 기억의 가중 평균으로 계산된다. 업데이트 게이트는 이전 상태와 새로운 상태의 반영 비율을 결정하는 가중치로 활용된다. 이러한 GRU는 LSTM에 비해 셀 구조가 단순해지고 연산량도 줄었지만 성능은 비슷하다.

순환 신경망 개선
LSTM과 GRU과 같은 새로운 순환 신경망의 등장으로 장기 의존성 문제와 그레이디언트 폭발 문제가 조금 완화되었지만, 여전히 구조적으로 이 문제를 완전히 해결하긴 어렵다. 여전히 많은 문제에서 더욱 긴 콘텍스트를 다뤄야 하기 때문에 이를 다루기 위한 다양한 방법들이 나오고 있다. `어텐션(attention)`은 모든 기억을 동등하게 기억하지 않고 연관성 있는 기억에 집중해서 기억하도록 구조화하는 방법이다. 초기 어텐션 모델은 순환 구조에 어텐션을 결합한 형태였지만, 최근 모델은 순환 구조를 배제하고 어텐션 계층과 완전 연결 계층만을 사용한다. `시간 팽창 컨벌루션(temporal dilated convolution)`은 오래전 기억이 빠르게 전달되도록 모델을 계층화하는 방법으로, 순환 구조를 전혀 사용하지 않는다. 어텐션은 다양한 모델과 쉽게 결합되어 시간 팽창 컨벌루션과 같이 사용할 수도 있다.
어텐션(attention)
`어텐션(attention)`이란 뇌가 가장 중요하고 연관성 있는 정보에 집중하는 것을 말한다. 언어 모델에 어텐션을 적용한다면 문장의 특정 단어를 볼 때 문장 내의 다른 단어와의 연관성을 `어텐션값(attention value)`로 사용한다. 어텐션을 계산하려면 `키(key)`와 `값(value)`으로 이루어진 (k, v) 목록과 `쿼리(query)` q가 정의되어야 한다. 쿼리 q를 기준으로 각 키 k와의 연관 정도를 계산하며, 그에 비례해서 키에 대응되는 값 v를 어텐션 값으로 사용한다. 따라서 키 k는 쿼리 q와의 연관 정도를 계산할 대상이고, 값 v는 연관 정도에 따라 사용할 데이터이다.
다음 그림은 어텐션을 계산하는 순서이다. 먼저 q와 (k,v) 목록의 각 키 k와 `어텐션 점수(attention score)`를 계산한다. 어텐션 점수는 쿼리 q와 키 k의 연관 정도를 의미하며 다양한 함수로 표현될 수 있다. 계산된 어텐션 점수와 값 v를 곱해서 모두 합산하거나 가장 큰 어텐션 점수와 대응되는 v를 곱해서 최종 어텐션으로 사용한다. 어텐션 점수는 쿼리와 키 사이에 연관성 또는 유사도를 나타내기 때문에 보통 `내적(dot-product)` 또는 내적을 변형한 방법으로 계산하며, 종종 어텐션 점수에 `소프트맥스` 함수를 적용해 확률로 변환하기도 한다.
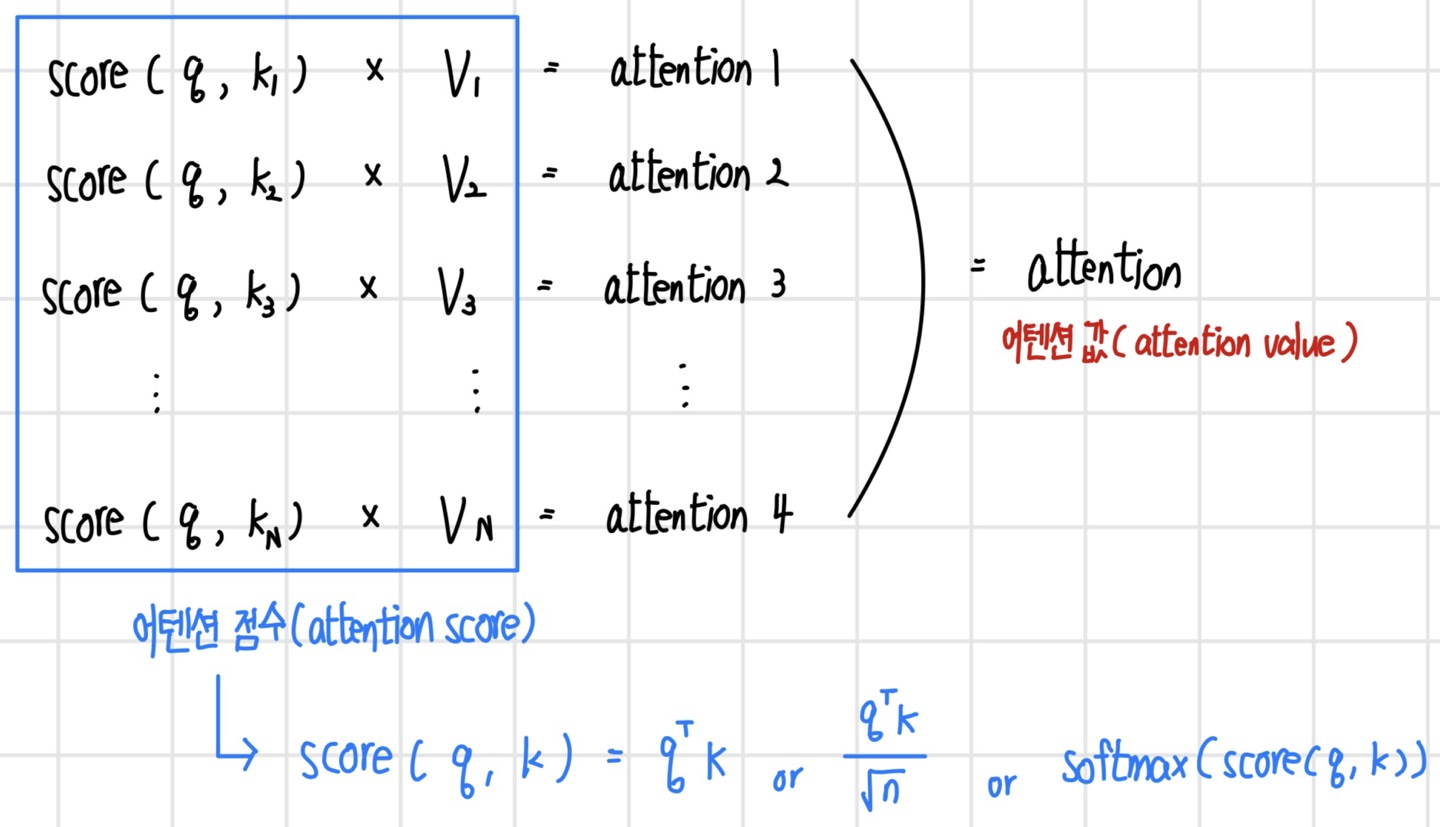
`셀프 어텐션(self attention)`은 자기 자신을 구성하는 부분끼리 연관성을 찾고자 할 때 사용하는 어텐션 방법이다. 예를 들어 문장 내에 현재 단어와 연관성이 있는 단어를 찾거나, 이미지에서 의미적으로 서로 연관성 있는 부분을 찾을 때 사용한다. 또한 어텐션은 계산하는 방식에 따라 `하드 어텐션(hard attention)`과 `소프트 어텐션(soft attention)`을 구분한다. 하드 어텐션은 가장 집중하는 선택하는 방식으로 어텐션 점수 중 최댓값으로 계산한다. 소프트 어텐션은 어텐션 점수를 자중치로 사용해서 전체 정보를 가중 합산하는 어텐션 계산 방법이다.
이 포스팅은 'Do it! 딥러닝 교과서' 교재를 공부하고 작성한 글입니다.