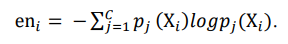목차
논문 정보
0.Abstract
- CNN-based deep learning models을 통해 정확하게 웨이퍼 빈 맵(WBM)의 결함 패턴을 분류하기 위해선 정확한 결함 패턴의 label이 반드시 있어야 한다.
- 하지만 현실에선 엔지니어가 모든 데이터에 label을 다는 것은 많은 시간과 노력이 필요하다.
- 현재 CNN-based 연구들은 실제 상황에서 빈번하게 발생하는 새로운 결함 패턴을 찾지 못하는 한계점을 가지고 있다.
- 본 논문에서는
Active Learning에 기반한 새로운 결함 패턴 탐지 방법을 제안한다.- 또한 모델 훈련 단계에서 사용되지 않은 새로운 결함 패턴을 빠르게 탐지하는 새로운 프레임워크 또한 제안한다.
- 본 방식의 유용성과 적용성은 공공적으로 이용이 가능한 WBM 데이터인 WM-811K 데이터를 통해 증명된다.
1. 서론
- 반도체 제조 공정이 완료되면 불량을 확인하기 위해 완성된 웨이퍼 위의 반도체칩이 정상적으로 작동되는지 확인하는
EDS(Electrical Die Sorting)검사를 진행한다.- 이 EDS 검사의 결과 데이터로
웨이퍼 빈 맵(wafer bin map, WBM)이 생성된다.
- 이 EDS 검사의 결과 데이터로
- WBM은 불량의 원인에 따라 특정한 불량 패턴을 가진다.
- 동일한 형태의 불량 패턴을 갖는 웨이퍼는 그 불량의 유발 원인도 동일한 것임을 추측할 수 있다.
- 특정한 패턴이 일정 기간 내에 다수 발생한다면 엔지니어는 이를 통해 불량의 원인을 파악하고 조치할 수 있다.
- 머신러닝 모델을 통해 WBM 이미지로부터 특징을 추출하고 불량 패턴을 분류하는 데 실제 산업 현장에선 3가지의 문제점이 있다.
- 매일 수만 매 이상 검사 데이터가 만들어지는데, 이는 레이블이 없는(unlabeled)데이터로 이에 대한 분류 비용을 최소화할 수 있어야 한다.
- 일반적으론 기존에 경험한 불량 패턴이 반복적으로 발생하지만, 간헐적으로 신규 패턴이 발생하며 이로 인해 품질 사고로 이어질 확률이 크다.
- 신규 패턴 또한 하나의 '신규' 클래스로 분류하는 것이 아닌 신규 패턴 종류별로 분류 성능을 획득할 수 있어야 한다.
- 이러한 상황에 준지도학습의 일종인 액티브 러닝(active learning)이 효과적으로 사용될 수 있다.
![]()
Active Learning process - 먼저 소량의 레이블이 있는 데이터를 가지고 모델을 구축한다.
- 이렇게 구축된 모델은 다시 unlabeled 데이터의 레이블을 예측하면서, 앞으로 성능 향상에 도움을 줄 수 있는 샘플을 골라내 엔지니어에게 제공한다.
- 어떤 샘플이 성능에 도움이 될지 계산하여 샘플링하는 단계를
샘플링 전략(sampling strategy)라고 표현한다. - 엔지니어는 이 샘플을 레이블링하여 기존 학습 모수에 업데이트한 뒤 모델을 재학습 시키면, 모델은 양질의 학습 데이터의 증가로 인해 성능을 높일 수 있다.
- 어떤 샘플이 성능에 도움이 될지 계산하여 샘플링하는 단계를
- 본 논문의 주요 기여점은 다음과 같다.
- 웨이퍼 빈 맵 분류 문제에 액티브 러닝을 적용하여 신규 패턴을 가진 웨이퍼를 조기에 검출 할 수있는 방법론을 제안한다.
- 다양한 샘플링 방식을 적용하여 신규 패턴 검출에 알맞는 방법론을 비교하였으며, 단기간에 신규 패턴에 대한 정확도를 확보하였다.
3. 제안 방법론
3-1. Data Preprocessing
- 기존 811,467매의 웨이퍼 빈 맵 오픈 데이터에서 레이블이 있는 172,950매를 데이터로 사용
- 각 웨이퍼의 크기가 64x64로 통일되도록 스케일링하고, 0 : Wafer가 없는 영역 / 1 : 양호 Chip / 2: 불량 Chip으로 나눠지도록 [64x64x3] 차원의 이미지 형태로 변경
- 전체의 20%는 테스트셋으로 분리하고, 나머지 80%는 전부 표기된 레이블을 가려 unlabeled 데이터로 만들어 실제 제조 현장과 동일한 상황을 가정
- 모델을 구축하기 위해 전체의 1% 수준(약 1,714매)만을 레이블링하여 사용
- Active Learning에서의 사람이 레이블링 하는 과정은 가려진 레이블을 다시 가져오는 것으로 대체
- 신규 패턴 가정을 위해 데이터의 개수가 가장 적은
Random,Donut,Near-Full세 가지 패턴을 최초 모델 구축을 위한 훈련 데이터에서 제외
3-2. Active Learning Structure Overview
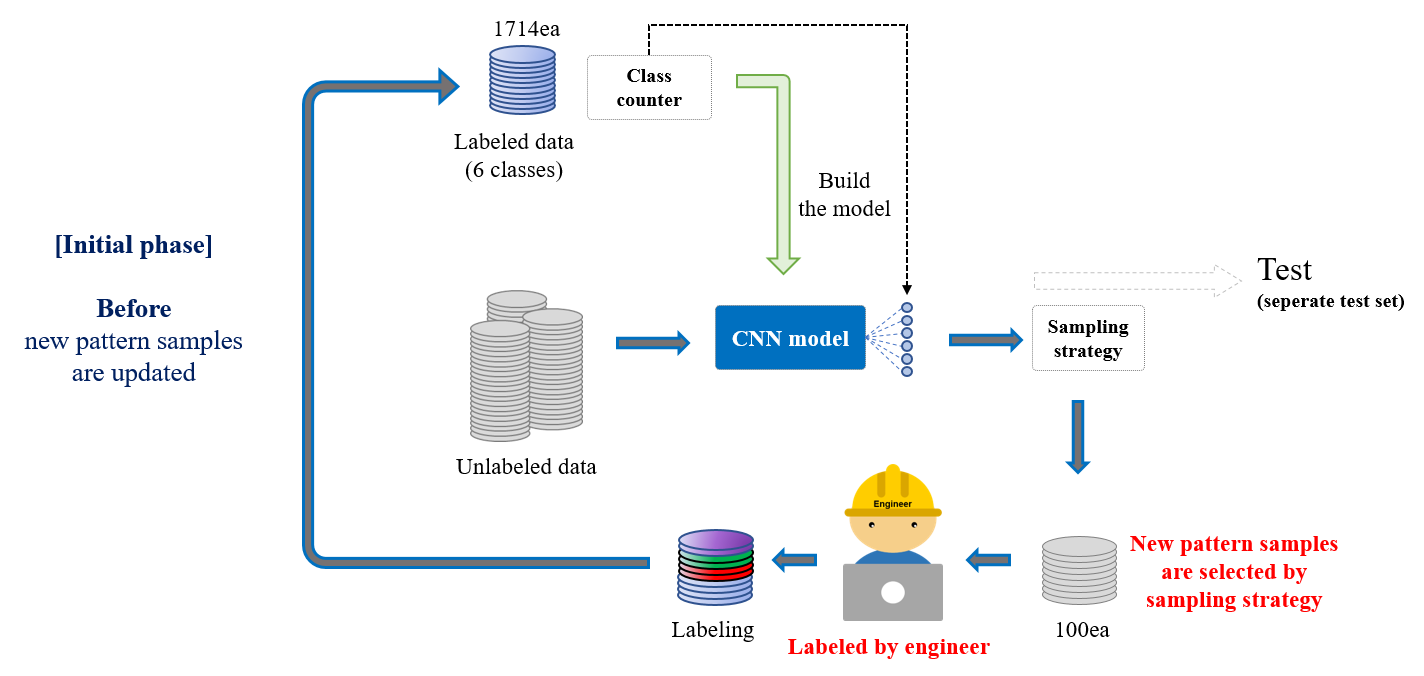
- 기존 Active Learning과 다르게 제안하는 모델의 구조는 신규 패턴을 검출하여 이를 모델이 학습할 수 있도록 만드는 것이 주 목적
- 먼저 레이블링된 초기 훈련 데이터(1.714매)를 통해 모델이 구축되고 나면, unlabeled 데이터를 모델에 입력하여 계산된 출력값을 샘플링 전략에 사용
- 샘플링 전략은 unlabeled 샘플 중 모델이 분류하기 어렵거나, 기존의 분류에 적합하지 않은 샘플로 k개를 뽑도록 계산
- 본 연구에선 100개씩(k=100) 샘플링되어 엔지니어에게 제공
- '모델 학습 -> 샘플링 전략 -> 엔지니어 레이블링 -> 훈련 데이터 업데이트'의 단계가 1 phase
- 액티브 러닝은 phase를 반복할 때마다 훈련 데이터의 개수가 초기 1714매 + (100 x n phase)만큼 늘어나면서 성능 향상
- 기존 연구와 달리 본 연구는 알고 있는 패턴에 대한 분류 성능만으로 샘플링 전략에 의해 현재 분류와는 다른 특징 벡터를 골라낼 수 있어 신규 패턴이 감지될 수 있을 것이라고 가정
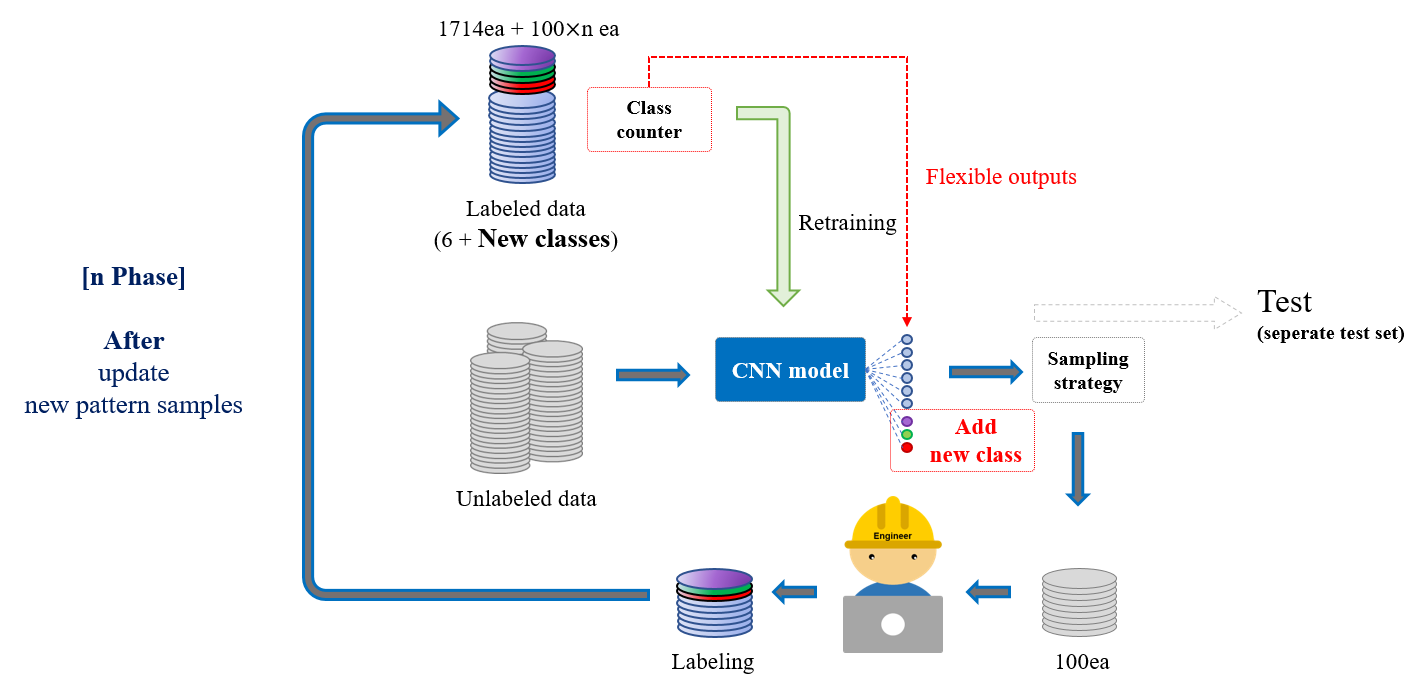
- Active Learning의 샘플링 전략이 엔지니어에게 신규 패턴을 가진 샘플을 제공하며, 엔지니어는 이를 신규 클래스로 분류하여 훈련 데이터를 업데이트하면 모델은 신규 패턴에 대한 성능을 확보
- 출력 클래스의 개수는 기존 6개에서 6+a로 변하게 조정
- 모델의 출력 클래스의 개수가 변하여도 늘어난 클래스에 맞춰 추가 학습만 진행되게끔 가중치(weight) 유지
- 최종적으로 모델은 신규 패턴을 포함한 9개 전체 클래스에 대해 전부 일정 수준 이상의 성능을 확보
3-3. Convolution Neural Network Classification Model
- 대량의 unlabeled 데이터에 대해 반복적인 계산을 수행해야 하므로 모델의 복잡도를 줄여 효율성을 극대화 -> 비교적 가벼운 모델
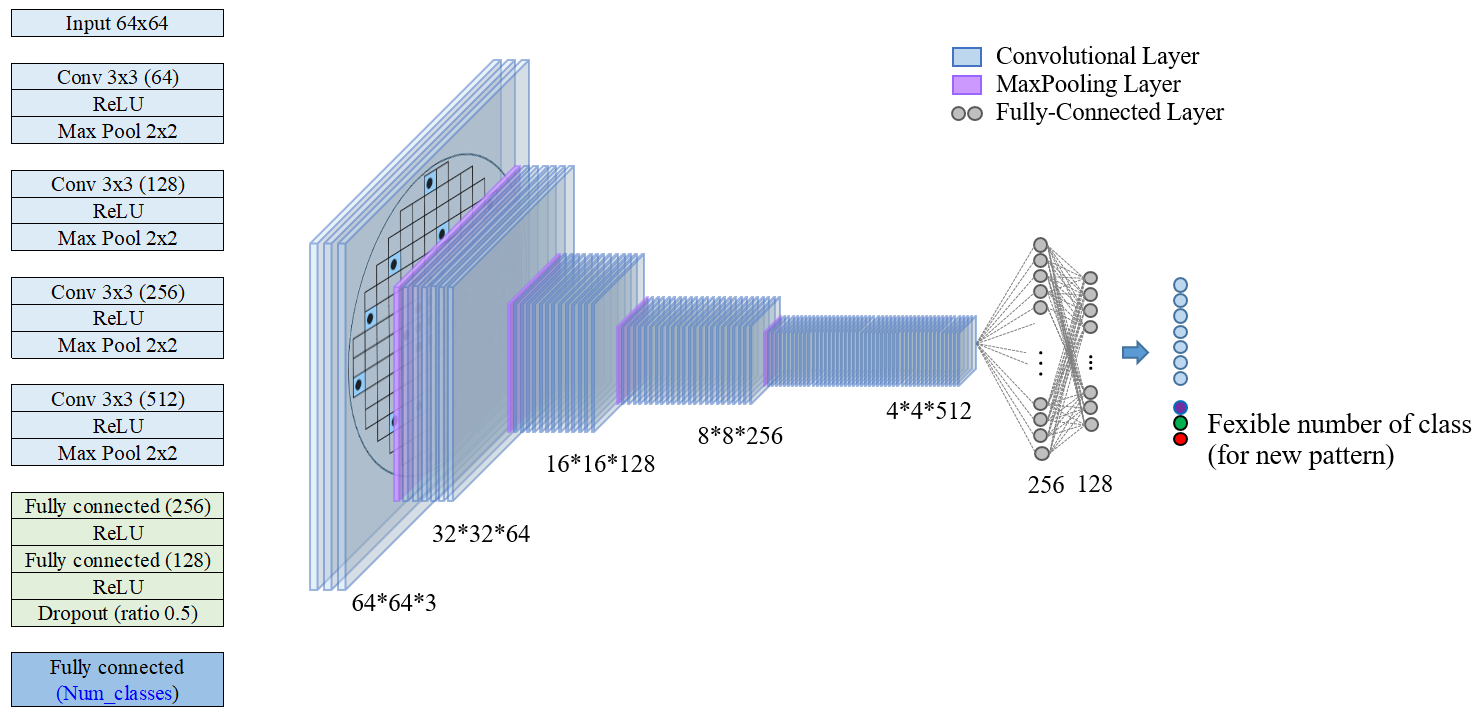
- 4개의 Convolutional layer
- kernel size = (3,3)
- channel : 64, 128, 256, 512
- 활성화 함수 : ReLU
- 2x2 max pooling을 통해 크기를 반으로 줄이며 진행
- 마지막에 fully-connected layer 2개를 사용하여 256, 128 차원으로 특징 벡터를 추출
- 각 클래스별 확률을 구하고 소프트맥스를 사용해 분류
3-4. Sampling Strategy
- 확률적 접근, 베이지안 접근, 거리 접근
- 이들은 모두 샘플에 대한 모델의 예측이 불확실할수록 판단하기 어려운 샘플이며 해당 샘플이 모델 성능에 더 도움이 된다 가정
- 따라서 이러한
불확실성을 측정하는 방법을 설명
확률적 접근
- 샘플이 어떠한 분류에도 속할 확률이 높지 않은 경우 현재의 모델이 판단하기 어려운 샘플
- 최소 신뢰(least confidence) 샘플링
신뢰값(confidence): 샘플이 갖는 확률 중에 가장 큰 값- 신뢰값이 작을수록 불확실성이 높다고 판단
- 어떤 분류로도 속하기 어려운 샘플일수록 낮은 신뢰값을 가지며, 이를 샘플로 선정하면 신규 패턴을 선택할 가능성 증가
![]()
- 최소 확률차(least margin) 샘플링
- 샘플이 갖는 확률 중에 가장 큰 값과 두 번째 큰 값의 차이가 작을수록 선택
- 최소 신뢰 샘플링을 보완
![]()
- 엔트로피(entropy) 샘플링
- 분류 확률값을 통해 계산한 엔트로피로 불확실성을 정의
- 엔트로피가 가장 높은 샘플이 불확실성이 높다고 판단하여 선택
![]()
베이지안 샘플링
- 베이지안 신경망 모델을 사용하여 불확실성을 계산
- 불일치를 통한 베이지안 동적 학습(Bayesian active learning by disagreement, BALD)을 사용
- 베이지안 신경망에서의 불확실성 값이 큰 샘플일수록 모델이 판단하기 어려워 훈련 데이터로 학습 시 모델 학습에 도움이 되는 샘플로 판단
- 불확실성은
드롭아웃(Dropout)을 반복적으로 수행했을때 변화하는 출력값의 분포를 통해 추정- 모델로 한 샘플에 대해 N회 반복 예측할 때마다 드롭아웃에 의해 배제되는 노드들의 바뀌면서 서로 다른 N개의 예측 확률 계산
![]()
- 모델로 한 샘플에 대해 N회 반복 예측할 때마다 드롭아웃에 의해 배제되는 노드들의 바뀌면서 서로 다른 N개의 예측 확률 계산
거리 접근
- 샘플들의 중심에서 가장 멀리 떨어진 샘플이 불확실성이 높다고 보는 방식 ->
K-means clustering사용 - 모델로부터 출력된 샘플별 특성 벡터으로부터 군집화르르 통해 중앙값을 확인하고 이 중앙값에서 가장 멀리 떨어진 샘플 선택
![]()
4. 실험 결과
4.1 평가지표 & 4.2 실험 조건
- 평가 지표
F1-score: 다중 클래스 분류에서 널리 사용되는 지표로, 클래스 불균형이 심한 상황에서 유용하게 사용
- 실험 조건
- 손실 함수 :
cross entropy - 모델의 최적화 알고리즘 :
RMSProp - 하이퍼 파라미터 :
learning_rate: 0.0005,momentum: 0.3,L2 정규화 상수: 0.0001 - 최초 훈련 데이터는 1,714매(6개 클래스)로 시작하여 매 phase마다 100매씩 추가로 50phase 진행
- 각 phase별 300 epoch
- validation loss가 25번 개선된 변화가 없으면
조기 종료(early stopping)
- 모델 성능 평가는 모든 클래스가 존재하는 테스트 데이터(전체의 20%, 9개 클래스)
- 초기에 모델이 신규 패턴을 감지하지 못하는 경우 예측 활률을 0으로 처리
- 모든 실험은 샘플링 전략마다 난수 설정을 바꿔가며 10회 반복하여 평균값 사용
- 손실 함수 :
4.3 실험 결과
4.3.1 분류 성능 결과
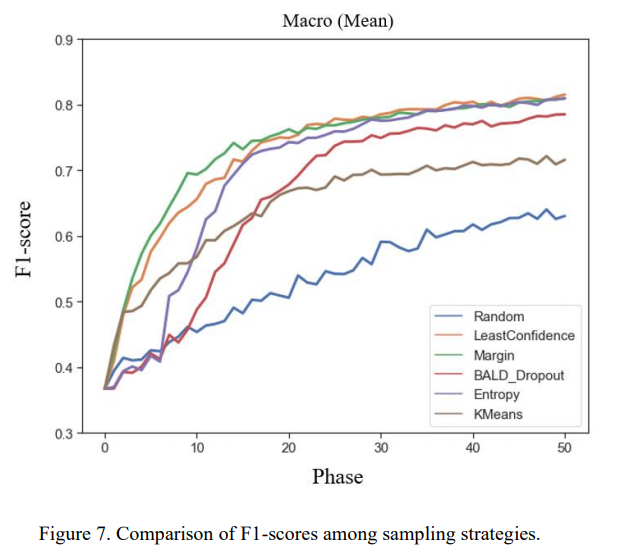
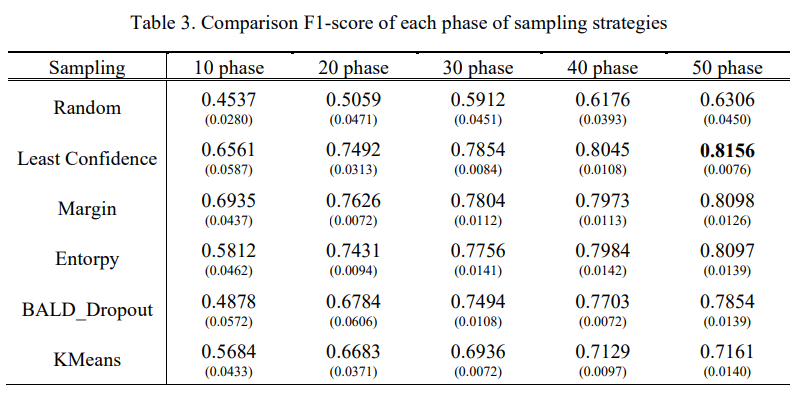
- 최초 구축된 모델은 분류 성능이 부족하지만, phase를 반복하며 훈련 데이터를 쌓을수록 성능 향상
- 무작위 샘플링 전략은 훈련데이터가 늘어도 성능 향상 저조
- 다른 샘플링 전략은 무작위 샘플링 대비 성능이 빠르게 향상되어 최종적으로도 더 높은 분류 성능 기록
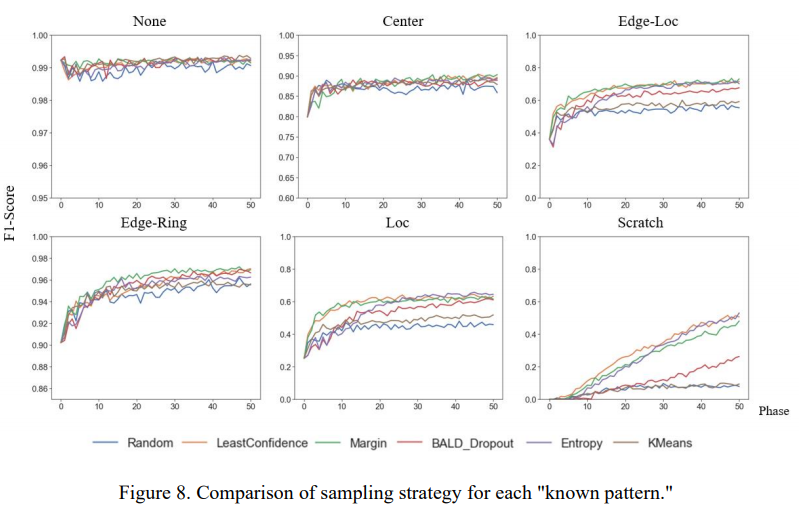
- 모수가 많은
None,Center패턴에서는 최초부터 높은 분류 성능을 보이고 샘플링 전략 간 유의차 미약 Edge-Loc,Edge-Ring,Loc과 같은 패턴에서는 샘플링 전략을 통해 더 높은 성능 확보Scratch와 같이 수가 적은 클래스 패턴의 경우 성능의 유의차가 더욱 큼
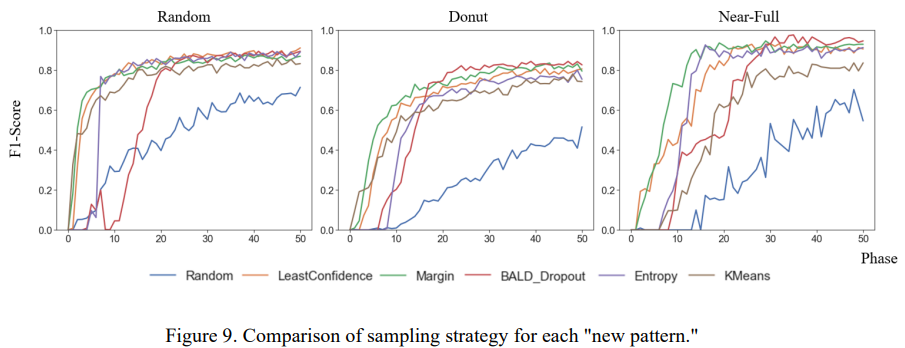
- 신규 패턴의 경우 액티브 러닝에 따라 업데이트된 샘플 양에 의존하기 때문에 성능차가 더욱 큼
- 본 연구에서 제안하는 방법론은 20 phase 이내 구간에서 빠른 속도로 신규 패턴에 대한 성능 향상
- 샘플링 전략에 의해 감지된 신규 패턴 샘플이 훈련 데이터로 다수 업데이트되었기 때문
- 샘플링 전략이 신규 패턴 검출에 효과적으로 사용 가능
4.3.2 Train Data(Labeled) Count
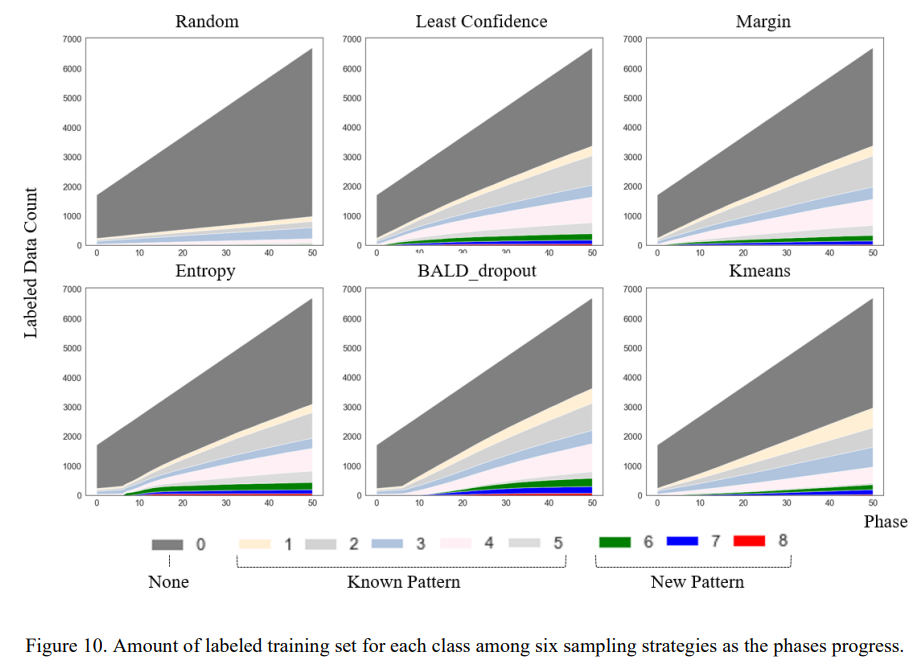
- 6개의 각 샘플링 전략별로 훈련 데이터를 업데이트함에 따라 증가하는 각 클래스별 훈련 모수 표시
- 최초 모델 시 1,714매로 시작하여 phase마다 100매씩 늘려갈 때, 어떤 클래스의 샘플로 업데이트 했는가에 따라 비율이 달라짐
- 무작위 샘플링의 경우 처음 none 패턴이 모수의 대부분을 차지하며, phase가 진행되어도 최초의 클래스 비율이 유지
- none 패턴이 훈련 데이터의 대부분을 차지하고 극소수인 신규 패턴에 대한 업데이트는 거의 x
- 제안하는 샘플링 방법론에서는 none이 아닌 클래스의 비율이 확연하게 증가
- 극소수의 신규 패턴도 훈련 데이터로 다수 업데이트되는 것을 확인 가능
- none 패턴이 훈련 데이터의 대부분을 차지하고 극소수인 신규 패턴에 대한 업데이트는 거의 x
5. 결론
- 공정 내에서 발생하는 신규 패턴에 대해 그것을 인지하지 못하면 큰 품질 사고로 이어질 가능성이 높으므로 고려 필요
- 문제가 된 웨이퍼가 어떤 이력을 가졌는지 확인하기 위해서 이러한 샘플 데이터를 확보하는 것 중요
- Active Learning을 통해 신규 패턴 샘플을 확보하면서도 실험 결과를 통해 충분히 높은 수준의 정확도 획득 가능 확인
논문 정보
0.Abstract
- CNN-based deep learning models을 통해 정확하게 웨이퍼 빈 맵(WBM)의 결함 패턴을 분류하기 위해선 정확한 결함 패턴의 label이 반드시 있어야 한다.
- 하지만 현실에선 엔지니어가 모든 데이터에 label을 다는 것은 많은 시간과 노력이 필요하다.
- 현재 CNN-based 연구들은 실제 상황에서 빈번하게 발생하는 새로운 결함 패턴을 찾지 못하는 한계점을 가지고 있다.
- 본 논문에서는
Active Learning에 기반한 새로운 결함 패턴 탐지 방법을 제안한다.- 또한 모델 훈련 단계에서 사용되지 않은 새로운 결함 패턴을 빠르게 탐지하는 새로운 프레임워크 또한 제안한다.
- 본 방식의 유용성과 적용성은 공공적으로 이용이 가능한 WBM 데이터인 WM-811K 데이터를 통해 증명된다.
1. 서론
- 반도체 제조 공정이 완료되면 불량을 확인하기 위해 완성된 웨이퍼 위의 반도체칩이 정상적으로 작동되는지 확인하는
EDS(Electrical Die Sorting)검사를 진행한다.- 이 EDS 검사의 결과 데이터로
웨이퍼 빈 맵(wafer bin map, WBM)이 생성된다.
- 이 EDS 검사의 결과 데이터로
- WBM은 불량의 원인에 따라 특정한 불량 패턴을 가진다.
- 동일한 형태의 불량 패턴을 갖는 웨이퍼는 그 불량의 유발 원인도 동일한 것임을 추측할 수 있다.
- 특정한 패턴이 일정 기간 내에 다수 발생한다면 엔지니어는 이를 통해 불량의 원인을 파악하고 조치할 수 있다.
- 머신러닝 모델을 통해 WBM 이미지로부터 특징을 추출하고 불량 패턴을 분류하는 데 실제 산업 현장에선 3가지의 문제점이 있다.
- 매일 수만 매 이상 검사 데이터가 만들어지는데, 이는 레이블이 없는(unlabeled)데이터로 이에 대한 분류 비용을 최소화할 수 있어야 한다.
- 일반적으론 기존에 경험한 불량 패턴이 반복적으로 발생하지만, 간헐적으로 신규 패턴이 발생하며 이로 인해 품질 사고로 이어질 확률이 크다.
- 신규 패턴 또한 하나의 '신규' 클래스로 분류하는 것이 아닌 신규 패턴 종류별로 분류 성능을 획득할 수 있어야 한다.
- 이러한 상황에 준지도학습의 일종인 액티브 러닝(active learning)이 효과적으로 사용될 수 있다.
![]()
Active Learning process - 먼저 소량의 레이블이 있는 데이터를 가지고 모델을 구축한다.
- 이렇게 구축된 모델은 다시 unlabeled 데이터의 레이블을 예측하면서, 앞으로 성능 향상에 도움을 줄 수 있는 샘플을 골라내 엔지니어에게 제공한다.
- 어떤 샘플이 성능에 도움이 될지 계산하여 샘플링하는 단계를
샘플링 전략(sampling strategy)라고 표현한다. - 엔지니어는 이 샘플을 레이블링하여 기존 학습 모수에 업데이트한 뒤 모델을 재학습 시키면, 모델은 양질의 학습 데이터의 증가로 인해 성능을 높일 수 있다.
- 어떤 샘플이 성능에 도움이 될지 계산하여 샘플링하는 단계를
- 본 논문의 주요 기여점은 다음과 같다.
- 웨이퍼 빈 맵 분류 문제에 액티브 러닝을 적용하여 신규 패턴을 가진 웨이퍼를 조기에 검출 할 수있는 방법론을 제안한다.
- 다양한 샘플링 방식을 적용하여 신규 패턴 검출에 알맞는 방법론을 비교하였으며, 단기간에 신규 패턴에 대한 정확도를 확보하였다.
3. 제안 방법론
3-1. Data Preprocessing
- 기존 811,467매의 웨이퍼 빈 맵 오픈 데이터에서 레이블이 있는 172,950매를 데이터로 사용
- 각 웨이퍼의 크기가 64x64로 통일되도록 스케일링하고, 0 : Wafer가 없는 영역 / 1 : 양호 Chip / 2: 불량 Chip으로 나눠지도록 [64x64x3] 차원의 이미지 형태로 변경
- 전체의 20%는 테스트셋으로 분리하고, 나머지 80%는 전부 표기된 레이블을 가려 unlabeled 데이터로 만들어 실제 제조 현장과 동일한 상황을 가정
- 모델을 구축하기 위해 전체의 1% 수준(약 1,714매)만을 레이블링하여 사용
- Active Learning에서의 사람이 레이블링 하는 과정은 가려진 레이블을 다시 가져오는 것으로 대체
- 신규 패턴 가정을 위해 데이터의 개수가 가장 적은
Random,Donut,Near-Full세 가지 패턴을 최초 모델 구축을 위한 훈련 데이터에서 제외
3-2. Active Learning Structure Overview

- 기존 Active Learning과 다르게 제안하는 모델의 구조는 신규 패턴을 검출하여 이를 모델이 학습할 수 있도록 만드는 것이 주 목적
- 먼저 레이블링된 초기 훈련 데이터(1.714매)를 통해 모델이 구축되고 나면, unlabeled 데이터를 모델에 입력하여 계산된 출력값을 샘플링 전략에 사용
- 샘플링 전략은 unlabeled 샘플 중 모델이 분류하기 어렵거나, 기존의 분류에 적합하지 않은 샘플로 k개를 뽑도록 계산
- 본 연구에선 100개씩(k=100) 샘플링되어 엔지니어에게 제공
- '모델 학습 -> 샘플링 전략 -> 엔지니어 레이블링 -> 훈련 데이터 업데이트'의 단계가 1 phase
- 액티브 러닝은 phase를 반복할 때마다 훈련 데이터의 개수가 초기 1714매 + (100 x n phase)만큼 늘어나면서 성능 향상
- 기존 연구와 달리 본 연구는 알고 있는 패턴에 대한 분류 성능만으로 샘플링 전략에 의해 현재 분류와는 다른 특징 벡터를 골라낼 수 있어 신규 패턴이 감지될 수 있을 것이라고 가정

- Active Learning의 샘플링 전략이 엔지니어에게 신규 패턴을 가진 샘플을 제공하며, 엔지니어는 이를 신규 클래스로 분류하여 훈련 데이터를 업데이트하면 모델은 신규 패턴에 대한 성능을 확보
- 출력 클래스의 개수는 기존 6개에서 6+a로 변하게 조정
- 모델의 출력 클래스의 개수가 변하여도 늘어난 클래스에 맞춰 추가 학습만 진행되게끔 가중치(weight) 유지
- 최종적으로 모델은 신규 패턴을 포함한 9개 전체 클래스에 대해 전부 일정 수준 이상의 성능을 확보
3-3. Convolution Neural Network Classification Model
- 대량의 unlabeled 데이터에 대해 반복적인 계산을 수행해야 하므로 모델의 복잡도를 줄여 효율성을 극대화 -> 비교적 가벼운 모델

- 4개의 Convolutional layer
- kernel size = (3,3)
- channel : 64, 128, 256, 512
- 활성화 함수 : ReLU
- 2x2 max pooling을 통해 크기를 반으로 줄이며 진행
- 마지막에 fully-connected layer 2개를 사용하여 256, 128 차원으로 특징 벡터를 추출
- 각 클래스별 확률을 구하고 소프트맥스를 사용해 분류
3-4. Sampling Strategy
- 확률적 접근, 베이지안 접근, 거리 접근
- 이들은 모두 샘플에 대한 모델의 예측이 불확실할수록 판단하기 어려운 샘플이며 해당 샘플이 모델 성능에 더 도움이 된다 가정
- 따라서 이러한
불확실성을 측정하는 방법을 설명
확률적 접근
- 샘플이 어떠한 분류에도 속할 확률이 높지 않은 경우 현재의 모델이 판단하기 어려운 샘플
- 최소 신뢰(least confidence) 샘플링
신뢰값(confidence): 샘플이 갖는 확률 중에 가장 큰 값- 신뢰값이 작을수록 불확실성이 높다고 판단
- 어떤 분류로도 속하기 어려운 샘플일수록 낮은 신뢰값을 가지며, 이를 샘플로 선정하면 신규 패턴을 선택할 가능성 증가
![]()
- 최소 확률차(least margin) 샘플링
- 샘플이 갖는 확률 중에 가장 큰 값과 두 번째 큰 값의 차이가 작을수록 선택
- 최소 신뢰 샘플링을 보완
![]()
- 엔트로피(entropy) 샘플링
- 분류 확률값을 통해 계산한 엔트로피로 불확실성을 정의
- 엔트로피가 가장 높은 샘플이 불확실성이 높다고 판단하여 선택
![]()
베이지안 샘플링
- 베이지안 신경망 모델을 사용하여 불확실성을 계산
- 불일치를 통한 베이지안 동적 학습(Bayesian active learning by disagreement, BALD)을 사용
- 베이지안 신경망에서의 불확실성 값이 큰 샘플일수록 모델이 판단하기 어려워 훈련 데이터로 학습 시 모델 학습에 도움이 되는 샘플로 판단
- 불확실성은
드롭아웃(Dropout)을 반복적으로 수행했을때 변화하는 출력값의 분포를 통해 추정- 모델로 한 샘플에 대해 N회 반복 예측할 때마다 드롭아웃에 의해 배제되는 노드들의 바뀌면서 서로 다른 N개의 예측 확률 계산
![]()
- 모델로 한 샘플에 대해 N회 반복 예측할 때마다 드롭아웃에 의해 배제되는 노드들의 바뀌면서 서로 다른 N개의 예측 확률 계산
거리 접근
- 샘플들의 중심에서 가장 멀리 떨어진 샘플이 불확실성이 높다고 보는 방식 ->
K-means clustering사용 - 모델로부터 출력된 샘플별 특성 벡터으로부터 군집화르르 통해 중앙값을 확인하고 이 중앙값에서 가장 멀리 떨어진 샘플 선택
![]()
4. 실험 결과
4.1 평가지표 & 4.2 실험 조건
- 평가 지표
F1-score: 다중 클래스 분류에서 널리 사용되는 지표로, 클래스 불균형이 심한 상황에서 유용하게 사용
- 실험 조건
- 손실 함수 :
cross entropy - 모델의 최적화 알고리즘 :
RMSProp - 하이퍼 파라미터 :
learning_rate: 0.0005,momentum: 0.3,L2 정규화 상수: 0.0001 - 최초 훈련 데이터는 1,714매(6개 클래스)로 시작하여 매 phase마다 100매씩 추가로 50phase 진행
- 각 phase별 300 epoch
- validation loss가 25번 개선된 변화가 없으면
조기 종료(early stopping)
- 모델 성능 평가는 모든 클래스가 존재하는 테스트 데이터(전체의 20%, 9개 클래스)
- 초기에 모델이 신규 패턴을 감지하지 못하는 경우 예측 활률을 0으로 처리
- 모든 실험은 샘플링 전략마다 난수 설정을 바꿔가며 10회 반복하여 평균값 사용
- 손실 함수 :
4.3 실험 결과
4.3.1 분류 성능 결과


- 최초 구축된 모델은 분류 성능이 부족하지만, phase를 반복하며 훈련 데이터를 쌓을수록 성능 향상
- 무작위 샘플링 전략은 훈련데이터가 늘어도 성능 향상 저조
- 다른 샘플링 전략은 무작위 샘플링 대비 성능이 빠르게 향상되어 최종적으로도 더 높은 분류 성능 기록

- 모수가 많은
None,Center패턴에서는 최초부터 높은 분류 성능을 보이고 샘플링 전략 간 유의차 미약 Edge-Loc,Edge-Ring,Loc과 같은 패턴에서는 샘플링 전략을 통해 더 높은 성능 확보Scratch와 같이 수가 적은 클래스 패턴의 경우 성능의 유의차가 더욱 큼

- 신규 패턴의 경우 액티브 러닝에 따라 업데이트된 샘플 양에 의존하기 때문에 성능차가 더욱 큼
- 본 연구에서 제안하는 방법론은 20 phase 이내 구간에서 빠른 속도로 신규 패턴에 대한 성능 향상
- 샘플링 전략에 의해 감지된 신규 패턴 샘플이 훈련 데이터로 다수 업데이트되었기 때문
- 샘플링 전략이 신규 패턴 검출에 효과적으로 사용 가능
4.3.2 Train Data(Labeled) Count

- 6개의 각 샘플링 전략별로 훈련 데이터를 업데이트함에 따라 증가하는 각 클래스별 훈련 모수 표시
- 최초 모델 시 1,714매로 시작하여 phase마다 100매씩 늘려갈 때, 어떤 클래스의 샘플로 업데이트 했는가에 따라 비율이 달라짐
- 무작위 샘플링의 경우 처음 none 패턴이 모수의 대부분을 차지하며, phase가 진행되어도 최초의 클래스 비율이 유지
- none 패턴이 훈련 데이터의 대부분을 차지하고 극소수인 신규 패턴에 대한 업데이트는 거의 x
- 제안하는 샘플링 방법론에서는 none이 아닌 클래스의 비율이 확연하게 증가
- 극소수의 신규 패턴도 훈련 데이터로 다수 업데이트되는 것을 확인 가능
- none 패턴이 훈련 데이터의 대부분을 차지하고 극소수인 신규 패턴에 대한 업데이트는 거의 x
5. 결론
- 공정 내에서 발생하는 신규 패턴에 대해 그것을 인지하지 못하면 큰 품질 사고로 이어질 가능성이 높으므로 고려 필요
- 문제가 된 웨이퍼가 어떤 이력을 가졌는지 확인하기 위해서 이러한 샘플 데이터를 확보하는 것 중요
- Active Learning을 통해 신규 패턴 샘플을 확보하면서도 실험 결과를 통해 충분히 높은 수준의 정확도 획득 가능 확인