- `지수평활(exponential smoothing)`과 `ARIMA` 모델은 시계열을 예측할 때 가장 널리 사용하는 두 가지 접근 방식
- 지수평활 모델은 추세와 계절성에 대한 설명에 기초하고, ARIMA 모델은 데이터에 나타나는 `자기상관(autocorrelation)`을 표현하는 데 목적
정상성(Stationarity)과 차분(Difference)
정상성(Stationarity)
- `정상성(stationarity)`을 나타내는 시계열은 시계열의 특징이 관측된 시간에 무관
- 추세나 계절성은 서로 다른 시간에 시계열의 값에 영향을 주기 때문에 추세나 계절성이 있는 시계열은 정상성을 나타내는 시계열이 아님
- 추세나 계절성은 없지만 주기성 행동을 가지고 있는 시계열은 정상성을 나타내는 시계열
- 주기가 고정된 길이를 갖고 있지 않아 시계열을 관측하기 전에 주기의 고점이나 저점을 확실하게 알 수 없음
- 일반적으로 정상성을 나타내는 시계열은 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않음
- 시계열이 일정한 분산을 갖고 대략적으로 평평
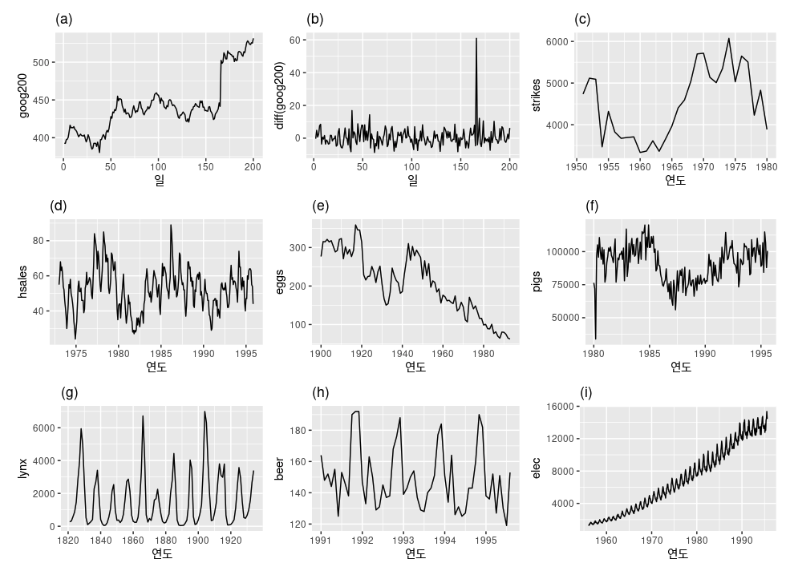
- 정상성을 나타내는 시계열
- (d), (h), (i) : 분명한 계절성을 보임
- (a), (c), (e), (f), (i) : 추세가 있고 수준이 변함
- (i) : 분산이 증가
- (g) : 뚜렷한 주기가 보이지만 이 주기는 `불규칙적(aperiodic)`이기 때문에 정상성을 나타내는 시계열
- (b) : 정상성을 나타내는 시계열
차분(Differencing)
- `차분(Differencing)`이란 연이은 관측값들의 차이를 계산하는 것
- 로그 같은 변환은 시계열의 분산 변화를 일정하게 만드는 데 도움
- 차분은 시계열의 수준에서 나타나는 변화를 제거하여 시계열의 평균 변화를 일정하게 만드는 데 도움
- 결과적으로 추세나 계절성이 제거 또는 감소
- 정상성을 나타내지 않는 시계열을 찾아낼 때 데이터의 시간 그래프뿐만 아니라 ACF 그래프도 유용
- 정상성을 나타내지 않는 데이터에서는 ACF가 느리게 감소하지만, 정상성을 나타내는 시계열에서는 빠르게 0으로 감소
- 정상성을 나타내지 않는 데이터에서 $r_1$은 종종 큰 양수 값
확률보행(random walk) 모델
- 차분을 구한 시계열은 원래의 시계열에서 연이은 관측값의 차이
- 첫 번째 관측값에 대한 차분 $\acute{y}_1$을 계산할 수 없어 차분을 구한 시계열은 $T-1$개
$$ \acute{y}_t = y_t - y_{t-1} $$
- 차분을 구한 시계열이 `백색 잡음(white noise)`라면, 원래 시계열에 대한 모델은 다음과 같음
- $\epsilon_t$는 백색 잡음을 의미
$$ y_t - y_{t-1} = \epsilon_t $$
- 이를 정리하면 `확률보행(random walk) 모델`을 얻음
$$ y_t = y_{t-1} + \epsilon_t $$
- 확률보행 모델은 정상성을 나타내지 않는 데이터, 특히 금융이나 경제 데이터를 다룰 때 널리 사용
- 확률보행 모델의 특징
- 누가봐도 알 수 있는 긴 주기를 갖는 상향 또는 하향 추세가 존재
- 갑작스럽고 예측할 수 없는 방향 변화 존재
- 미래 이동을 예측할 수 없고, 위로 갈 확률이나 아래로 갈 확률이 정확하게 같기 때문에 확률보행 모델에서 낸 예측값은 마지막 관측값과 동일
2차 차분
- 가끔 차분을 구한 데이터가 정상성이 없다고 보일 경우 한 번 더 차분을 구해 정상성을 나타내는 시계열을 얻을 수 있음
- 이 경우 $y''_t$는 $T-2$개의 값
- "변화에서 나타나는 변화"를 모델링하게 되는 셈이기 때문에 2차 차분 이상으로 구해야 하는 경우는 거의 발생 x
$$ y''_t = y'_t - y'_{t-1} = (y_t - y_{t-1}) - (y_{t-1}-y_{t-2})= y_t - 2y_{t-1} + y_{t-2} $$
계절성 차분(seasonal differencing)
- `계절성 차분(seasonal differencing)`은 관측치와, 같은 계절의 이전 관측값과의 차이
- $m$ : 계절의 개수
- $m$ 주기 시차 뒤의 관측을 빼기 때문에 시차 $m$ 차분이라고도 부름
$$ y'_t = y_t - y_{t-m} $$
- 계절성으로 차분을 구한 데이터가 `백색 잡음(white noise)`로 보일 때 원본 데이터에 대한 적절한 모델
$$ y_t = y_{t-m} + \epsilon_t
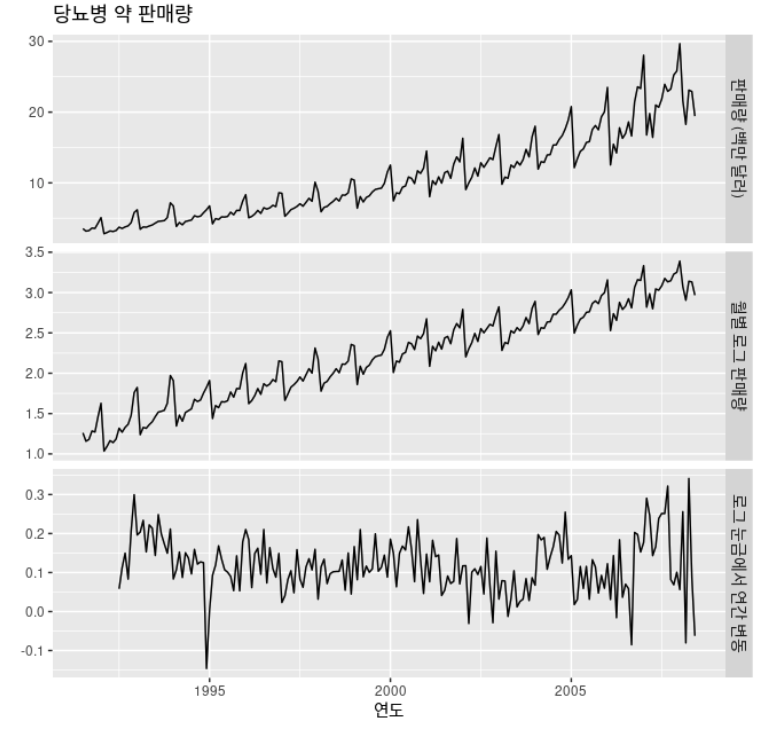
- 호주에서 팔린 A10 약물(당뇨병 약)의 월별 처방전의 수에 로그를 취하여 계절성 차분을 구한 결과
- 변환과 차분을 통해 시계열이 정상성을 나타내는 것처럼 보임
- 보통의 차분과 계절성 차분을 구분하기 위해, 보통의 차분을 시차 1에서 차분을 구한다는 의미로 `1차 차분(first difference)`라고 부름
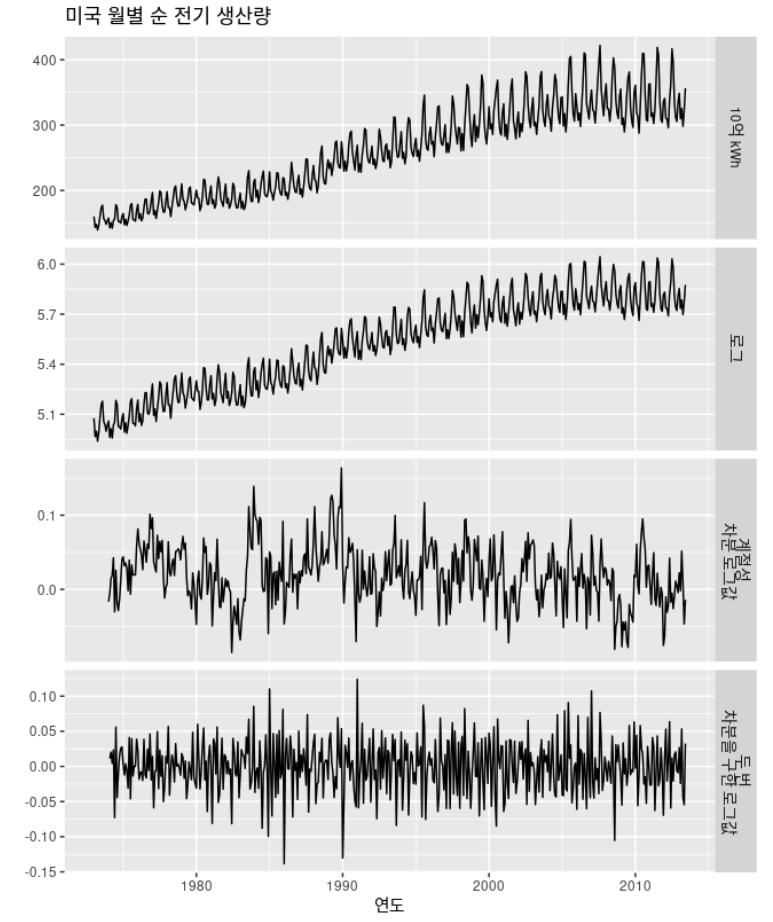
- 정상성을 나타내는 데이터를 얻기 위해 계절성 차분과 1차 차분 둘 다 구하는 것이 필요한 경우도 존재
- 아래 예시에서는 데이터를 먼저 로그로 변환하고, 계절성 차분을 계산한 후 1차 차분을 더 계산
- 어떤 차분을 구할지 정할 때는 주관적인 요소가 들어감
- 계절성 차분과 1차 차분을 둘 다 적용할 때, 어떤 것을 먼저 적용하더라도 차이 x
- 그러나 데이터에 계절성 패턴이 강하게 나타나면 계절성 차분을 먼저 계산하는 것을 추천
후방이동(Backshift) 기호
- `후방이동(backshift)` 연산자 $B$는 시계열 시차를 다룰 때 유용한 표기법
- $B$ 대신에 `시차(lag)`을 나타내는 $L$을 사용
- $y_t$에 작용하는 $B$는 데이터를 한 시점 뒤로 옮기는 효과
- 두 번 적용 시 데이터를 두 시점 뒤로 옮김
$$ B_{y_t} = y_{t-1} ##
$$ B(B_{y_t}) = B^2_{y_t} = y_{t-2} $$
- 후방이동 연산자는 차분을 구하는 과정을 설명할 때 편리
- 1차 차분은 $(1-B)$, 2차 차분은 $(1-B)^2_{y_t}로 표시
$$ y'_t = y_t - y_{t-1} = y_t - By_t = (1-B)y_t $$
$$ y''_t = y_t - 2y_{t-1} + y_{t-2} = (1-2B+B^2)y_t = (1-B)^2y_t $$
- 결론적으로 $d$차 차분은 다음과 같이 표현
$$ (1-B)^dy_t $$
- 차분을 연산자로 결합하면 보통의 대수 법칙을 사용하여 다룰 수 있게 되기 때문에, 후방이동 기호는 특별히 유용
- $B$를 포함하는 항은 서로 곱할 수 있음
자기회귀(Autoregressive) 모델
- `자기회귀(autoregressive)` 모델은 변수의 과거 값의 선형 조합을 이용하여 관심 있는 변수를 예측
- 차수 $p$의 자기회귀 모델(`AR(p)` 모델)
- $epsilon_t$ : `백색잡음(white noise)`
- $y_t$의 시차 값을 예측변수로 다루는 것을 제외하면 다중 회귀와 동일
$$ y_t = c + \phi_1y_{t-1} + \phi_2y_{t-2} + ... + \phi_py_{t-p} + \epsilon_t $$
- 자기회귀 모델은 다양한 종류의 서로 다른 시계열 패턴을 매우 유연하게 다룰 수 있음
- 매개변수 $\phi_1, ... , \phi_p$를 바꾸면 다른 시계열 패턴이 나옴
- 오차항 $\epsilon_t$의 분산은 시계열의 패턴이 아니라 눈금만 변경
- 왼쪽 그래프는 `AR(1)` 모델, 오른쪽 그래프는 `AR(2)` 모델
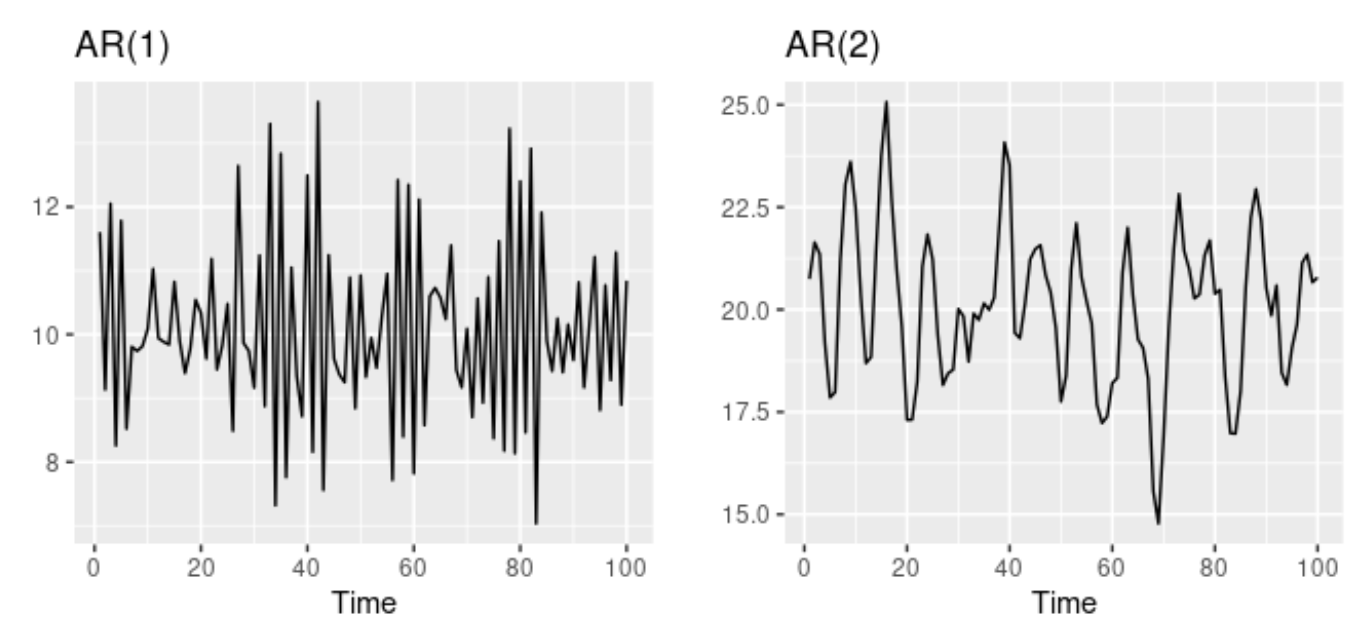
- AR(1) 모델의 특징
- $\phi_1 = 0$ : $y_t$는 백색잡음
- $\phi_1 = 1, c=0$ : $y_t$는 확률보행 모델
- $\phi_1 = 0, c\neq0$ : $y_t$는 표류가 있는 확률보행 모델
- $\phi_1 <0$ : $y_t$는 평균값을 중심으로 진동하는 경향
- 보통은 자기회귀 모델은 정상성을 나타내는 데이터에만 사용하며, 이 경우 매개변수 값에 대한 몇몇 제한 조건 필요
- AR(1) 모델 : $-1 < \phi_1 < 1$
- AR(2) 모델 : $-1 < \phi_2 < 1, \phi_1 + \phi_2 < 1, \phi_2 - \phi_1 < 1$
이동 평균(Moving Average) 모델
- `이동 평균(Moving Average)` 모델은 회귀처럼 보이는 모델에서 `과거 예측 오차(forecast eror)`을 이용
- $q$차 이동 평균 모델 `MA(q)` 모델
- $\epsilon_t$ : 백색잡음
- $\epsilon_t$가 값을 갖진 않기 때문에 실제로는 보통 생각하는 회귀 x
$$ y_t = c + \epsilon_t + \theta_1\epsilon_{t-1} + \theta_2\epsilon_{t-2} + ... + \theta_q\epsilon_{t-q} $$
- $y_t$의 각 값을 몇 개의 예측 오차의 가중 이동 평균으로 간주
- 이동 평균 모델은 미래 값을 예측할 때 사용하지만, 이동 평균 평활은 과거 값의 추세-주기 값을 측정할 때 사용
- 매개변수 $\theta_1, ... , \theta_q$를 다르게 설정한 이동 평균 모델
- 왼쪽 그래프는 `MA(1)` 모델, 오른쪽 그래프는 `MA(2)` 모델
- 오차항 $\epsilon_t$의 분산은 시계열의 패턴이 아닌 눈금만 바굼
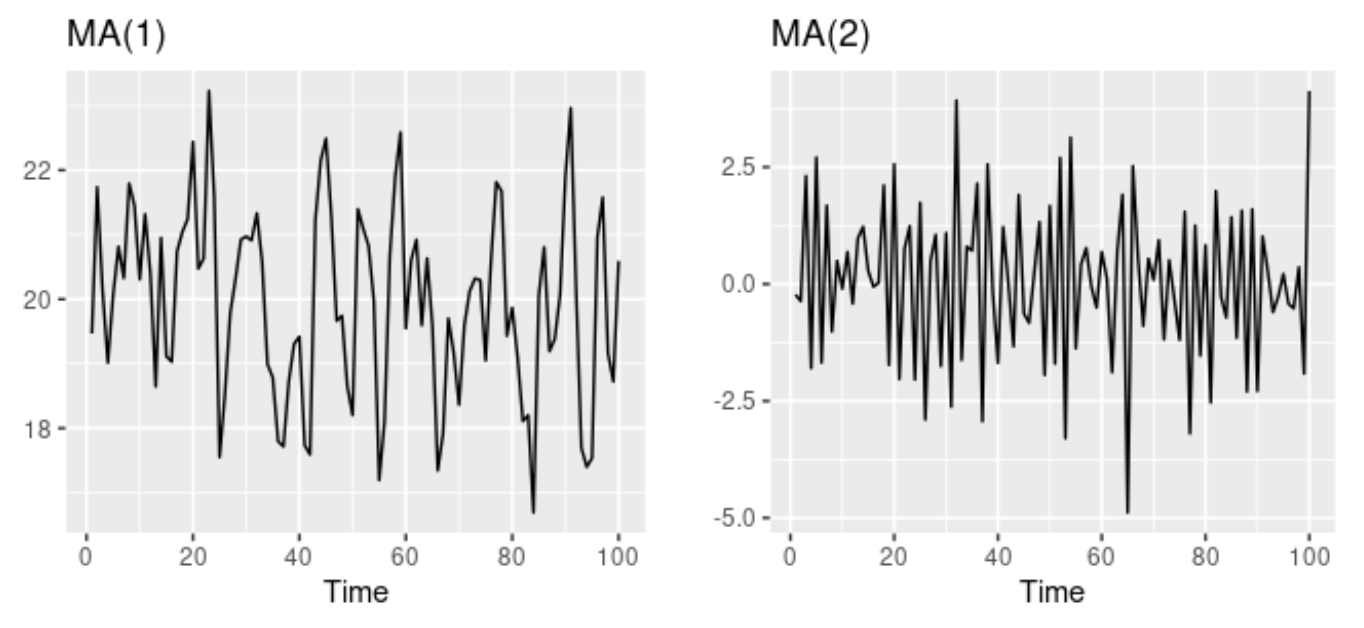
- 정상성을 나타내는 어떤 `AR(p)` 모델은 `MA($\infiny$)`로 표현
- 이동 평균 모델이 `가역적(invertible)`일 경우 `MA(q)` 모델을 `AR($\infiny$)` 모델로 표현 가능
- $\left|theta \right| > 1$이면, 가중치의 `시차(lag)` 값이 증가함에 따라 증가하고, 더 멀리 떨어진 관측값일수록 현재 오차에 미치는 영향이 커짐
- $\left|theta \right| = 1$이면, 가중치가 크기에 대해 상수이고, 멀리 떨어진 관측값과 가까운 관측값 모두 같은 영향을 끼침
- 따라서 $\left|theta \right| < 1$가 필요하고, 이는 가장 최근 관측값이 멀리 떨어진 관측값보다 더 큰 가중치를 갖음
- 이를 만족하는 이동 평균 모델은 가역적
- `가역성(invertibility)` 제한조건은 `정상성(stationarity)` 제한조건과 비슷
- `MA(1)` 모델 : $-1 < \theta_1 < 1$
- `MA(2)` 모델 : $-1 < \theta_2 < 1, \theta_2 + \theta_1 > -1, \theta_1 - \theta_2 < 1$
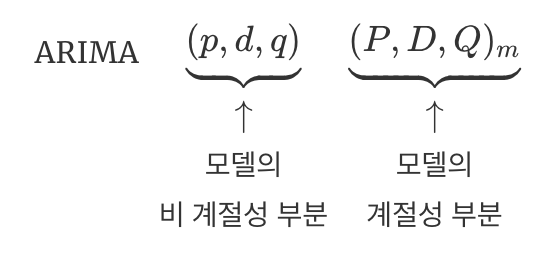
비계절성 ARIMA 모델
- 차분을 구하는 것을 자기회귀와 이동 평균 모델과 결합하면 `비계절성(non-seasonal) ARIMA` 모델을 얻음
- `ARIMA(p,d,q)` 모델 : 차분을 구한 시계열 $y'_t$로, 예측변수에 $y_t$의 시차 값과 시차 오차를 모두 포함
- $p$ : 자기회귀 부분의 차수
- $d$ : 1차 차분이 포함된 정도
- $q$ : 이동 평균 부분의 차수
$$ y'_t = c + \phi_1y'_{t-1} + ... + \phi_py'_{t-p} + \theta_1\epsilon_{t-1} + ... + \theta_q\epsilon_{t-q} + \epsilon_t \qquad (8.1) $$
- 자기회귀와 이동 평균 모델에 사용되는 정상성과 가역성 조건은 ARIMA 모델에도 적용
- 복잡한 모델을 만들기 위해 성분을 결합할 때, `후방이동(backshift)` 기호 사용
ACF와 PACF 그래프
- 단순하게 시간 그래프만 보고나서 어떤 $p$와 $q$ 값이 데이터에 맞는지 알 수 없음
- 적절한 $p$와 $q$ 값을 결정하기 위해 `ACF` 그래프와 `PACF` 그래프 이용
- `부분 자기상관값들(partial autocorrelations)`은 시차 1,2,3, ..., k-1의 효과를 제거한 후의 $y_t$와 $y_{t-k}$ 사이의 관계를 측정
- 첫 번째 부분 자기상관은 제거할 부분이 없어 첫 번째 자기상관과 동일
- 각 부분 자기상관은 자기회귀 모델의 마지막 계수처럼 측정 가능
- $k$번째 부분 자기상관 계수 $\alpha_k$ 값은 `AR(k)` 모델에서 $\phi_k$ 측정값과 동일
- 차분을 구한 데이터의 ACF와 PACF 그래프가 다음과 같은 패턴을 나타내면, 데이터는 $ARIMA(p,d,0)$ 모델일 수 있음
- ACF가 지수적으로 감소 혹은 사인 함수 모양
- PACF 그래프에서 시차 $p$에 뾰족한 막대가 유의미하게 존재하지만, 시차 $p$ 이후는 없는 경우
- 차분을 구한 데이터의 ACF와 PACF 그래프가 다음과 같은 패턴을 나타내면, 데이터는 $ARIMA(0,d,q)$ 모델일 수 있음
- PACF가 지수적으로 감소 혹은 사인 함수 모양
- ACF 그래프에서 시차 $q$에 뾰족한 막대가 유의미하게 존재하지만, 시차 $q$ 이후는 없는 경우
추정과 차수 선택
최대 가능도 추정
- 모델의 차수인 $p, d, q$ 값을 찾은 후 매개변수 $c, \phi_1, ... , \phi_p, \theta_1, ... , \theta_q$을 추정할 때 `최대 가능도 추정(maximum likelihood estimation, MLE)`을 사용
- 관찰한 데이터를 얻는 확률을 최대화하는 매개변수의 값을 찾는 방법
- ARIMA 모델에서는 MLE가 `최소제곱(least squares)` 추정과 비슷
$$ \sum_{t=1}^{T}\epsilon^2_t $$
- 실제로는 `로그 가능도(log likelihood)`, 즉 추정한 모델에서 나온 관측 데이터의 확률의 로그를 활용
정보 기준
- 아카이케의 정보 기준(AIC)이 ARIMA 모델에서 차수를 결정할 때도 유용
- $L$ : 데이터의 가능도
- $c \neq 0$이면 $k = 1$이고, $c = 0$이면 $k = 0$
- 마지막 항이 모델의 매개변수 개수
$$ AIC = -2log(L) + 2(p + q + k + 1) $$
- ARIMA 모델에 대한 수정된 AIC
$$ AIC_c = AIC + \frac{2(p+q+k+1)(p+q+k+2)}{T-p-q-k-2} $$
- 베이지안 정보 기준
$$ BIC = AIC + \left [ log(T)-2 \right ](p+q+k+1) $$
- 이러한 정보 기준은 모델의 적절한 차분 차수($d$)를 고를 때 별로 도움이 되지 않는 경향이 있고, $p$와 $q$ 값을 고를 때만 도움
- 차분을 구하는 것을 통해 가능도를 계산하는 데이터가 변경되어 서로 다른 차수로 차분을 구한 모델의 AIC 값을 비교 불가
- 따라서 $d$를 구하는 다른 방법을 사용해야 하고, $p$나 $q$를 구하기 위해 $AIC_c$를 사용
예측하기
점 예측치
- ARIMA 모델에서 점 예측값을 구하는 과정
- $y$가 좌변에 오고 다른 모든 항들이 우변에 오도록 ARIMA 식을 전개
- $t$를 $T+h$로 바꾸어 식을 다시 씀
- 식의 우변에서 미래 관측값을 예측값으로 바꾸고, 미래 오차값을 0으로 바꾸며, 과거 오차값을 해당 잔차로 바꿈
- $h=1$로 시작하여, 모든 예측값을 계산할 때까지 $h = 2,3, ...$에 대하여 위 단계를 반복
계절성 ARIMA 모델들
- 계절성 ARIMA 모델은 ARIMA 모델에 추가적인 계절성 항을 포함하여 구성
- $m$ : 매년 관측값의 개수
- 모델의 계절성 부분에 대문자 기호, 비계절성 부분에는 소문자 기호 사용
- 모델의 계절성 부분은 비계절성 성분과 비슷한 항으로 구성되지만 계절성 주기의 후방이동을 포함
- $ARIMA(1,1,1)(1,1,1)_4$ 모델, 즉 분기별 데이터($m=4$)에 대한 경우
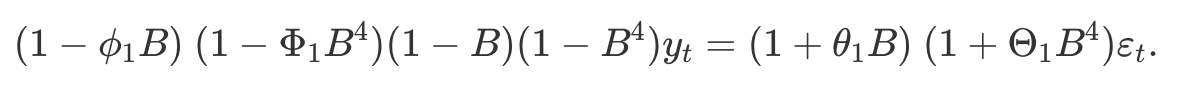
ACF/PACF
- AR이나 MA 모델의 계절성 부분은 PACF와 ACF의 계절성 시차에서 확인
- 계절성 ARIMA 모델에서 적절한 계절성 차수를 고려할 때, 계절성 시차를 고려
- 모델링 과정은 모델의 비계절성 성분과 계절성 AR과 MA 항을 골라야 하는 것을 제외하고는 비계절성 데이터와 거의 동일
유럽 분기별 소매 거래 예제
- 1996년부터 2011년까지 분기별 유럽 소매 거래 데이터를 이용하여 계절성 ARIMA 모델링 과정 설명
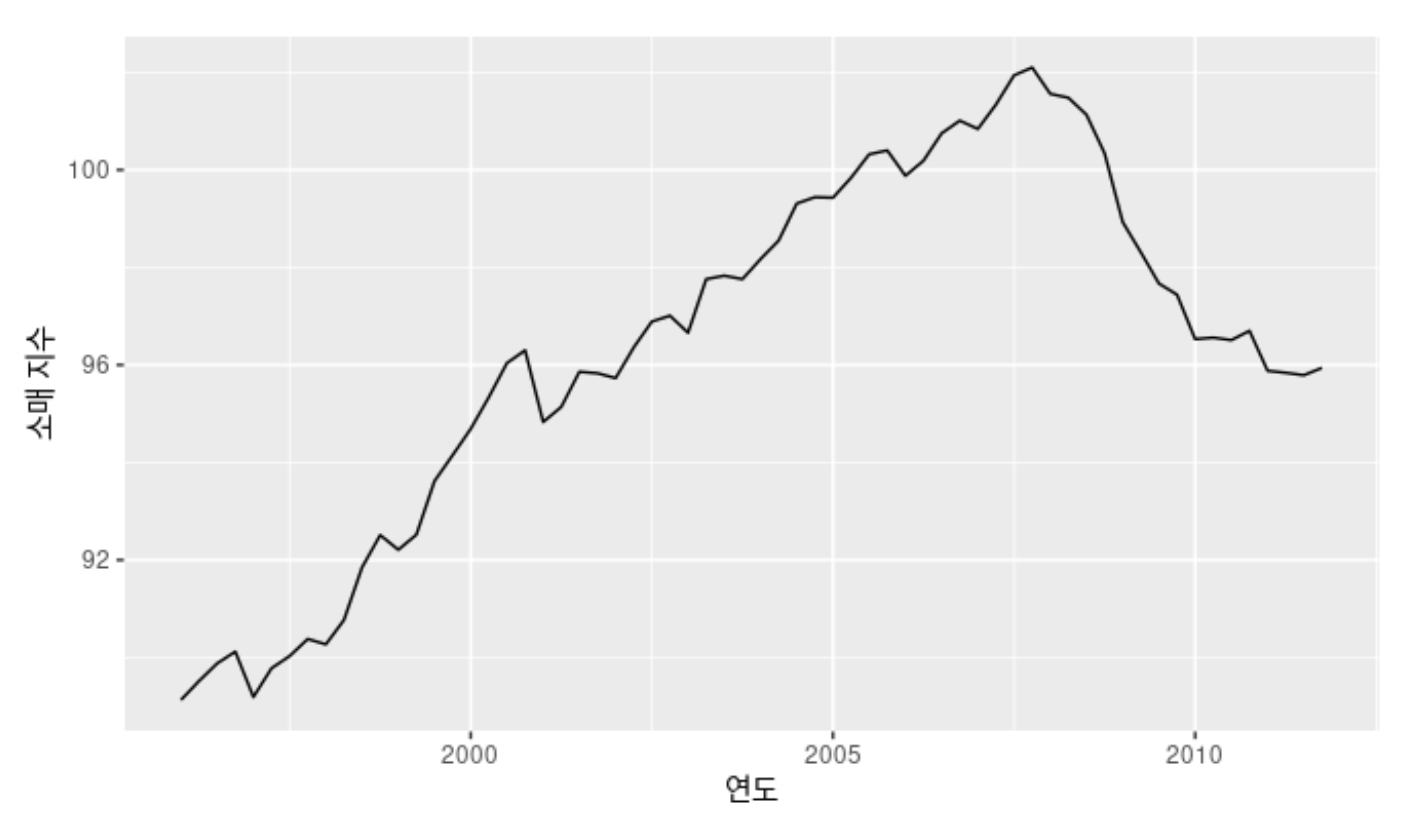
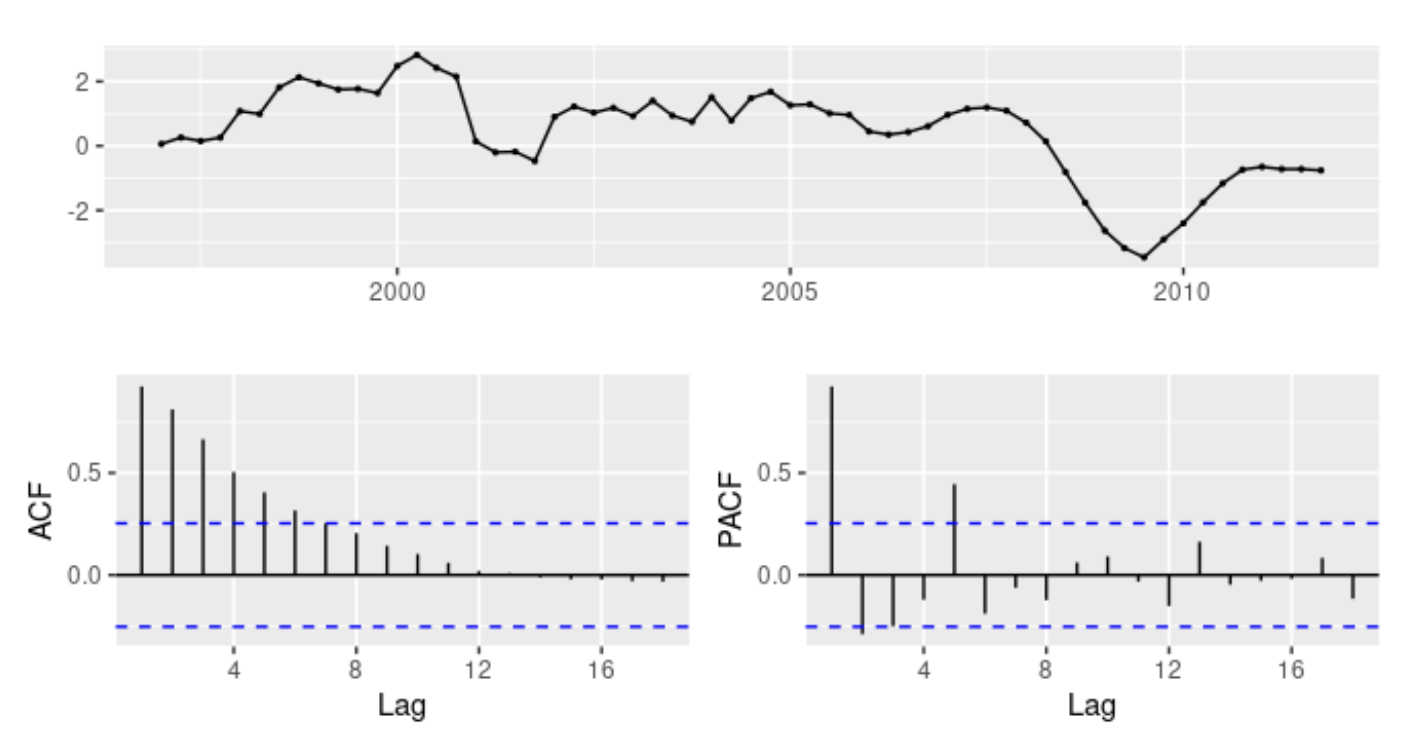
- 데이터가 정상성을 나타내지 않으면서 약간의 계절성을 보여 계절성 차분을 구함(좌)
- 아직 정상성을 나타내지 않는거 같아 1차 차분을 한 번 더 구함(우)
- ACF에서 시차 1의 유의미하게 뾰족한 막대가 비계절성 MA(1) 성분을 암시
- ACF에서 시차 4의 유의미하게 뾰족한 막대는 계절성 MA(1) 성분을 암시
- 이를 통해 1차 차분과 계절성 차분을 나타내는 $ARIMA(0,1,1)(0,1,1)_4$ 모델과 비계절성 MA(1) 성분을 가지고 시작
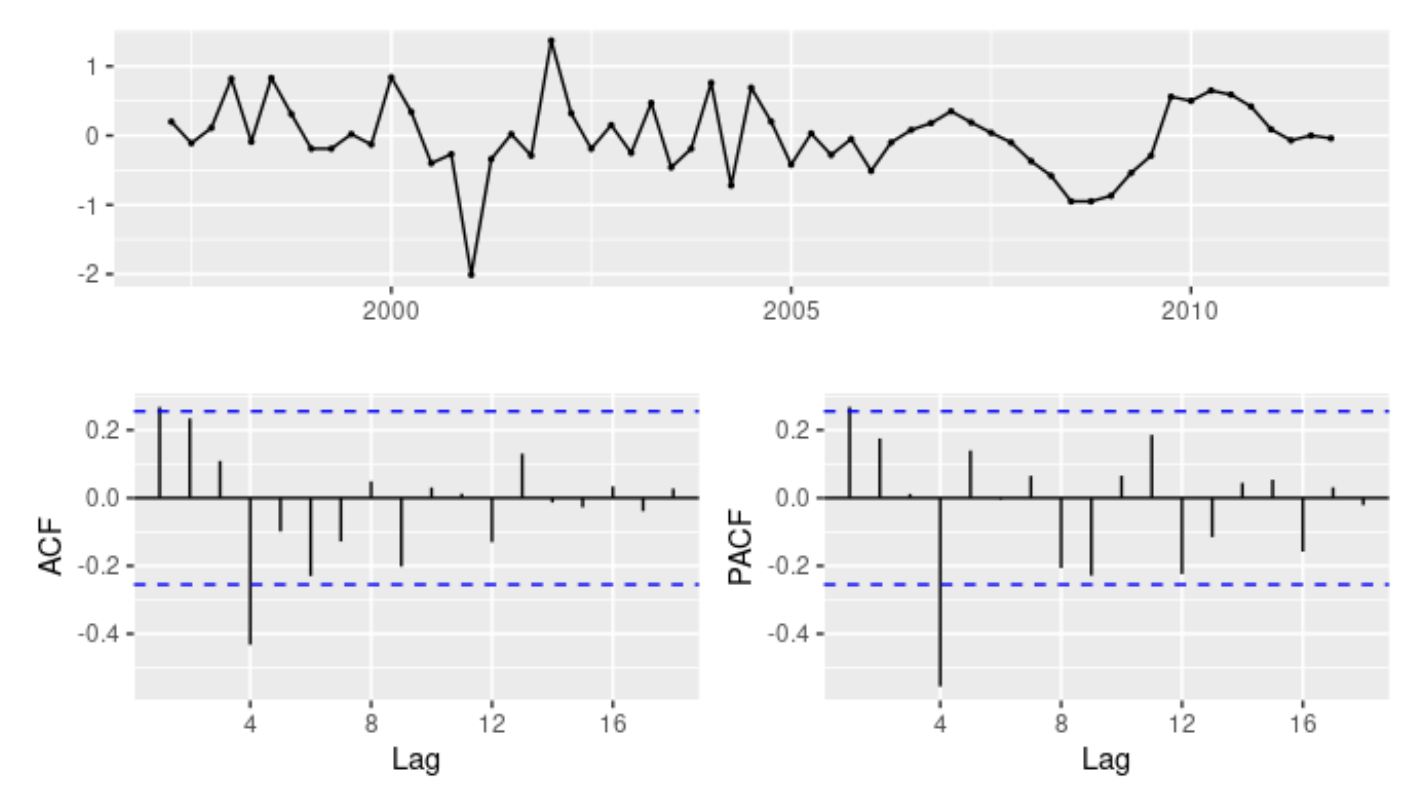
- 위의 모델에 대한 잔차
- ACF와 PACF 둘 다 시차 2에서 유의미하게 뾰족한 막대가 나타나고 시차 3에서 덜 유의미하지만 뾰족한 막대가 나타남
- 이는 몇몇 추가적인 비계절성 항이 모델에 추가되어야 한다는 것을 의미
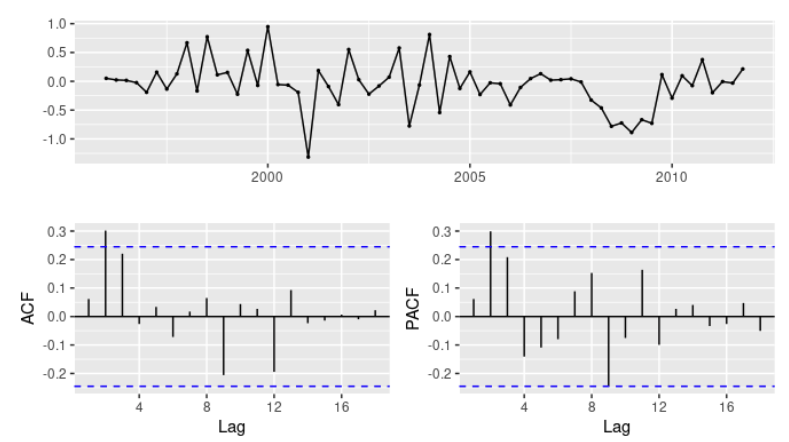
- $ARIMA(0,1,3)(0,1,1)_4$ 모델의 $AIC_c$ 값은 68.54, $ARIMA(0,1,2)(0,1,1)_4$ 모델의 $AIC_c$는 74.36
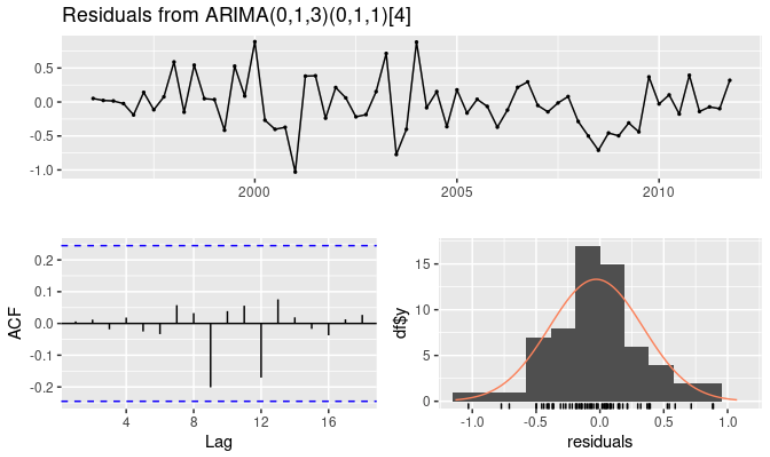
- 결론적으로 $ARIMA(0,1,3)(0,1,1)_4$ 모델을 선택하여 해당 모델의 잔차 확인
- 모든 뾰족한 막대가 유의미한 범위 안에 들어오고, 잔차는 백색잡음처럼 보임
ARIMA vs ETS
- ARIMA 모델이 지수평활보다 더 일반적이라는 것은 근거없는 믿음
- 선형 지수 평활 모델이 ARIMA 모델의 특수한 경우이지만, 비선형 지수 평활 모델은 ARIMA에 대응 x
- 반면 많은 ARIMA 모델은 지수평활에 대응 x
- 모든 ETS 모델은 정상성을 나타내지 않는 경우에 맞지만, 몇몇 ARIMA 모델은 정상성을 나타내는 경우에 맞음
- 계절성이나 비감쇠 추세 아니면 둘 다 있는 ETS 모델은 2개의 `단위근(unit root)`을 갖어 정상성을 나타내도록 하려면 2번 차분
- 다른 모든 ETS 모델은 1개의 단위근(1번 차분)
- ETS와 ARIMA 모델 사이의 동치 관계

- $AIC_c$는 같은 범주에 속하는 모델을 고르는데 유용하지만, ETS와 ARIMA 모델은 서로 다른 모델 범주에 속해 사용 x