목차
-
단순 지수평활(Simple Exponential Smoothing)
-
가중 평균 형태
-
성분 형태
-
평평한 예측값
-
최적화
-
추세 기법
-
홀트의 선형 추세 기법
-
감쇠 추세 기법
-
홀트-윈터스의 계절성 기법
-
홀트-윈터스의 덧셈 기법
-
홀트-윈터스의 곱셈 기법
-
홀트-윈터스의 감쇠 기법
-
지수 평활 기법 분류 체계
-
지수 평활에 대한 혁신 상태 공간 모델
-
ETS(A,N,N) : 덧셈 오차를 이용하는 단순 지수평활
-
ETS(M,N,N) : 곱셈 오차를 이용하는 단순 지수평활
-
ETS(A,A,N) : 덧셈 오차를 이용한 홀트의 선형 기법
-
ETS(M,A,N) : 곱셈 오차를 이용하는 홀트의 선형 기법
-
다른 ETS 모델
-
추정과 모델 선택
-
모델 선택
-
ETS 모델로 예측하기
-
예측구간(prediction interval)
-
Reference
지수 평활(exponential smoothing)을 사용하여 얻은 예측값은 과거 관측값의가중평균(weighted average)- 과거 관측값은 오래될수록 지수적으로 감소하는 가중치를 갖으며, 가장 최근 관측값이 가장 높은 가중치를 갖음
- 이러한 방식으로 다양한 종류의 시계열을 가지고 신뢰할만한 예측 작업을 빠르게 수행할 수 있으며, 이는 산업 분야에 응용할 때 매우 중요한 부분
단순 지수평활(Simple Exponential Smoothing)
- 지수적으로 평활하는 기법 중에서 가장 단순한 방법을
단순 지수평활(simple exponential smoothing, SES)라고 함 - 추세나 계절성이 없는 데이터를 예측할 때 사용하기 좋음
- 단순 지수평활 기법의 기본 개념은 오래된 관측값보다 더 최근 관측값에 더 큰 가중치를 주는 것
- 더 오래될수록 가중치가 지수적으로 감소하는 방식으로 예측치를 계산
- alpha : 0부터 1사이 값으로 평활 매개변수
- 시간 T+1에 대한
one-step-ahead forecast는 모든 관측값을 가중 평균하여 얻은 값 - 가중치가 감소하는 비율은 매개변수 alpha로 조절
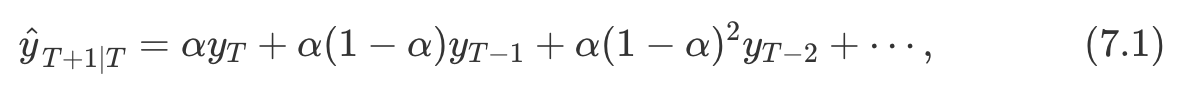
- 단순 지수 평활로 예측할 때 서로 다른 alpha로 관측값에 할당할 경우, 작은 alpha 값이라도 가중치의 합은 근사적으로 1
- alpha가 0에 가깝다면 더 먼 과거 관측값에 붙는 가중치가 늘어나며, 1에 가까운 경우 더 최근 관측값에 붙는 가중치가 늘어남
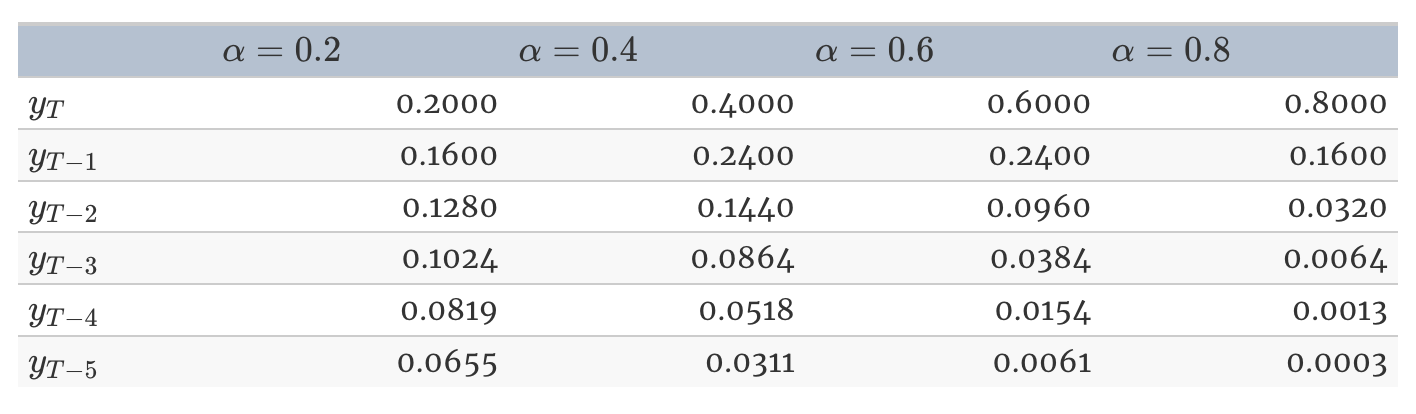
가중 평균 형태
- 식 (7.1)을 유도하는 2가지 동일한 형태의 단순 지수평활(가중 평균 형태, 성분 형태)
- 시간 T+1의 예측은 가장 최근값과 이전 예측값의 가중평균과 동일
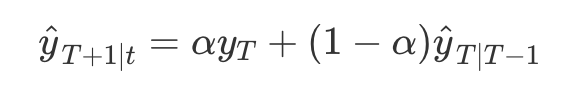
- 비슷하게
적합값(fitted value)또한 다음과 같이 표현이 가능- 여기에서의 적합값은 단순히 학습 데이터의 한 단계 예측(one-step forecast)
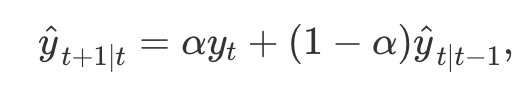
- 진행 과정을 시작하기 위해 우리가 추정해야할 시간 1에서의 첫 번째 적합값을 l_0으로 표현
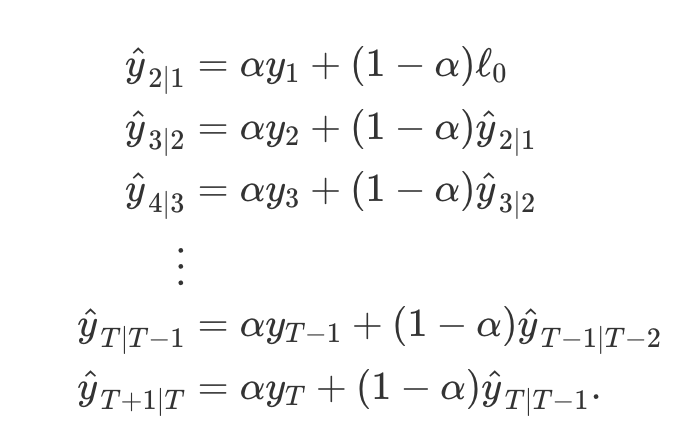
- 이를 각 식에 대입하면 가중 평균 형태로 예측식 (7.1)을 표현
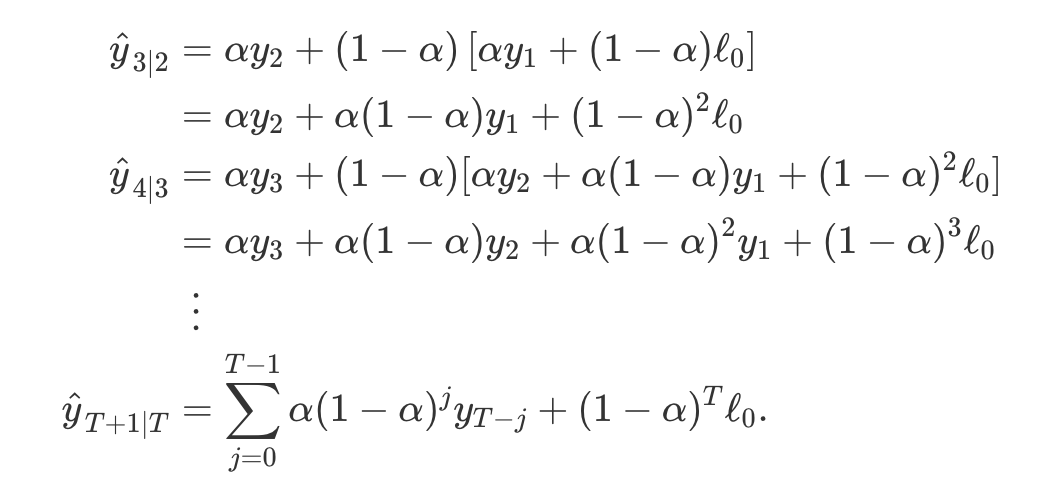
성분 형태
- 단순 지수평활에서 포함된 유일한 성분은 수준값 l_t
- 지수 평활 기법의 성분 형태 표현은 기법에 포함된 각 성분에 대한 예측식과 평활식으로 구성
- l_t : 시간 t에서의 시계열의 수준값(또는 평활화된 값)
- h = 1로 두면 적합값을 얻을 수 있고, t = T로 두면 학습 데이터 이후의 예측값을 얻을 수 있음
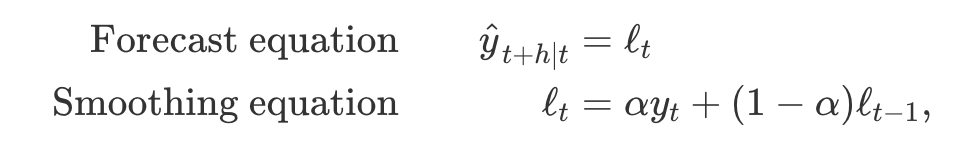
- 단순 지수 평활의 성분 형태는 특별히 유용하진 않지만, 다른 성분을 추가할 때 가장 쉽게 사용할 수 있는 형태
평평한 예측값
- 단순 지수 평활은
평평(flat)한 예측 함수를 갖음- 모든 예측값이 마지막 수준 성분과 같은 값을 갖음
- 이러한 예측은 시계열에 추세나 계절 성분이 없을 때 사용할 수 있음
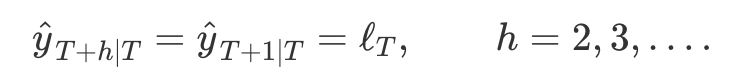
최적화
- 모든 지수 평활법을 응용할 때는 평활 매개변수와 초기값이 필요하며, 이를 알면 데이터로부터 모든 예측치를 계산 가능
- 단순 지수평활의 경우 alpha와 l_0를 선택
- 평활 매개변수를 주관적으로 선택하는 경우 예측하는 사람이 이전의 경험에 근거하여 평활 매개변수의 값을 정함
- 알려지지 않는 매개변수 값을 얻는 더욱 안전하고 객관적인 방법은 관측된 데이터에서 이러한 값을 추정하는 것
잔차(residual)의 제곱의 합을 최소화하여 회귀 모델의 계수를 추정한 것과 비슷하게, SSE를 최소화하여 매개변수와 초기값을 구할 수 있음- 잔차 e_t = y_t - y^_t | t-1로 명시
- SSE를 최소화하는 회귀 계수값을 돌려받는 공식이 있는 회귀 모델과는 다르게, 이 경우 비선형 최소화 문제이기 때문에 최적화 도구를 사용해 최소화
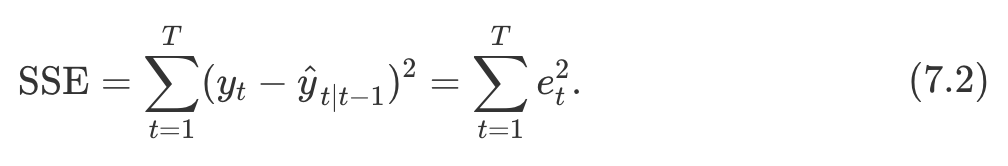
추세 기법
홀트의 선형 추세 기법
- 추세가 있는 데이터를 예측할 수 있도록 예측식과 두 개의 평활식(각각 수준, 추세에 관한 것)을 포함해 단순 지수 평활을 확장
- l_t : 시간 t에서 시계열의 수준 추정 값
- b_t : 시간 t에서의 시계열의 추세(기울기) 추정 값
- alpha : 0부터 1 사이의 수준에 대한 매개변수
- beta : 0부터 1 사이의 추세에 대한 매개변수
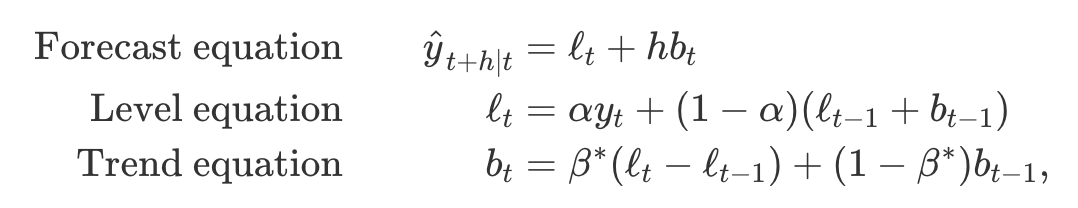
수준식(level equation)은 l_t가 관측 y_t의 가중 평균이며, l_t-1 + b_t-1로 주어지는 시간 t에 대한한 단계 앞 학습 예측(one-step-ahead training forecast)라는 것을 나타냄추세식(trend equation)은 b_t가 추세의 이전 추정 값인 l_t - l_t-1와 b_t-1에 기초한, 시간 t에서의 추정된 추세의 이동 평균이라는 것을 나타냄- 예측 함수는 더이상 평평하지 않고, 추세를 가짐
- h단계 앞 예측은 마지막 추정 수준에 마지막 추정 추세값의 h배 한 것을 더한 값
- 예측값은 h의 선형 함수
감쇠 추세 기법
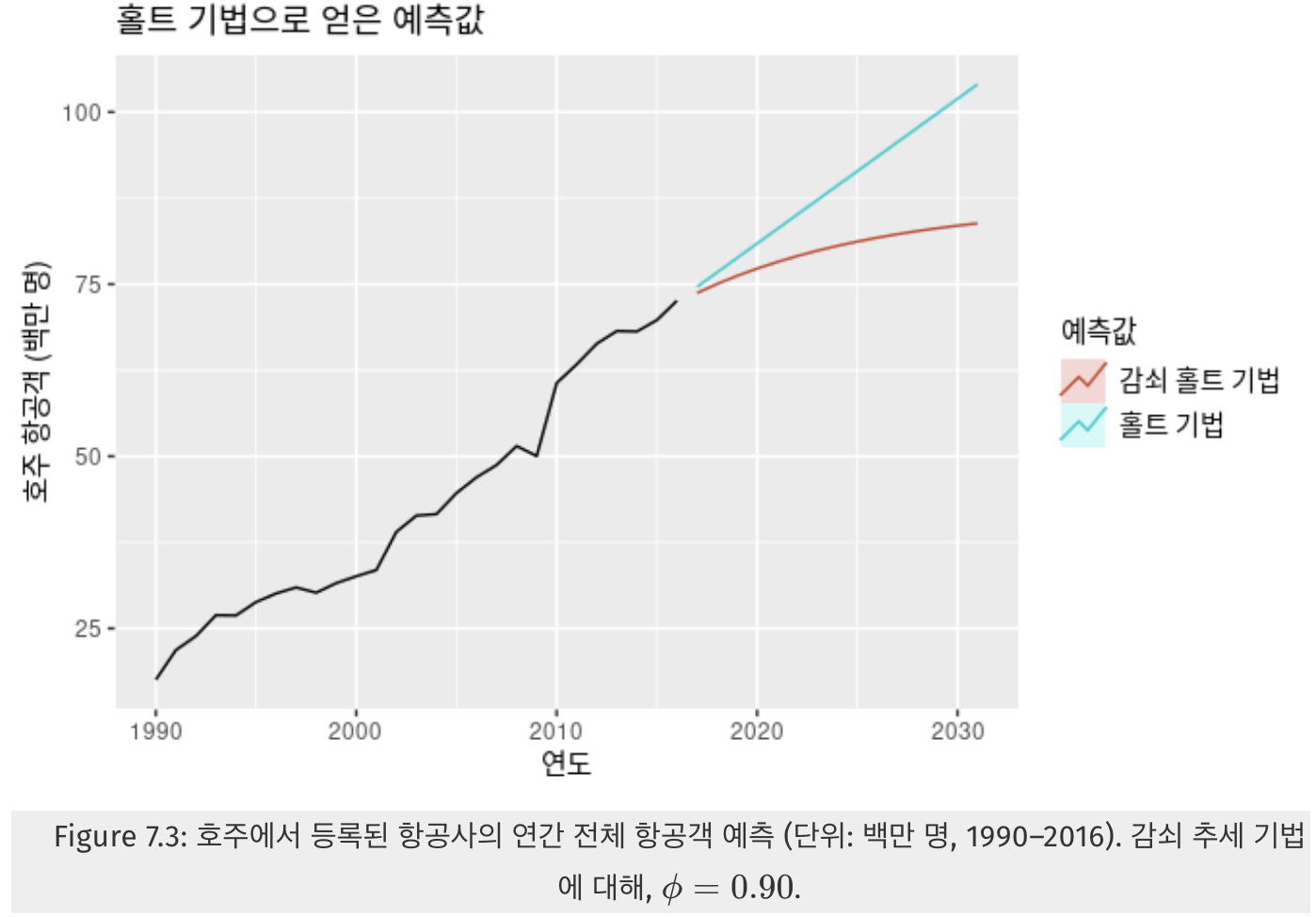
- 홀트의 선형 기법으로 얻은 예측값은 미래에도 계쏙 일정한 증가 또는 감소 추세를 나타내 이는 과도하게 예측하는 경향이 있다고 알려짐
- 미래 어느 시점에 추세를 평평하게 감쇠시키는 한 가지 매개변수인
감쇠하는 추세(damped trend)를 추가로 도입- 이는 매우 성공적이라는 것이 증명되었으며, 자동으로 예측하는 일이 필요한 많은 시계열에서 가장 인기 있는 기법
- 평활 매개변수 alpha와 beta 외에도 감쇠 매개변수 phi를 도입
- phi = 1이면 홀트의 선형 기법과 동일
- 0과 1 사이의 값에 대해 phi는 추세를 감쇠시켜 미래 어떤 시점에 추세가 상수가 되도록 함
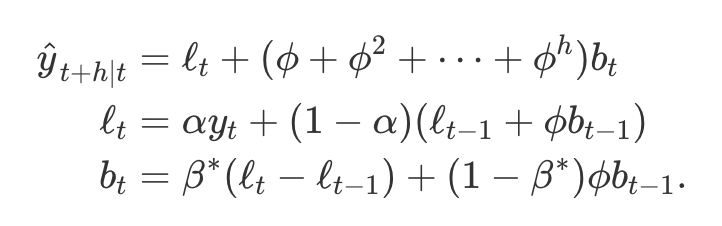
- phi가 작을수록 감쇠 효과가 매우 강하게 들어가므로 실제 상황에서 phi가 0.8보다 작은 경우는 드뭄
- 보통 phi의 최소값을 0.8로 잡고 최대값을 0.98로 제한
홀트-윈터스의 계절성 기법
홀트-윈터스(Holt-Winters) 계절성 기법은 수준 l_t, 추세 b_t, 계절 성분 s_t에 대한 3개의 평활식으로 구성되며, 각각은 대응되는 평활 매개변수로 이루어짐- 계절 성분의 성질에 따라 덧셈 기법과 곱셈 기법에 해당하는 두 가지 변형 존재
- 덧셈 기법은 계절성 변동이 시계열 전반에 걸쳐 거의 일정할 때 사용
- 곱셈 기법은 계절성 변동이 시계열의 수준에 비례하게 변할 때 사용
- 덧셈 기법에서 계절성분은 관측된 시계열의 척도로 나타내고, 수준식에서 계절성분을 빼서 시계열을 계절성으로 조절
- 곱셈 기법에서 계절성분은 상대적인 항(백분율)으로 표현하고, 시계열은 계절성분으로 나누어 계절성으로 조절
홀트-윈터스의 덧셈 기법
- 덧셈 기법에 대한 성분 형태
- k는 (h-1)/m의 정수 부분으로, 예측을 위해 계절성 지수를 추정한 값이 표본의 마지막 연도에서 유래하도록 함
- 수준식은 계절성으로 조정된 관측값(y_t - s_t-m)과 시간 t에 대한 비계절성 예측(y_t - l_t-1 - b_t-1)을 나타냄
- 계절성식은 현재 계절성 지수(y_t - l_t-1 - b_t-1)와 이전 연도 같은 계절(m 시점 이전)의 계절성 지표 사이의 가중 평균
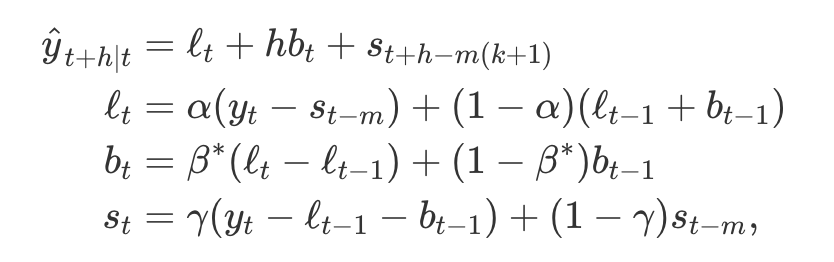
- 계절성식은 종종 다음과 같이 나타냄
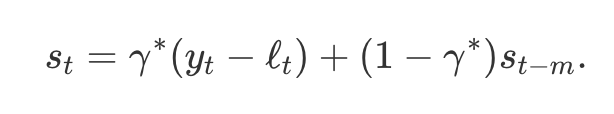
홀트-윈터스의 곱셈 기법
- 곱셈 기법에 대한 성분 형태
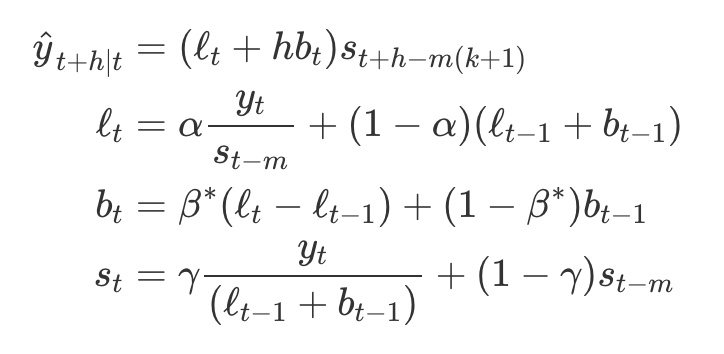
홀트-윈터스의 감쇠 기법
- 홀트-윈터스의 덧셈과 곱셈 기법 두 경우 모두 감쇠 효과를 추가 가능
- 계절성 데이터에 대해 정확하고 안정적인 예측치를 내는 한 가지 기법은 다음과 같이 홀트-윈터스에
감쇠 추세(damped trend)와곱셈 계절성(multiplicative seasonality)를 고려한 것
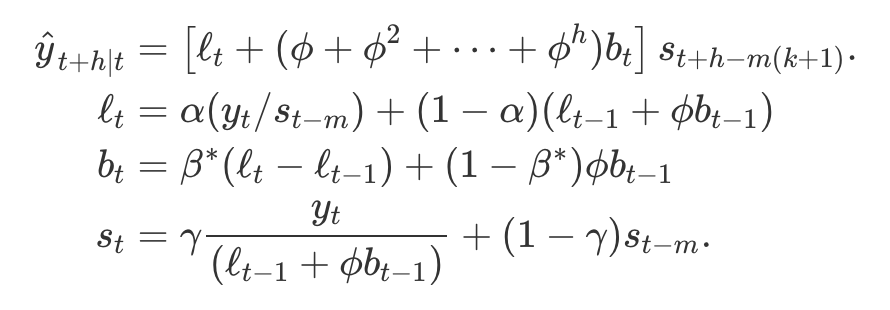
지수 평활 기법 분류 체계
- 지수 평활기법의 추세와 계절적인 성분의 조합을 고려해보면 총 15가지의 지수 평활 기법이 가능
- (A, M)은 덧셈 추세(Additive trend)와 곱셈 계절성(Multiplicative seasonality)을 사용하는 기법
- (A_d, N)은 감쇠 추세(damped trend)와 계절성이 없는 기법
- 곱셈 감쇠 기법은 나쁜 예측치를 내는 경향이 있어 다루지 않음
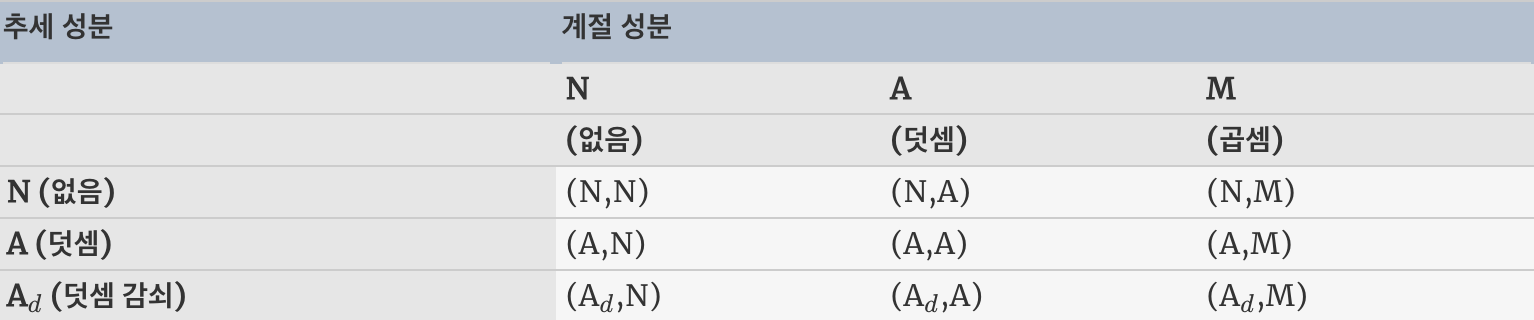
- 9가지 지수 평활 기법을 적용하기 위한 재귀식
- 표의 각 칸에는 h 단계 앞 예측값을 내는 예측식과 기법을 적용하기 위한 평활식이 포함

지수 평활에 대한 혁신 상태 공간 모델
- 통계 모델이란 전체 예측분포를 만들어줄 수 있는 무작위적 데이터 생성 과정
- 각 모델은 관측된 데이터를 묘사하는
측정식(measurement equation)과, 아직 관측되지 않은 성분이나 상태(수준, 추세, 계절성)가 시 에 따라 어떻게 변하는지 나타내는 몇 가지상태식(state equation)으로 구성- 따라서
상태 공간 모델(state space models)이라고 부름
- 따라서
- 각 기법마다 각각 덧셈 오차, 곱셈 오차를 이용하는 두 가지 모델이 존재
- 같은 평활 매개변수 값을 사용했다면, 모델의 점 예측은 동일하지만 다른 예측 구간을 생성
- 덧셈 오차와 곱셈 오차를 사용하는 모델을 구분하고, 기법에서 모델을 구분하기 위해 지수 평활의 분류에 세 번째 문자 하나를 더 추가
- (오차Error, 추세Trend, 계절성Seasonal)에 대해 각 상태 공간 모델을 ETS(·,·,·)로 나타냄
- ETS를 ExponenTial Smoothing이라고도 생각할 수 있음
ETS(A,N,N) : 덧셈 오차를 이용하는 단순 지수평활
- 단순 지수평활의 성분 식을 다시 정리하면
오차 보정(error correction)식을 얻음- e_t = y_t - l_t-1 = y_t - y^_t|t-1는 시간 t에서의
잔차(residual)
- e_t = y_t - l_t-1 = y_t - y^_t|t-1는 시간 t에서의
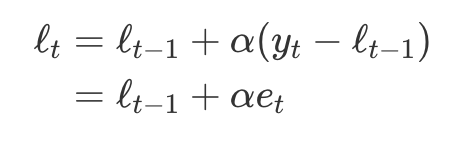
- 훈련 데이터 오차는 시간 t에 대한 평활 과정에 걸쳐 추정된 수준의 조정으로 이어짐
- 시간 t에서 오차가 음수이면, y_t < y^_t|t-1이고 따라서 시간 (t-1)에서 수준은 과도하게 추정
- 그러면 새로운 수준 l_t은 하향 조정된 이전 수준 l_t-1이 됨
- alpha가 1에 가까울수록 수준 추정이 더 고르지 않아 큰 조정이 일어남
- alpha가 작을수록, 수준이 더 고르게 되어 작은 조정이 일어남
- 각 관측값이 이전 수준에 오차를 더한 것과 같게 두기 위해 다음과 같이 식을 쓸 수도 있음
혁신 상태 공간 모델(innovation state space model)로 만들기 위해, e_t의 확률분포를 식으로 구체적으로 표현- 덧셈 오차를 이용하는 모델에 대해, 잔차(한 단계 학습 오차) e_t가 평균이 0이면서 분산이 sigma^2인 정규분포를 따라는
백색잡음(white noise)로 가정 - NID는 정규적, 독립적으로 분포된(Normally and Independently Distributed)를 줄여 쓴 것
- 식 (7.3)은 측정(관측) 방정식, 식 (7.4)는 상태(전이) 방정식

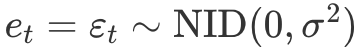
혁신(innovations)이라는 단어는 모든 식이 같은 무작위 오차 가정을 사용한다는 사실에서 유래- 측정 방정식은 관측값과 아직 관측되지 않은 상태와의 관계를, 상태 방정식은 시간에 따른 상태의 면화를 나타냄
ETS(M,N,N) : 곱셈 오차를 이용하는 단순 지수평활
- 같은 방식으로 한 단계 앞 학습 오차를 상대적인 오차로 써서 곱셈 오차를 사용하는 모델
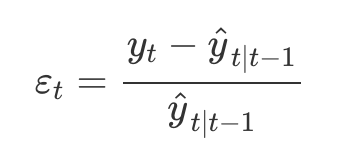
- 상태 공간 모델의 곱셈 형태
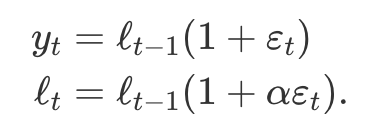
ETS(A,A,N) : 덧셈 오차를 이용한 홀트의 선형 기법
- 한 단계 앞 학습 오차
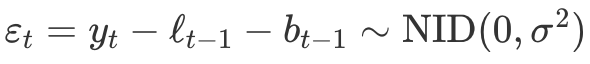
- 홀트의 선형 기법에 대한 오차 보정식에 대입
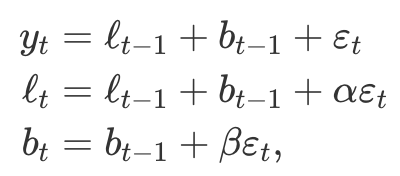
ETS(M,A,N) : 곱셈 오차를 이용하는 홀트의 선형 기법
- 한 단계 앞 학습 오차
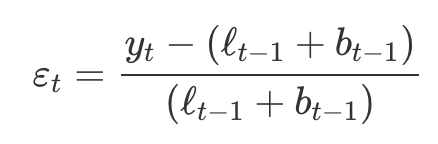
- 곱셈 오차를 이용하는 홀트의 선형 기법을 이루는 혁신 상태 공간 모델
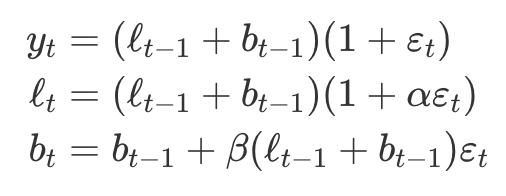
다른 ETS 모델

추정과 모델 선택
- 가능도는 특정한 모델에서 일어나는 데이터의 확률이기 때문에 큰 가능도는 좋은 모델과 관련 있음
- 덧셈 오차 모델의 경우 가능도를 최대화하면 제곱 오차의 합을 최소화하는 것과 결과 동일(오차가 정규 분포를 따른다는 가정 하에)
- 곱셈 오차 모델의 경우 서로 다른 결과
- 가능도를 최대화하여 평활 매개변수와 초기 상태를 구함
- 평활 매개변수는 관련 식이 가중평균으로 해석될 수 있도록 가질 수 있는 값의 범위를 0과 1 사이로 제한
모델 선택
- 모델을 선택할 때 정보 기준(
AIC,AIC_c,BIC)을 사용할 수 있다는 것은 ETS 통계 체제의 큰 장점 - ETS 모델의 아카이케의 정보 기준(AIC)
- L은 모델의 가능도
- k는 잔차 분산을 포함하여 추정되는 매개변수와 초기 상태의 전체 개수
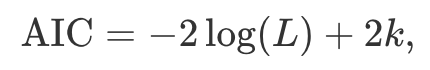
- 작은 표본에 대해 보정된 AIC(AIC_c)
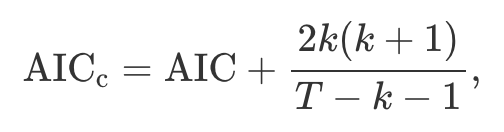
- 베이지안 정보 기준(BIC)
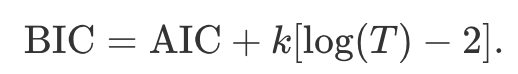
- (오차, 추세, 계절성)의 세 가지 성분의 조합에서 수치적으로 어려운 부분이 생길 수 있음
- ETS(A,N,M), ETS(A,A,M), ETS(A,A_d,M) 모델에서 불안정성을 일으킬 수 있음
- 상태 식에서 0에 가까운 값으로 나눌 수도 있기 때문
- 이런 특정 조합은 모델을 선택할 때 보통 고려 x
- 곱셈 오차를 이용하는 모델은 데이터가 분명하게 양수일 때는 유용하지만, 데이터에 0이나 음수 값이 있으면 수치적으로 불안정
- 곱셈 오차 모델은 시계열이 분명하게 양수가 아닐 때는 사용 x
- 이러한 경우 덧셈 오차만 이용하는 6가지 모델만 적용
ETS 모델로 예측하기
- t = T+1, ... , T+h에 대한 식을 가지고 반복하고 t > T에 대해 모두 epsilon_t = 0으로 둬 점 예측값을 얻음
- ETS 점 예측값은 예측 분포의
중간값(median)과 동일- 덧셈 성분만 이용하는 모델의 경우 예측 분포가 정규분포이기 때문에 평균과 중앙값이 동일
- 곱셈 오차를 이용하는 ETS 모델의 경우나 곱셈 계절성을 이용하는 경우 점 예측값은 예측분포의 평균값과 같지 않음
예측구간(prediction interval)
- 대부분의 ETS 모델에 대해
예측구간(prediction interval)은 다음과 같이 정의- k :
포함확률(coverage probability)에 따라 달라짐 - sigma_h : 예측 분산
- k :
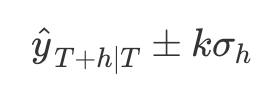
- 각각의 덧셈 상태 공간 모델에 대한 예측 분산 식
- sigma^2 : 잔차 분산
- m : 계절성 주기
- k : (h-1)/m의 정수 부분(시간 T+h 앞 예측 기간에서 연도의 개수)

Reference
지수 평활(exponential smoothing)을 사용하여 얻은 예측값은 과거 관측값의가중평균(weighted average)- 과거 관측값은 오래될수록 지수적으로 감소하는 가중치를 갖으며, 가장 최근 관측값이 가장 높은 가중치를 갖음
- 이러한 방식으로 다양한 종류의 시계열을 가지고 신뢰할만한 예측 작업을 빠르게 수행할 수 있으며, 이는 산업 분야에 응용할 때 매우 중요한 부분
단순 지수평활(Simple Exponential Smoothing)
- 지수적으로 평활하는 기법 중에서 가장 단순한 방법을
단순 지수평활(simple exponential smoothing, SES)라고 함 - 추세나 계절성이 없는 데이터를 예측할 때 사용하기 좋음
- 단순 지수평활 기법의 기본 개념은 오래된 관측값보다 더 최근 관측값에 더 큰 가중치를 주는 것
- 더 오래될수록 가중치가 지수적으로 감소하는 방식으로 예측치를 계산
- alpha : 0부터 1사이 값으로 평활 매개변수
- 시간 T+1에 대한
one-step-ahead forecast는 모든 관측값을 가중 평균하여 얻은 값 - 가중치가 감소하는 비율은 매개변수 alpha로 조절
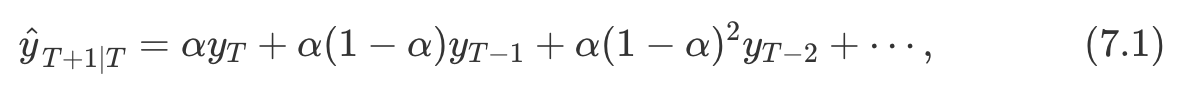
- 단순 지수 평활로 예측할 때 서로 다른 alpha로 관측값에 할당할 경우, 작은 alpha 값이라도 가중치의 합은 근사적으로 1
- alpha가 0에 가깝다면 더 먼 과거 관측값에 붙는 가중치가 늘어나며, 1에 가까운 경우 더 최근 관측값에 붙는 가중치가 늘어남

가중 평균 형태
- 식 (7.1)을 유도하는 2가지 동일한 형태의 단순 지수평활(가중 평균 형태, 성분 형태)
- 시간 T+1의 예측은 가장 최근값과 이전 예측값의 가중평균과 동일
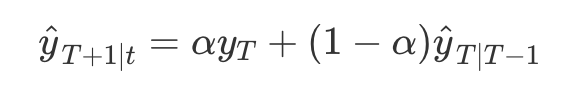
- 비슷하게
적합값(fitted value)또한 다음과 같이 표현이 가능- 여기에서의 적합값은 단순히 학습 데이터의 한 단계 예측(one-step forecast)
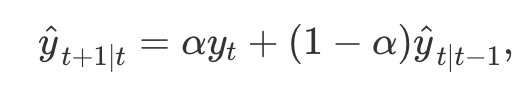
- 진행 과정을 시작하기 위해 우리가 추정해야할 시간 1에서의 첫 번째 적합값을 l_0으로 표현
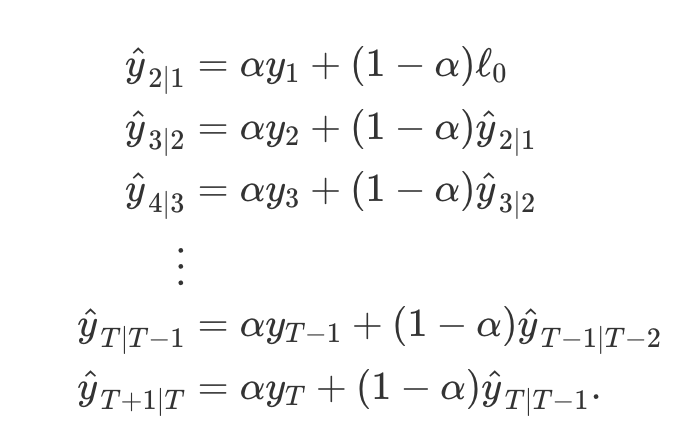
- 이를 각 식에 대입하면 가중 평균 형태로 예측식 (7.1)을 표현
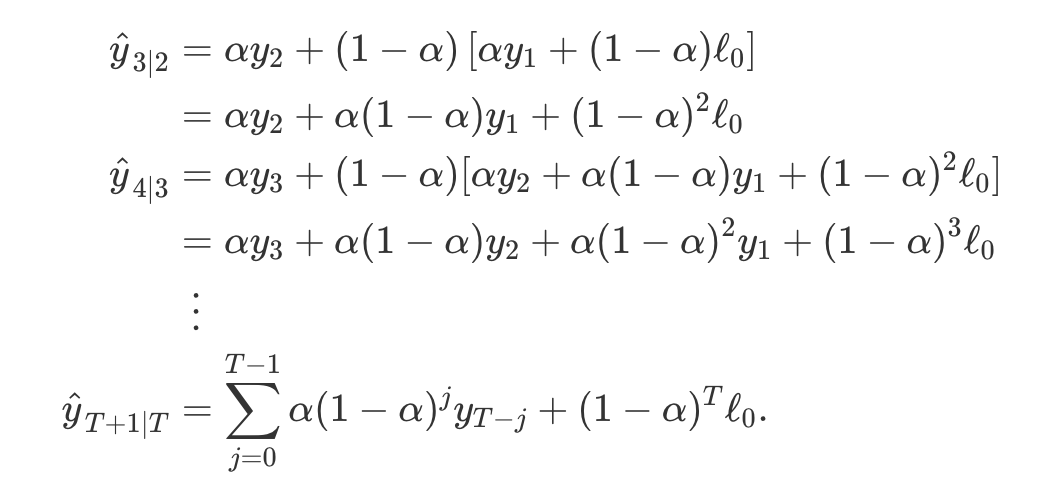
성분 형태
- 단순 지수평활에서 포함된 유일한 성분은 수준값 l_t
- 지수 평활 기법의 성분 형태 표현은 기법에 포함된 각 성분에 대한 예측식과 평활식으로 구성
- l_t : 시간 t에서의 시계열의 수준값(또는 평활화된 값)
- h = 1로 두면 적합값을 얻을 수 있고, t = T로 두면 학습 데이터 이후의 예측값을 얻을 수 있음
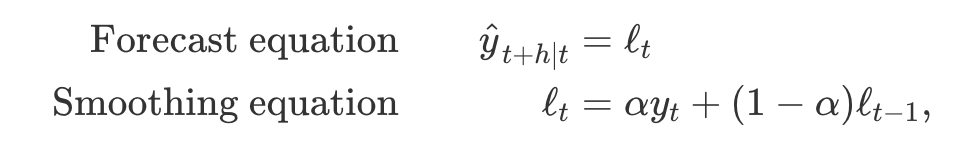
- 단순 지수 평활의 성분 형태는 특별히 유용하진 않지만, 다른 성분을 추가할 때 가장 쉽게 사용할 수 있는 형태
평평한 예측값
- 단순 지수 평활은
평평(flat)한 예측 함수를 갖음- 모든 예측값이 마지막 수준 성분과 같은 값을 갖음
- 이러한 예측은 시계열에 추세나 계절 성분이 없을 때 사용할 수 있음
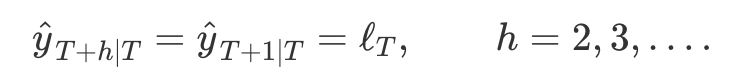
최적화
- 모든 지수 평활법을 응용할 때는 평활 매개변수와 초기값이 필요하며, 이를 알면 데이터로부터 모든 예측치를 계산 가능
- 단순 지수평활의 경우 alpha와 l_0를 선택
- 평활 매개변수를 주관적으로 선택하는 경우 예측하는 사람이 이전의 경험에 근거하여 평활 매개변수의 값을 정함
- 알려지지 않는 매개변수 값을 얻는 더욱 안전하고 객관적인 방법은 관측된 데이터에서 이러한 값을 추정하는 것
잔차(residual)의 제곱의 합을 최소화하여 회귀 모델의 계수를 추정한 것과 비슷하게, SSE를 최소화하여 매개변수와 초기값을 구할 수 있음- 잔차 e_t = y_t - y^_t | t-1로 명시
- SSE를 최소화하는 회귀 계수값을 돌려받는 공식이 있는 회귀 모델과는 다르게, 이 경우 비선형 최소화 문제이기 때문에 최적화 도구를 사용해 최소화
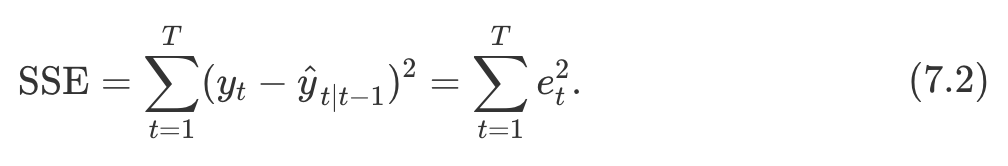
추세 기법
홀트의 선형 추세 기법
- 추세가 있는 데이터를 예측할 수 있도록 예측식과 두 개의 평활식(각각 수준, 추세에 관한 것)을 포함해 단순 지수 평활을 확장
- l_t : 시간 t에서 시계열의 수준 추정 값
- b_t : 시간 t에서의 시계열의 추세(기울기) 추정 값
- alpha : 0부터 1 사이의 수준에 대한 매개변수
- beta : 0부터 1 사이의 추세에 대한 매개변수
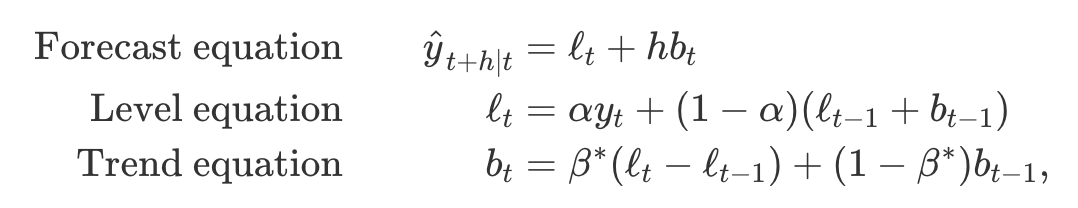
수준식(level equation)은 l_t가 관측 y_t의 가중 평균이며, l_t-1 + b_t-1로 주어지는 시간 t에 대한한 단계 앞 학습 예측(one-step-ahead training forecast)라는 것을 나타냄추세식(trend equation)은 b_t가 추세의 이전 추정 값인 l_t - l_t-1와 b_t-1에 기초한, 시간 t에서의 추정된 추세의 이동 평균이라는 것을 나타냄- 예측 함수는 더이상 평평하지 않고, 추세를 가짐
- h단계 앞 예측은 마지막 추정 수준에 마지막 추정 추세값의 h배 한 것을 더한 값
- 예측값은 h의 선형 함수
감쇠 추세 기법
- 홀트의 선형 기법으로 얻은 예측값은 미래에도 계쏙 일정한 증가 또는 감소 추세를 나타내 이는 과도하게 예측하는 경향이 있다고 알려짐
- 미래 어느 시점에 추세를 평평하게 감쇠시키는 한 가지 매개변수인
감쇠하는 추세(damped trend)를 추가로 도입- 이는 매우 성공적이라는 것이 증명되었으며, 자동으로 예측하는 일이 필요한 많은 시계열에서 가장 인기 있는 기법
- 평활 매개변수 alpha와 beta 외에도 감쇠 매개변수 phi를 도입
- phi = 1이면 홀트의 선형 기법과 동일
- 0과 1 사이의 값에 대해 phi는 추세를 감쇠시켜 미래 어떤 시점에 추세가 상수가 되도록 함
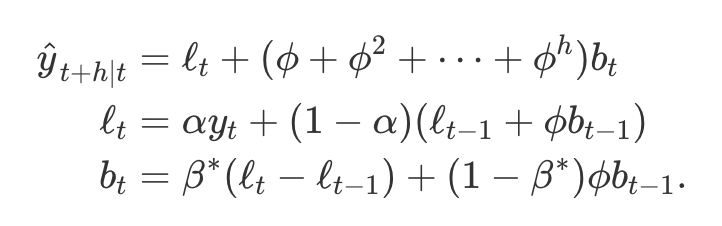
- phi가 작을수록 감쇠 효과가 매우 강하게 들어가므로 실제 상황에서 phi가 0.8보다 작은 경우는 드뭄
- 보통 phi의 최소값을 0.8로 잡고 최대값을 0.98로 제한

홀트-윈터스의 계절성 기법
홀트-윈터스(Holt-Winters) 계절성 기법은 수준 l_t, 추세 b_t, 계절 성분 s_t에 대한 3개의 평활식으로 구성되며, 각각은 대응되는 평활 매개변수로 이루어짐- 계절 성분의 성질에 따라 덧셈 기법과 곱셈 기법에 해당하는 두 가지 변형 존재
- 덧셈 기법은 계절성 변동이 시계열 전반에 걸쳐 거의 일정할 때 사용
- 곱셈 기법은 계절성 변동이 시계열의 수준에 비례하게 변할 때 사용
- 덧셈 기법에서 계절성분은 관측된 시계열의 척도로 나타내고, 수준식에서 계절성분을 빼서 시계열을 계절성으로 조절
- 곱셈 기법에서 계절성분은 상대적인 항(백분율)으로 표현하고, 시계열은 계절성분으로 나누어 계절성으로 조절
홀트-윈터스의 덧셈 기법
- 덧셈 기법에 대한 성분 형태
- k는 (h-1)/m의 정수 부분으로, 예측을 위해 계절성 지수를 추정한 값이 표본의 마지막 연도에서 유래하도록 함
- 수준식은 계절성으로 조정된 관측값(y_t - s_t-m)과 시간 t에 대한 비계절성 예측(y_t - l_t-1 - b_t-1)을 나타냄
- 계절성식은 현재 계절성 지수(y_t - l_t-1 - b_t-1)와 이전 연도 같은 계절(m 시점 이전)의 계절성 지표 사이의 가중 평균
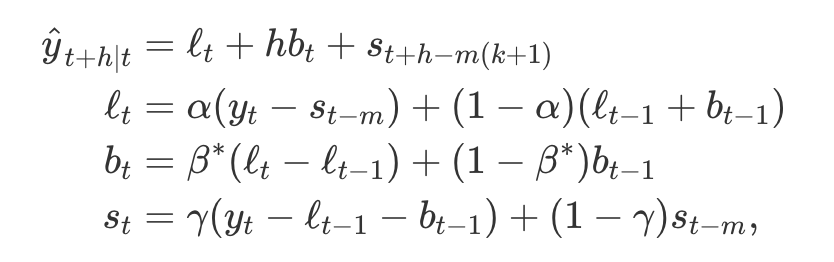
- 계절성식은 종종 다음과 같이 나타냄
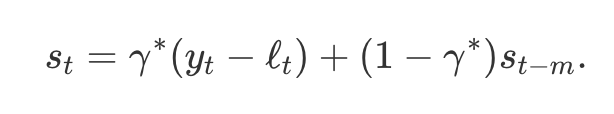
홀트-윈터스의 곱셈 기법
- 곱셈 기법에 대한 성분 형태
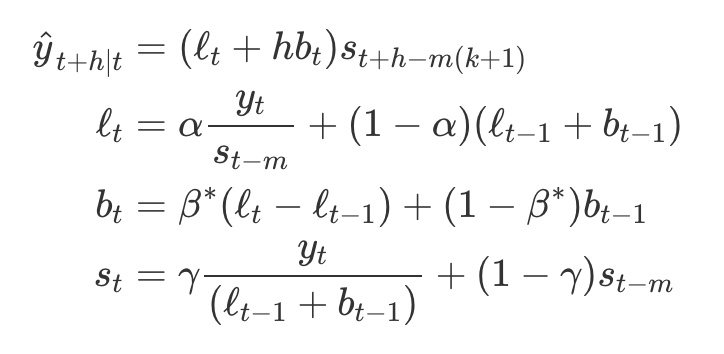
홀트-윈터스의 감쇠 기법
- 홀트-윈터스의 덧셈과 곱셈 기법 두 경우 모두 감쇠 효과를 추가 가능
- 계절성 데이터에 대해 정확하고 안정적인 예측치를 내는 한 가지 기법은 다음과 같이 홀트-윈터스에
감쇠 추세(damped trend)와곱셈 계절성(multiplicative seasonality)를 고려한 것
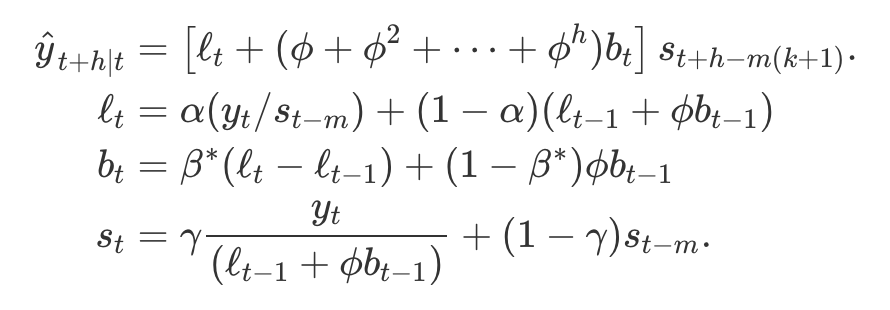
지수 평활 기법 분류 체계
- 지수 평활기법의 추세와 계절적인 성분의 조합을 고려해보면 총 15가지의 지수 평활 기법이 가능
- (A, M)은 덧셈 추세(Additive trend)와 곱셈 계절성(Multiplicative seasonality)을 사용하는 기법
- (A_d, N)은 감쇠 추세(damped trend)와 계절성이 없는 기법
- 곱셈 감쇠 기법은 나쁜 예측치를 내는 경향이 있어 다루지 않음

- 9가지 지수 평활 기법을 적용하기 위한 재귀식
- 표의 각 칸에는 h 단계 앞 예측값을 내는 예측식과 기법을 적용하기 위한 평활식이 포함

지수 평활에 대한 혁신 상태 공간 모델
- 통계 모델이란 전체 예측분포를 만들어줄 수 있는 무작위적 데이터 생성 과정
- 각 모델은 관측된 데이터를 묘사하는
측정식(measurement equation)과, 아직 관측되지 않은 성분이나 상태(수준, 추세, 계절성)가 시 에 따라 어떻게 변하는지 나타내는 몇 가지상태식(state equation)으로 구성- 따라서
상태 공간 모델(state space models)이라고 부름
- 따라서
- 각 기법마다 각각 덧셈 오차, 곱셈 오차를 이용하는 두 가지 모델이 존재
- 같은 평활 매개변수 값을 사용했다면, 모델의 점 예측은 동일하지만 다른 예측 구간을 생성
- 덧셈 오차와 곱셈 오차를 사용하는 모델을 구분하고, 기법에서 모델을 구분하기 위해 지수 평활의 분류에 세 번째 문자 하나를 더 추가
- (오차Error, 추세Trend, 계절성Seasonal)에 대해 각 상태 공간 모델을 ETS(·,·,·)로 나타냄
- ETS를 ExponenTial Smoothing이라고도 생각할 수 있음
ETS(A,N,N) : 덧셈 오차를 이용하는 단순 지수평활
- 단순 지수평활의 성분 식을 다시 정리하면
오차 보정(error correction)식을 얻음- e_t = y_t - l_t-1 = y_t - y^_t|t-1는 시간 t에서의
잔차(residual)
- e_t = y_t - l_t-1 = y_t - y^_t|t-1는 시간 t에서의
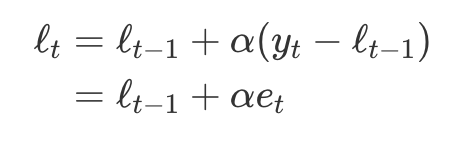
- 훈련 데이터 오차는 시간 t에 대한 평활 과정에 걸쳐 추정된 수준의 조정으로 이어짐
- 시간 t에서 오차가 음수이면, y_t < y^_t|t-1이고 따라서 시간 (t-1)에서 수준은 과도하게 추정
- 그러면 새로운 수준 l_t은 하향 조정된 이전 수준 l_t-1이 됨
- alpha가 1에 가까울수록 수준 추정이 더 고르지 않아 큰 조정이 일어남
- alpha가 작을수록, 수준이 더 고르게 되어 작은 조정이 일어남
- 각 관측값이 이전 수준에 오차를 더한 것과 같게 두기 위해 다음과 같이 식을 쓸 수도 있음
혁신 상태 공간 모델(innovation state space model)로 만들기 위해, e_t의 확률분포를 식으로 구체적으로 표현- 덧셈 오차를 이용하는 모델에 대해, 잔차(한 단계 학습 오차) e_t가 평균이 0이면서 분산이 sigma^2인 정규분포를 따라는
백색잡음(white noise)로 가정 - NID는 정규적, 독립적으로 분포된(Normally and Independently Distributed)를 줄여 쓴 것
- 식 (7.3)은 측정(관측) 방정식, 식 (7.4)는 상태(전이) 방정식

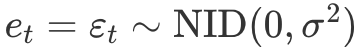
혁신(innovations)이라는 단어는 모든 식이 같은 무작위 오차 가정을 사용한다는 사실에서 유래- 측정 방정식은 관측값과 아직 관측되지 않은 상태와의 관계를, 상태 방정식은 시간에 따른 상태의 면화를 나타냄
ETS(M,N,N) : 곱셈 오차를 이용하는 단순 지수평활
- 같은 방식으로 한 단계 앞 학습 오차를 상대적인 오차로 써서 곱셈 오차를 사용하는 모델
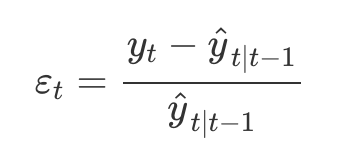
- 상태 공간 모델의 곱셈 형태
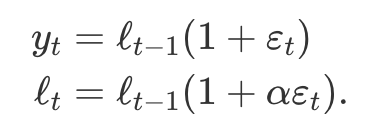
ETS(A,A,N) : 덧셈 오차를 이용한 홀트의 선형 기법
- 한 단계 앞 학습 오차
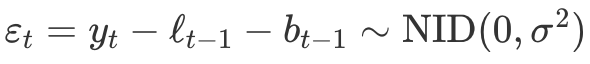
- 홀트의 선형 기법에 대한 오차 보정식에 대입
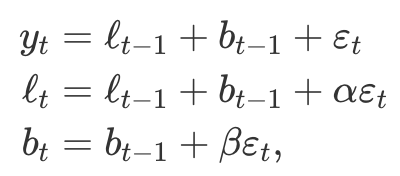
ETS(M,A,N) : 곱셈 오차를 이용하는 홀트의 선형 기법
- 한 단계 앞 학습 오차
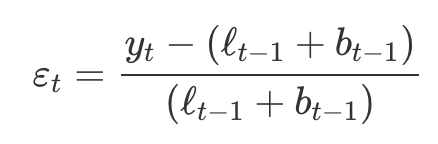
- 곱셈 오차를 이용하는 홀트의 선형 기법을 이루는 혁신 상태 공간 모델
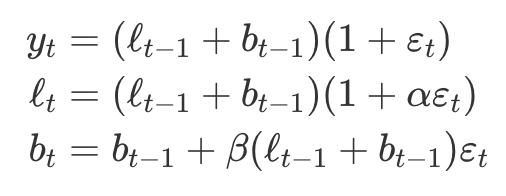
다른 ETS 모델

추정과 모델 선택
- 가능도는 특정한 모델에서 일어나는 데이터의 확률이기 때문에 큰 가능도는 좋은 모델과 관련 있음
- 덧셈 오차 모델의 경우 가능도를 최대화하면 제곱 오차의 합을 최소화하는 것과 결과 동일(오차가 정규 분포를 따른다는 가정 하에)
- 곱셈 오차 모델의 경우 서로 다른 결과
- 가능도를 최대화하여 평활 매개변수와 초기 상태를 구함
- 평활 매개변수는 관련 식이 가중평균으로 해석될 수 있도록 가질 수 있는 값의 범위를 0과 1 사이로 제한
모델 선택
- 모델을 선택할 때 정보 기준(
AIC,AIC_c,BIC)을 사용할 수 있다는 것은 ETS 통계 체제의 큰 장점 - ETS 모델의 아카이케의 정보 기준(AIC)
- L은 모델의 가능도
- k는 잔차 분산을 포함하여 추정되는 매개변수와 초기 상태의 전체 개수
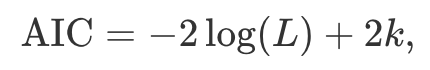
- 작은 표본에 대해 보정된 AIC(AIC_c)
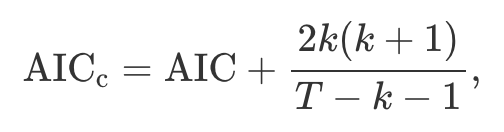
- 베이지안 정보 기준(BIC)
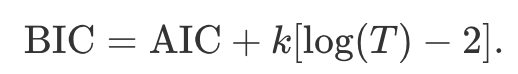
- (오차, 추세, 계절성)의 세 가지 성분의 조합에서 수치적으로 어려운 부분이 생길 수 있음
- ETS(A,N,M), ETS(A,A,M), ETS(A,A_d,M) 모델에서 불안정성을 일으킬 수 있음
- 상태 식에서 0에 가까운 값으로 나눌 수도 있기 때문
- 이런 특정 조합은 모델을 선택할 때 보통 고려 x
- 곱셈 오차를 이용하는 모델은 데이터가 분명하게 양수일 때는 유용하지만, 데이터에 0이나 음수 값이 있으면 수치적으로 불안정
- 곱셈 오차 모델은 시계열이 분명하게 양수가 아닐 때는 사용 x
- 이러한 경우 덧셈 오차만 이용하는 6가지 모델만 적용
ETS 모델로 예측하기
- t = T+1, ... , T+h에 대한 식을 가지고 반복하고 t > T에 대해 모두 epsilon_t = 0으로 둬 점 예측값을 얻음
- ETS 점 예측값은 예측 분포의
중간값(median)과 동일- 덧셈 성분만 이용하는 모델의 경우 예측 분포가 정규분포이기 때문에 평균과 중앙값이 동일
- 곱셈 오차를 이용하는 ETS 모델의 경우나 곱셈 계절성을 이용하는 경우 점 예측값은 예측분포의 평균값과 같지 않음
예측구간(prediction interval)
- 대부분의 ETS 모델에 대해
예측구간(prediction interval)은 다음과 같이 정의- k :
포함확률(coverage probability)에 따라 달라짐 - sigma_h : 예측 분산
- k :
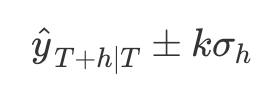
- 각각의 덧셈 상태 공간 모델에 대한 예측 분산 식
- sigma^2 : 잔차 분산
- m : 계절성 주기
- k : (h-1)/m의 정수 부분(시간 T+h 앞 예측 기간에서 연도의 개수)
