고차원 데이터
고차원 데이터란 X 변수의 수가 많은 데이터를 말한다. 이는 변수의 수가 많기 때문에 불필요한 변수가 존재하며 시각적으로 표현하기 어렵다. 또한 계산 복잡도가 증가하기 때문에 모델링이 비효율적일 가능성이 크다. 따라서 이 경우 중요한 변수만을 선택해서 모델링을 하는 것이 필요하며, 이를 차원 축소(dimension reduction)라고 한다.
변수 선택/추출을 통한 차원 축소
차원 축소의 방법은 변수 선택(feature selection)과 변수 추출(feature extraction) 두 가지가 있다. 변수 선택이란 분석 목적에 부합하는 소수의 예측 변수만을 선택하는 방법으로 본 데이터에서 변수를 선택하기 때문에 선택한 변수의 해석이 용이하지만 변수간 상관관계를 고려하기 어렵다는 단점이 있다. 변수 추출은 예측 변수의 변환을 통해 새로운 변수를 추출하는 방법으로 변수간 상관관계를 고려할 수 있고, 변수의 개수를 일반적으로 많이 줄일 수 있지만 추출된 변수의 해석이 어렵다는 단점이 있다. 변수 선택과 변수 추출은 지도 학습과 비지도 학습에 따라 다음과 같이 구분된다.
- Supervised feature selection :
Information gain,Stepwise regression,LASSO,Genetic algorithm - Supervised feature extraction :
Partial Least Squares(PLS) - Unsupervised feature selection :
PCA loading - Unsupervised feature extraction :
Principal Component Analysis(PCA),Wavelets transforms,Autoencoder
주성분 분석(Principal Components Analysis, PCA)
주성분 분석(PCA)는 고차원 데이터를 효과적으로 분석하기 위한 대표적 분석 기법으로 차원 축소, 시각화, 군집화, 압축 등이 가능하다. PCA는 n개의 관측치와 p개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터(n개의 관측치)로 요약하는 방식으로, 이 때 요약된 변수는 기존 변수의 선형 조합으로 생성된다. 즉, 원래 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 사영(projection)시키는 기법이다. PCA의 주요 목적은 데이터의 차원을 축소(n x p → n x k)하고, 데이터 시각화 및 해석에 있다. 일반적으로 PCA는 전체 분석 과정 중 초기에 사용한다.
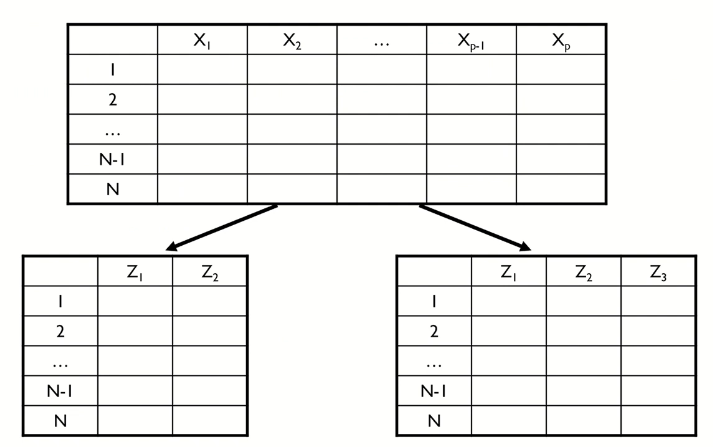
여기서 Z는 주성분이라고 하며, p개의 모든 원래 변수(original variable) X의 선형 결합(linear combination)이며, 이론 상으로 p개까지 생성될 수 있다.
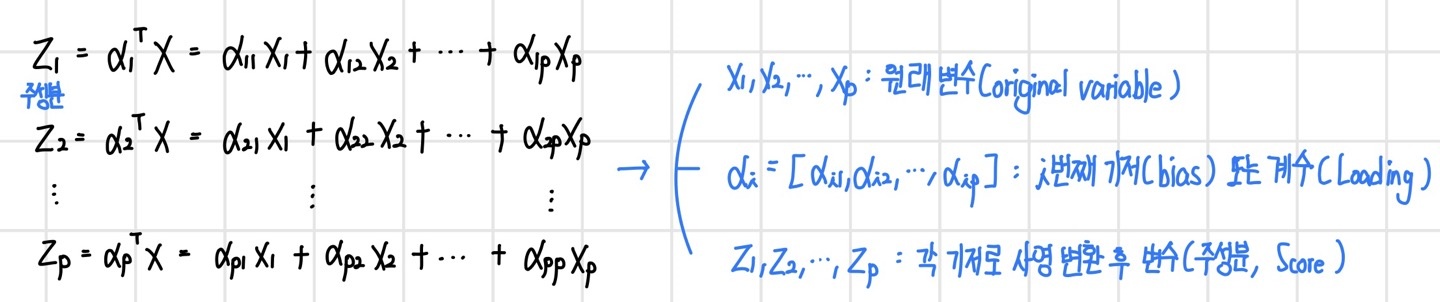
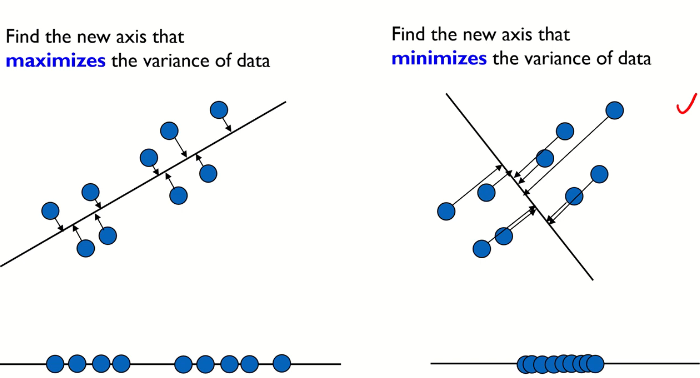
주성분 분석은 원 데이터의 분산을 최대화하는 축을 더 선호한다. 이를 그림으로 나타내면 다음과 같다. 왼쪽과 오른쪽 축이 있을 때, 주성분 분석의 관점에선 원 데이터를 사영시켰을 때 분산이 더 큰 왼쪽 축을 더 선호한다.
PCA 수리적 배경
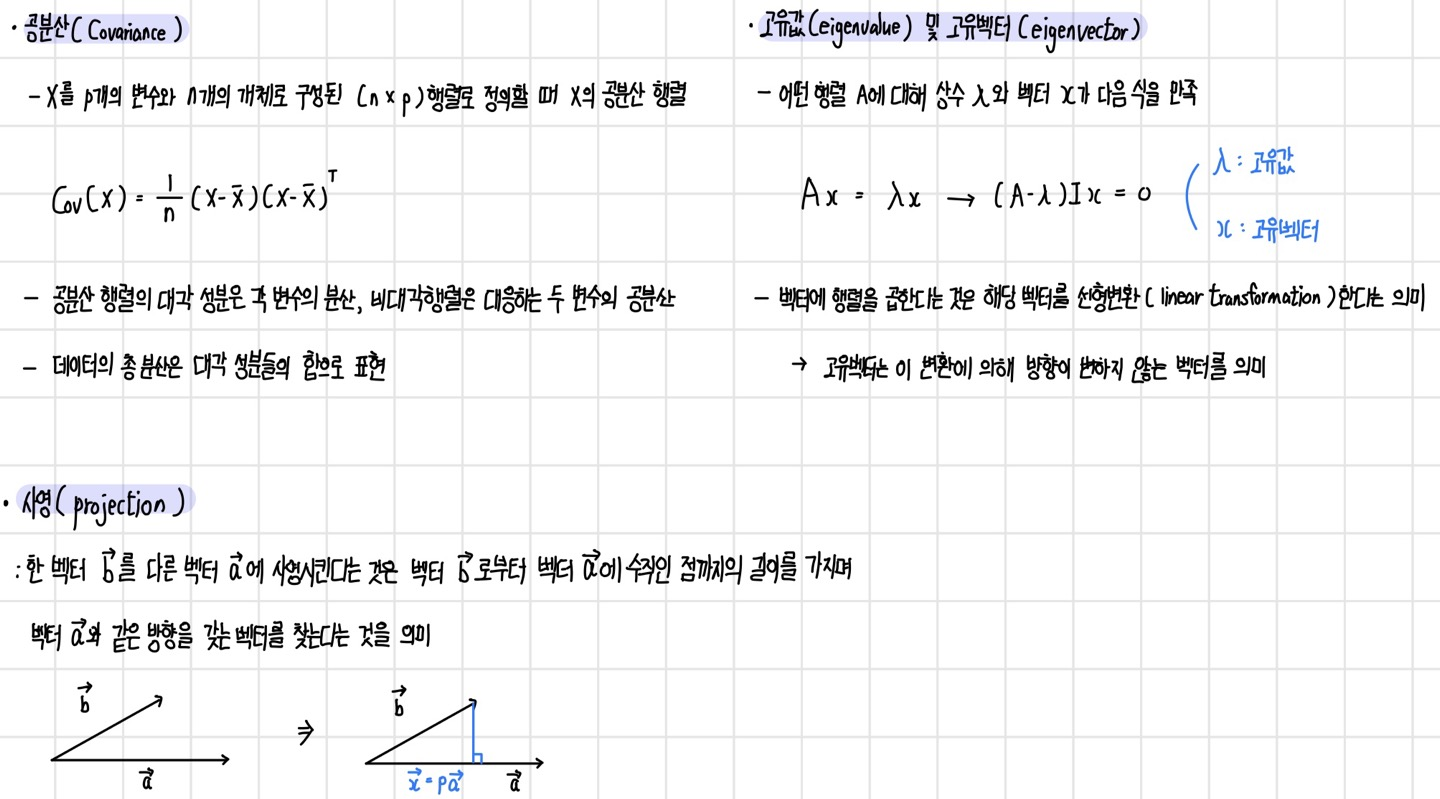
다음과 같이 X가 p개가 있는 다변량 데이터를 요약하는 방법에는 Mean vector, Covariance matrix, Correlation matrix 등이 있다. covariance matrix의 대각원소에는 p개의 변수에 대한 분산이 포함되어 있으며 비대각원소에는 2개 변수(fair)의 공분산이 포함되어 있다. correlation matrix의 경우에는 대각원소는 항상 1, 비대각원소는 2개 변수의 상관 계수가 포함되어 있다.

PCA의 수리적 배경에는 공분산(covariance), 사영(projection), 고유값(eigenvalue), 고유벡터(eigenvector) 등이 있다.
PCA 알고리즘 - 주성분 추출
PCA의 주 목적은 결국 Z의 분산을 가장 크게 하는 alpha 계수 값을 찾는 것이다. 이를 최적화 문제로 나타내면 다음과 같다. 참고로 데이터 X는 모든 X의 평균이 0이 되는 centered data이다.
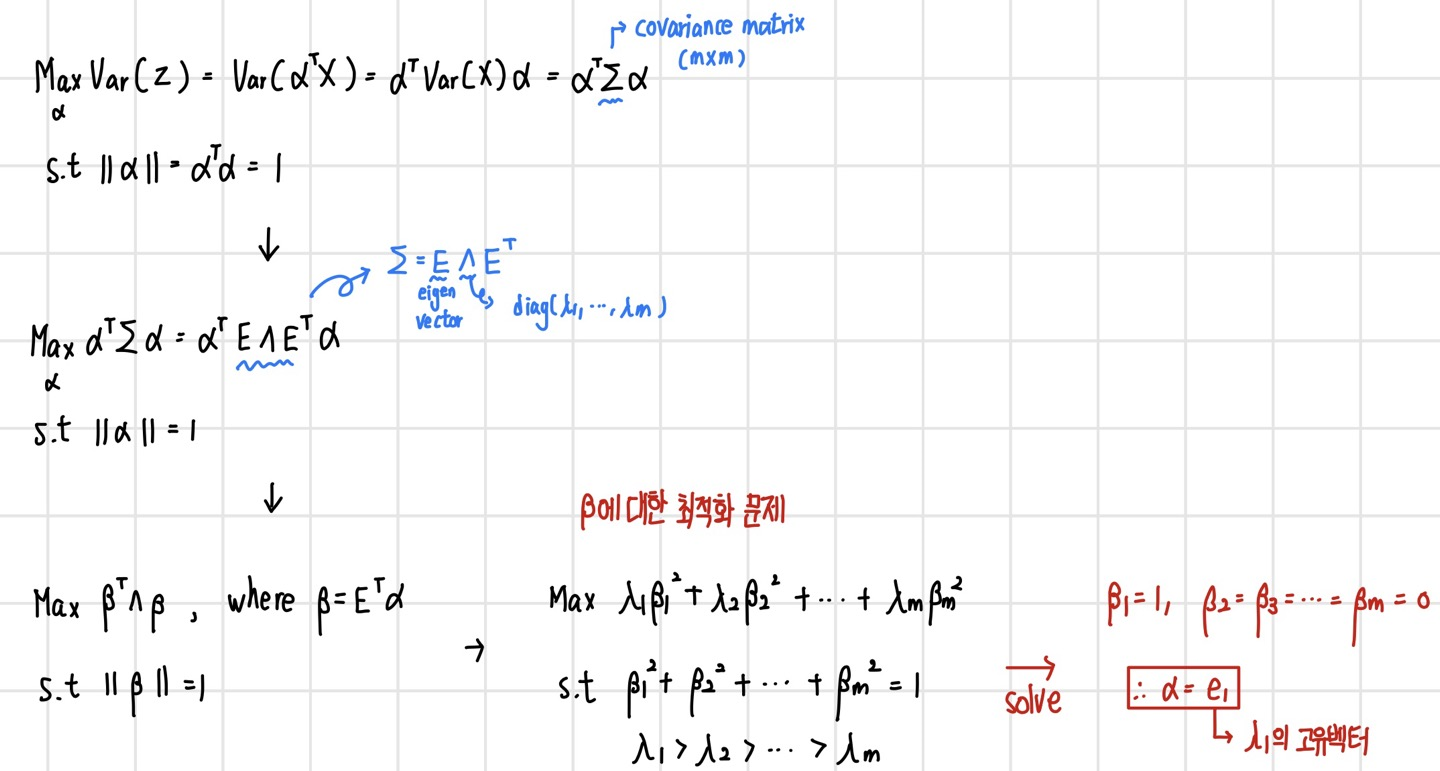
PCA - 예제
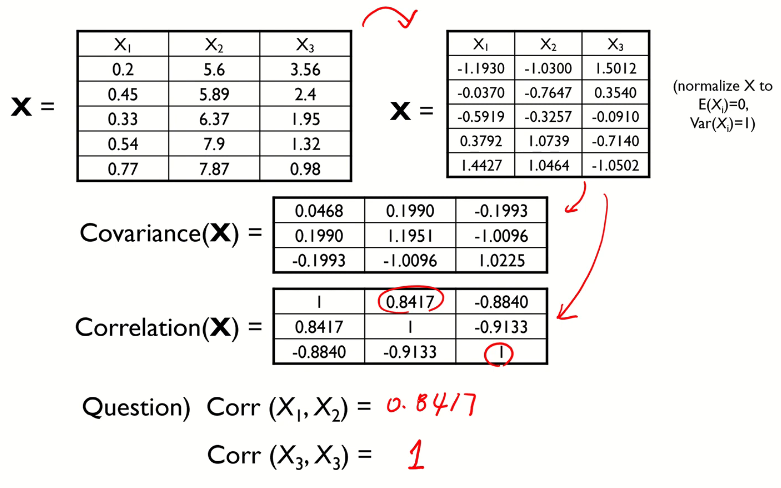
다음과 같이 변수가 3개인 데이터가 있다고 하자. 이 데이터에 대해 normalize(평균이 0, 분산이 1)를 진행하고 Covariance matrix와 Correlatin matrix를 계산했다.
이후 고유값과 고유 벡터를 계산하면 다음과 같다. 고유값은 숫자의 형태, 고유벡터는 벡터의 형태로 나타난다.

이후, 크기가 가장큰 lambda_3, lambda_2, lambda_1의 순으로 고유벡터와 X1, X2, X3를 곱해 Z1, Z2, Z3를 계산하고 최종적으로 주성분 분석으로 추출한 Z를 계산한다. 여기서 주성분의 성질은, 각각의 분산은 존재하지만 주성분 간에 공분산은 모두 0이라는 점이다. 즉, 주성분 Z1, Z2, Z3는 각각 독립이다.

이제 차원 축소를 위해 몇 개의 주성분을 사용하는가를 정해야 한다. 여기서 한가지 알아야할 점은, 원 데이터의 공분산 행렬의 고유값 lambda1, lambda2, lambda3는 주성분 Z1, Z2, Z3의 분산이라는 점이다. 따라서 전체 분산에 대한 각 주성분의 분산의 비율을 계산하면, 이는 해당 주성분이 전체 데이터의 몇 %를 표현하는지를 나타낼 수 있다.

이제 몇 개의 주성분을 선택할 것인지에 대해서는 두 가지의 방법이 있다.
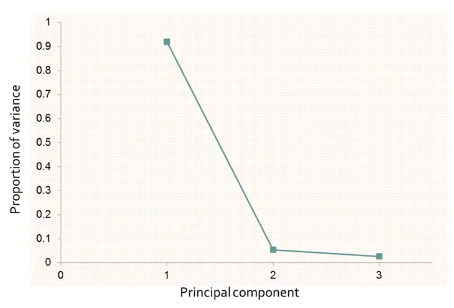
- 고유값 감소율이 유의미하게 낮아지는
Elbow Point에 해당하는 주성분 수를 선택 - 일정 수준 이상의 분산비를 보존하는 최소의 주성분을 선택(ex> 70%)
PCA Loading이란, 실제 변수가 주성분 결정에 얼마나 많은 영향을 주었는지 확인하는 것을 말한다. 앞서 계산한 주성분의 식에서 각 변수들의 계수값들의 크기를 시각화하여 계수 값이 큰 경우 많은 영향을 주었다고 판단한다.
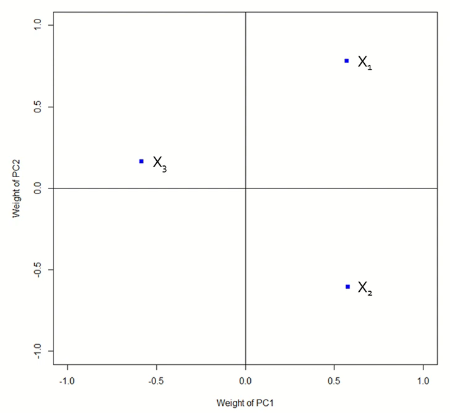
- X1 값이 증가하면 PC1(Z1)과 PC2(Z2)에 사영되는 값이 커지므로 중요한 변수일 가능성이 크다.
- X2 값이 증가하면 PC1 값은 증가하지만 PC2 값은 대량으로 감소한다.
- X3 값이 증가하면 PC1 값은 감소하며 PC2 값은 소폭으로 증가한다.
PCA 알고리즘 요약
- 데이터 정규화(Mean Centering)
- 기존 변수의 Covariance(Correlation) matrix 계산 → Mean Centering을 수행할 경우 Covariance와 Correlation matrix는 동일하지만, mean centering을 수행하지 않을 경우 값이 달라져 correlation matrix를 사용하는 것이 좋다.
- Covariance(Correlation) matrix로부터 Eigenvalue 및 이에 해당되는 Eigenvector를 계산
- Eigenvalue 및 해당되는 Eigenvectors를 순서대로 나열
- 정렬된 Eigenvector를 토대로 기존 변수를 변환
- 주성분 수를 결정하여 차원 축소 시행
PCA 한계
PCA는 공분산 행렬의 고유벡터를 사용하기 때문에 단일 가우시안(unimodal) 분포로 추정할 수 있는 데이터에 대해 서로 독립적인 축을 찾는데 사용할 수 있다. 그러나 데이터의 분포가 가우시안이 아니거나 다중 가우시안(multimodal) 자료들에 대해서는 적용하기가 어렵다. 이에 대한 대안으로 커널 PCA, LLE(Locally Linear Embedding) 등이 있다. 두 번째 한계점은 분류 및 예측 문제에 대해서 데이터의 범주 정보를 고려하지 않기 때문에 범주간 구분이 잘되도록 변환을 해주는 것은 아니라는 점이다. 이에 대한 대안으로는 Partial Least Square(PLS)가 있다.
이 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 수강하고 작성한 글입니다.
(이미지 출처 - 핵심 머신러닝)
고차원 데이터
고차원 데이터란 X 변수의 수가 많은 데이터를 말한다. 이는 변수의 수가 많기 때문에 불필요한 변수가 존재하며 시각적으로 표현하기 어렵다. 또한 계산 복잡도가 증가하기 때문에 모델링이 비효율적일 가능성이 크다. 따라서 이 경우 중요한 변수만을 선택해서 모델링을 하는 것이 필요하며, 이를 차원 축소(dimension reduction)라고 한다.
변수 선택/추출을 통한 차원 축소
차원 축소의 방법은 변수 선택(feature selection)과 변수 추출(feature extraction) 두 가지가 있다. 변수 선택이란 분석 목적에 부합하는 소수의 예측 변수만을 선택하는 방법으로 본 데이터에서 변수를 선택하기 때문에 선택한 변수의 해석이 용이하지만 변수간 상관관계를 고려하기 어렵다는 단점이 있다. 변수 추출은 예측 변수의 변환을 통해 새로운 변수를 추출하는 방법으로 변수간 상관관계를 고려할 수 있고, 변수의 개수를 일반적으로 많이 줄일 수 있지만 추출된 변수의 해석이 어렵다는 단점이 있다. 변수 선택과 변수 추출은 지도 학습과 비지도 학습에 따라 다음과 같이 구분된다.
- Supervised feature selection :
Information gain,Stepwise regression,LASSO,Genetic algorithm - Supervised feature extraction :
Partial Least Squares(PLS) - Unsupervised feature selection :
PCA loading - Unsupervised feature extraction :
Principal Component Analysis(PCA),Wavelets transforms,Autoencoder
주성분 분석(Principal Components Analysis, PCA)
주성분 분석(PCA)는 고차원 데이터를 효과적으로 분석하기 위한 대표적 분석 기법으로 차원 축소, 시각화, 군집화, 압축 등이 가능하다. PCA는 n개의 관측치와 p개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터(n개의 관측치)로 요약하는 방식으로, 이 때 요약된 변수는 기존 변수의 선형 조합으로 생성된다. 즉, 원래 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 사영(projection)시키는 기법이다. PCA의 주요 목적은 데이터의 차원을 축소(n x p → n x k)하고, 데이터 시각화 및 해석에 있다. 일반적으로 PCA는 전체 분석 과정 중 초기에 사용한다.

여기서 Z는 주성분이라고 하며, p개의 모든 원래 변수(original variable) X의 선형 결합(linear combination)이며, 이론 상으로 p개까지 생성될 수 있다.
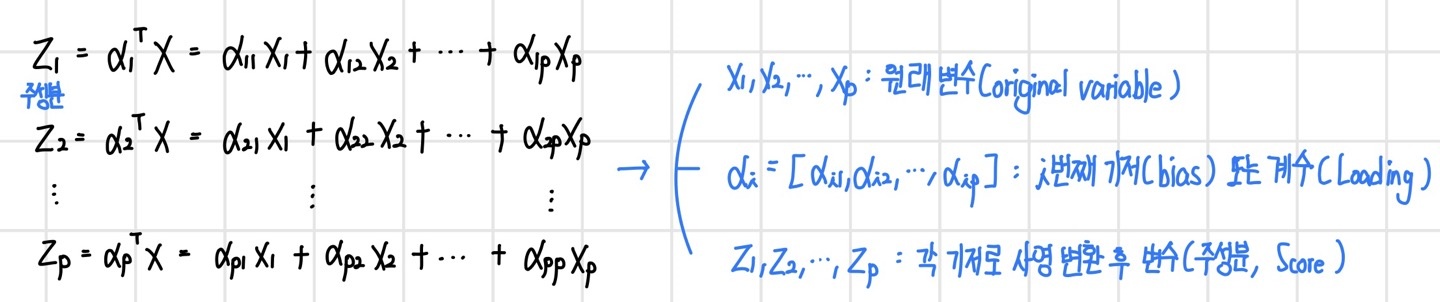
주성분 분석은 원 데이터의 분산을 최대화하는 축을 더 선호한다. 이를 그림으로 나타내면 다음과 같다. 왼쪽과 오른쪽 축이 있을 때, 주성분 분석의 관점에선 원 데이터를 사영시켰을 때 분산이 더 큰 왼쪽 축을 더 선호한다.

PCA 수리적 배경
다음과 같이 X가 p개가 있는 다변량 데이터를 요약하는 방법에는 Mean vector, Covariance matrix, Correlation matrix 등이 있다. covariance matrix의 대각원소에는 p개의 변수에 대한 분산이 포함되어 있으며 비대각원소에는 2개 변수(fair)의 공분산이 포함되어 있다. correlation matrix의 경우에는 대각원소는 항상 1, 비대각원소는 2개 변수의 상관 계수가 포함되어 있다.

PCA의 수리적 배경에는 공분산(covariance), 사영(projection), 고유값(eigenvalue), 고유벡터(eigenvector) 등이 있다.

PCA 알고리즘 - 주성분 추출
PCA의 주 목적은 결국 Z의 분산을 가장 크게 하는 alpha 계수 값을 찾는 것이다. 이를 최적화 문제로 나타내면 다음과 같다. 참고로 데이터 X는 모든 X의 평균이 0이 되는 centered data이다.
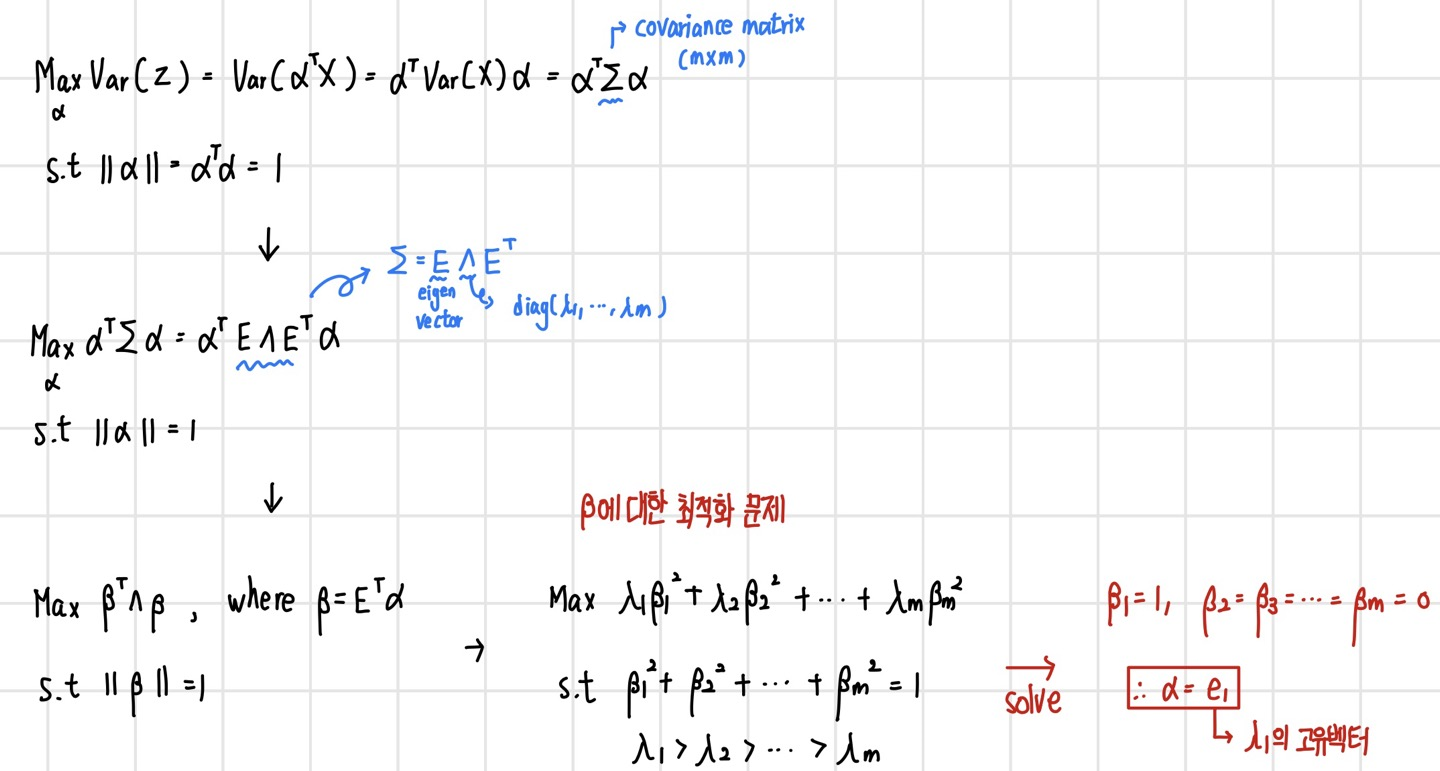
PCA - 예제
다음과 같이 변수가 3개인 데이터가 있다고 하자. 이 데이터에 대해 normalize(평균이 0, 분산이 1)를 진행하고 Covariance matrix와 Correlatin matrix를 계산했다.

이후 고유값과 고유 벡터를 계산하면 다음과 같다. 고유값은 숫자의 형태, 고유벡터는 벡터의 형태로 나타난다.

이후, 크기가 가장큰 lambda_3, lambda_2, lambda_1의 순으로 고유벡터와 X1, X2, X3를 곱해 Z1, Z2, Z3를 계산하고 최종적으로 주성분 분석으로 추출한 Z를 계산한다. 여기서 주성분의 성질은, 각각의 분산은 존재하지만 주성분 간에 공분산은 모두 0이라는 점이다. 즉, 주성분 Z1, Z2, Z3는 각각 독립이다.

이제 차원 축소를 위해 몇 개의 주성분을 사용하는가를 정해야 한다. 여기서 한가지 알아야할 점은, 원 데이터의 공분산 행렬의 고유값 lambda1, lambda2, lambda3는 주성분 Z1, Z2, Z3의 분산이라는 점이다. 따라서 전체 분산에 대한 각 주성분의 분산의 비율을 계산하면, 이는 해당 주성분이 전체 데이터의 몇 %를 표현하는지를 나타낼 수 있다.

이제 몇 개의 주성분을 선택할 것인지에 대해서는 두 가지의 방법이 있다.

- 고유값 감소율이 유의미하게 낮아지는
Elbow Point에 해당하는 주성분 수를 선택 - 일정 수준 이상의 분산비를 보존하는 최소의 주성분을 선택(ex> 70%)
PCA Loading이란, 실제 변수가 주성분 결정에 얼마나 많은 영향을 주었는지 확인하는 것을 말한다. 앞서 계산한 주성분의 식에서 각 변수들의 계수값들의 크기를 시각화하여 계수 값이 큰 경우 많은 영향을 주었다고 판단한다.

- X1 값이 증가하면 PC1(Z1)과 PC2(Z2)에 사영되는 값이 커지므로 중요한 변수일 가능성이 크다.
- X2 값이 증가하면 PC1 값은 증가하지만 PC2 값은 대량으로 감소한다.
- X3 값이 증가하면 PC1 값은 감소하며 PC2 값은 소폭으로 증가한다.
PCA 알고리즘 요약
- 데이터 정규화(Mean Centering)
- 기존 변수의 Covariance(Correlation) matrix 계산 → Mean Centering을 수행할 경우 Covariance와 Correlation matrix는 동일하지만, mean centering을 수행하지 않을 경우 값이 달라져 correlation matrix를 사용하는 것이 좋다.
- Covariance(Correlation) matrix로부터 Eigenvalue 및 이에 해당되는 Eigenvector를 계산
- Eigenvalue 및 해당되는 Eigenvectors를 순서대로 나열
- 정렬된 Eigenvector를 토대로 기존 변수를 변환
- 주성분 수를 결정하여 차원 축소 시행
PCA 한계
PCA는 공분산 행렬의 고유벡터를 사용하기 때문에 단일 가우시안(unimodal) 분포로 추정할 수 있는 데이터에 대해 서로 독립적인 축을 찾는데 사용할 수 있다. 그러나 데이터의 분포가 가우시안이 아니거나 다중 가우시안(multimodal) 자료들에 대해서는 적용하기가 어렵다. 이에 대한 대안으로 커널 PCA, LLE(Locally Linear Embedding) 등이 있다. 두 번째 한계점은 분류 및 예측 문제에 대해서 데이터의 범주 정보를 고려하지 않기 때문에 범주간 구분이 잘되도록 변환을 해주는 것은 아니라는 점이다. 이에 대한 대안으로는 Partial Least Square(PLS)가 있다.
이 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 수강하고 작성한 글입니다.
(이미지 출처 - 핵심 머신러닝)