Good Model
좋은 모델이란 두 가지로 나눌 수 있다. 첫 번째는 현재 데이터(training data)를 잘 설명하는 모델(Explanatory modeling)이며, 두 번째는 미래 데이터(testing data)에 대한 예측 성능이 좋은 모델(Predictive modeling)이다. 좋은 Explanatory model이란 training error를 minimize하는 모델이다. 타깃 값이 연속형일 경우 MSE 값을 minimize 하는 경우이다. 또한 좋은 Predictive Model이란 미래 데이터에 대한 expected error가 낮은 모델이다. 이 경우에는 Expected MSE값을 감소시켜야 한다.
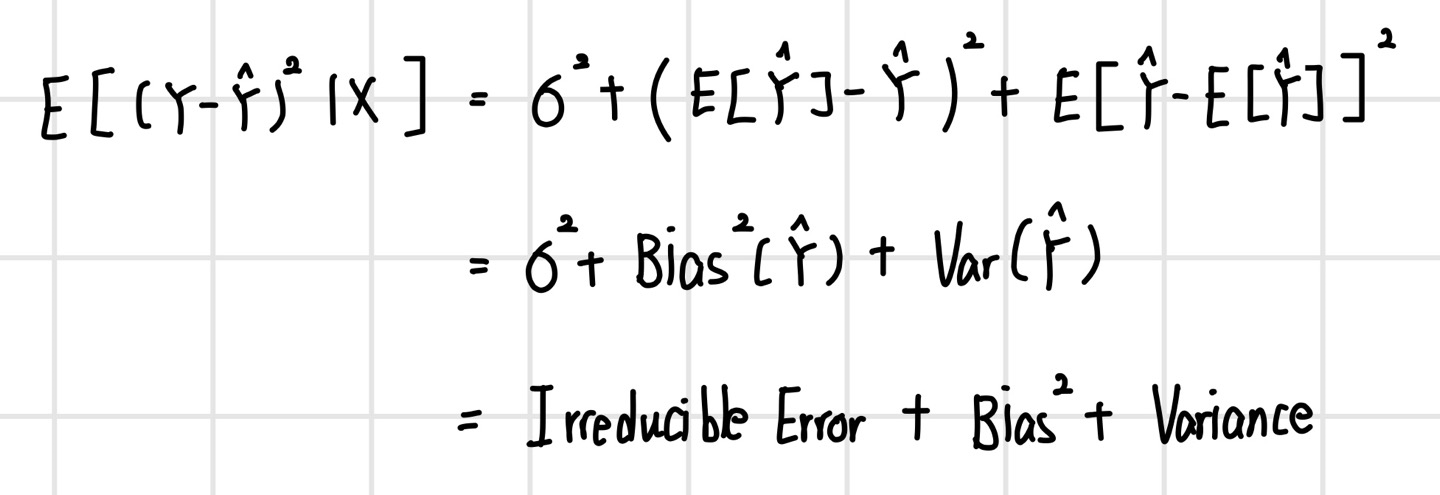
여기서 Irreducible Error는 어떻게 할 방법이 없는 오류를 말하며, Expected MSE를 줄이기 위해선 Bias와 Variance, 혹은 둘 다 낮춰야 한다. 만약 그렇지 못하더라도 둘 중에 하나라도 작으면 좋은 경우이다. 또한 Bias가 증가되더라도 Variance 감소폭이 더 크다면 Expected MSE는 감소하여 예측 성능이 증가한다.
Subset Selection
Least squares method(최소제곱법)을 통해 계산한 평균제곱오차(MSE)를 최소화하는 회귀계수 beta에 대한 unbiased estimator 중 가장 분산이 작은 estimator를 Best Linear Unbiased Estimator, BLUE라고 했다. 또한 이는 Gauss-Markov Theorem을 통해 증명되었다. 하지만 여기에 더해 bias는 어느 정도 감안하더라도 분산을 낮추는 방법도 있다. 이것이 바로 Subset selection method이다. Subset selection이란 전체 p개의 설명 변수(X) 중 일부 k개만을 사용하여 회귀 계수 beta를 추정하는 방법이다. 이는 전체 변수 중 일부만을 선택함에 따라 bias는 증가할 수 있지만 variance가 감소하는 효과가 있다. 이러한 Subset Selection 방법은 여러가지가 있다.
- Best subset selection
- Forward stepwise selection
- Backward stepwise selection
- Least angle regression
- Orthogonal matching pursuit
Regularization Concept

해당 식에서 람다(lambda)는 서로 상충하는 training accuracy와 Generalization accuracy를 컨트롤하는 하이퍼파라미터이다. 만약 이 값이 매우 크다면 절편을 제외한 모든 파라미터 값들이 Loss를 최소화하기 위해서 0에 가까워진다. 이 경우 Underfitting되었다고 한다. 반대로 람다 값이 매우 작아지면 제약에 대한 효과가 거의 없어지기 때문에 파라미터들이 모두 살아있게 되고, bias는 작아지지만 variance가 매우 커 Overfitting이 발생한다.
Regularization Method
정규화(Regularization)는 회귀 계수 beta가 가질 수 있는 값에 제약조건을 부여하는 방법이다. 이러한 제약 조건에 의해 bias가 증가할 수 있지만, variance가 감소하게 된다.
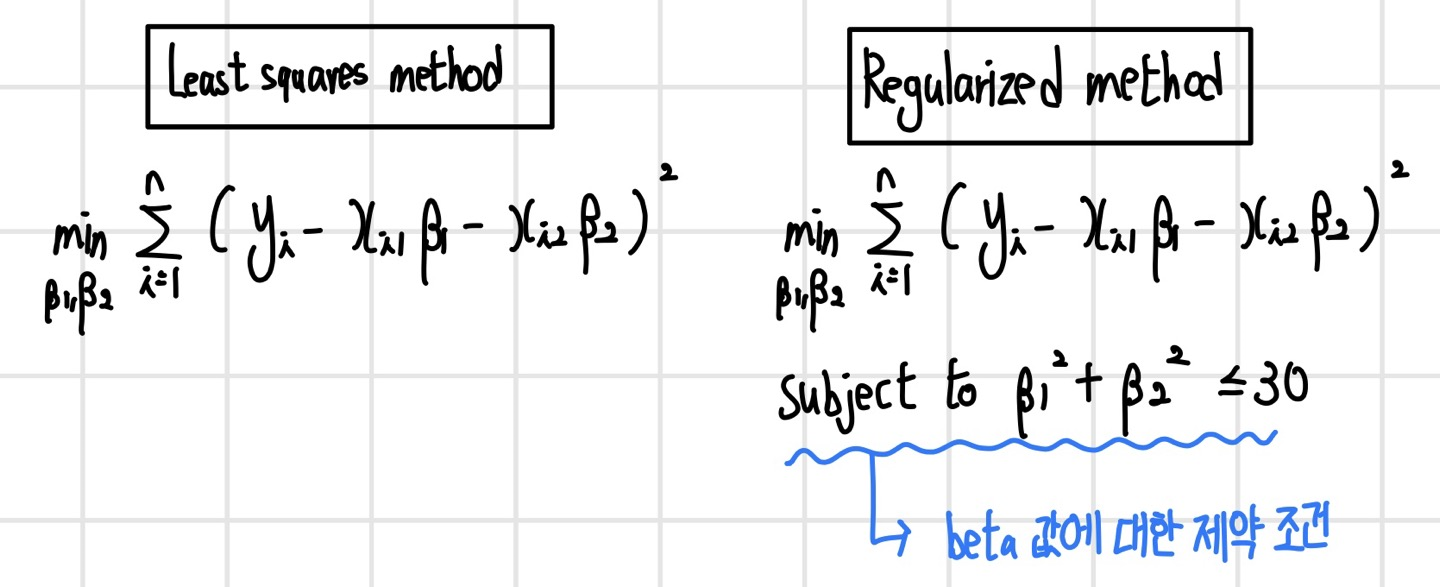
Ridge Regression
Ridge Regression은 제곱 오차를 최소화하면서 회귀 계수의 L2-norm을 제한한다.

MSE(beta1, beta2)를 좀 더 자세히 보면 다음과 같다.
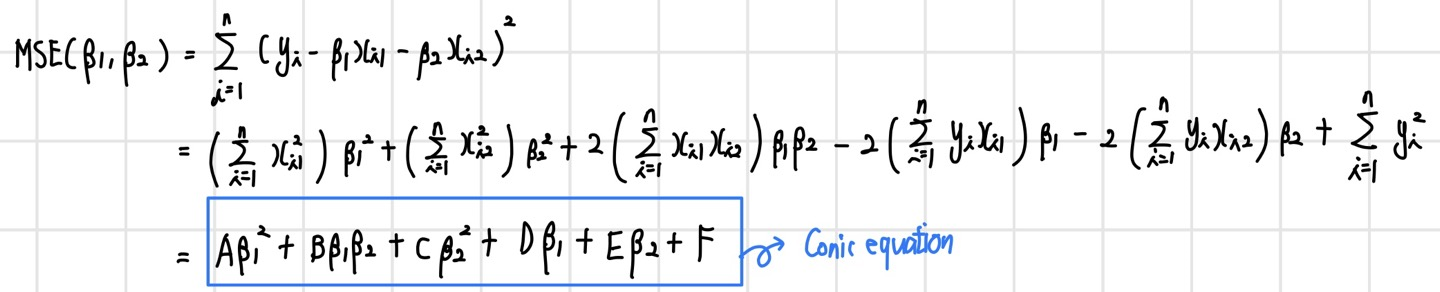
이 Conic equation의 판별식은 B^2 - 4AC인데, 이를 계산해보면 0보다 작은 값이 나온다. 이는 곧 실제 y값과 선형식을 통해 나온 y값의 차이의 제곱을 나타내는 MSE는 타원의 모양이라는 것을 알 수 있다. 이렇게 제약 조건을 만족하며 에러를 최소화하는 beta 값을 찾는 과정은 다음과 같다. 이 경우 beta 값들은 LS보다 작아진다(shrinkage).
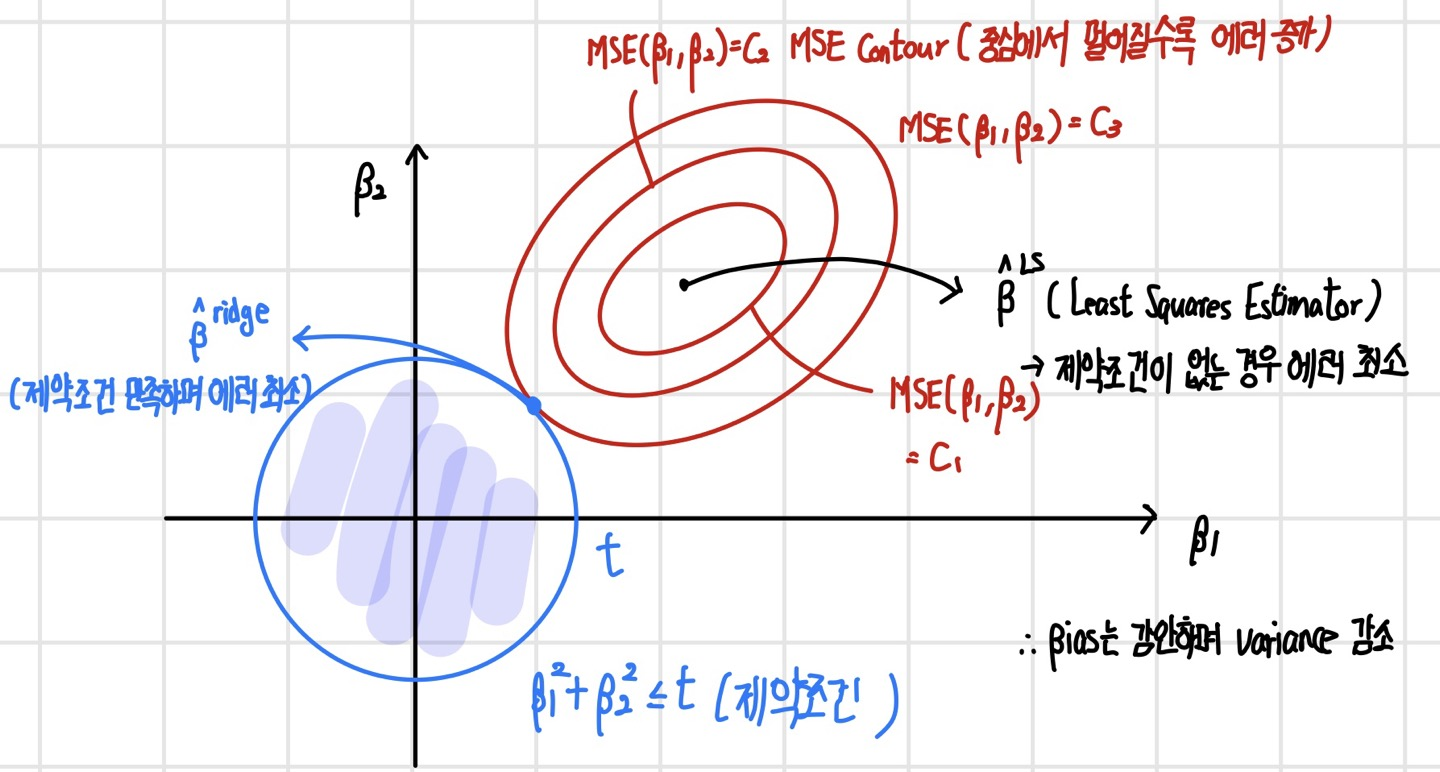
회귀계수 파라미터 값(beta)은 tuning parameter t에 의하여 다음과 같이 변화한다. t값이 작아지면 작아질수록 회귀계수 파라미터 값은 줄어들어 0에 수렴하게 된다.
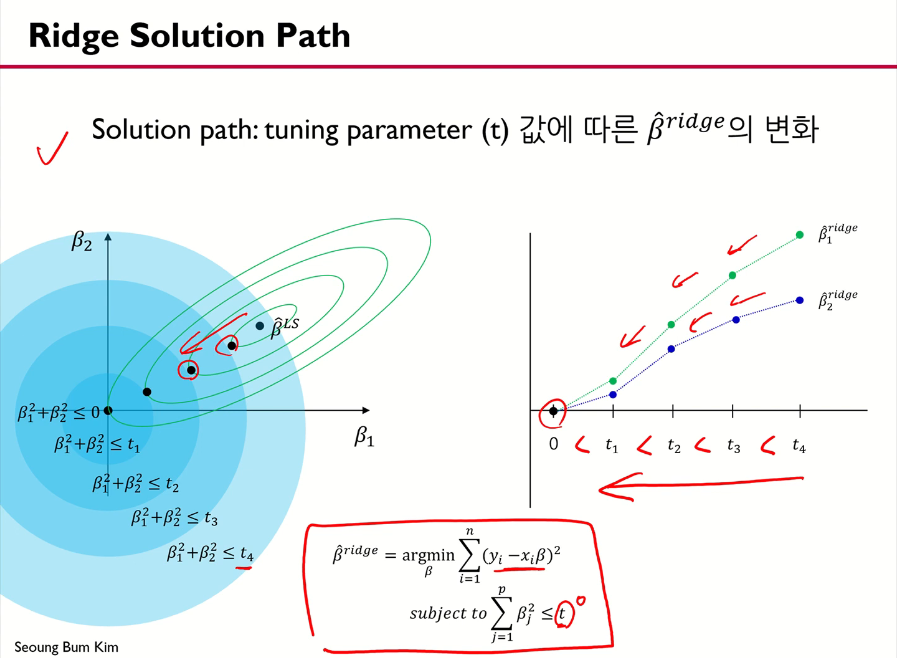
Ridge는 행렬 연산을 통해 closed form solution을 구할 수 있다. 결론적으로 계산된 beta(ridge)는 beta(LS)보다 variance가 작은데, 이는 training data에 대한 설명은 부족하지만 예측 면에서 유리하다.

Lasso Regression
LASSO(Least Absolute Shrinkage and Selection Operator) 회귀 모델은 앞서 Ridge 모델에서 확인한 shrinkage, 즉 회귀 계수 파라미터들의 값이 작아지는 것과 더불어 Y를 예측하는데 중요한 X 변수를 자동으로 선택하는 기능까지 있는 모델이다. Lasso 모델은 Ridge와 유사하지만 제약식에서 차이가 있다. Lasso는 회귀 계수 파라미터의 L1-norm, 즉 절댓값의 합에 대한 제약식으로 구성된다. 해당 식에서 t 값이 작아지면 제약이 매우 강해지는 것을 의미하며, 이는 람다 값은 높아졌을 때 같은 의미이다. 반대로 t 값이 커지면 제약이 거의 없어진다는 것을 의미하며, 이는 람다 값은 낮아졌을 때와 같은 의미이다.

Lasso Regression의 solution path는 다음과 같다. Ridge 모델과는 다르게 Lasso 모델은 제약식이 절댓값과 관련되어 있어 원이 아닌 마름모가 나타나게 된다. 여기서 제약 조건을 만족하며 에러를 최소화하는 지점은 항상 마름모의 꼭짓점인데, 이 경우 일부 파라미터의 값이 0이 될 수 있어 변수 선택이 가능해진다. 또한 Ridge 모델과 동일하게 shrinkage 또한 발생하는 것을 확인할 수 있다.
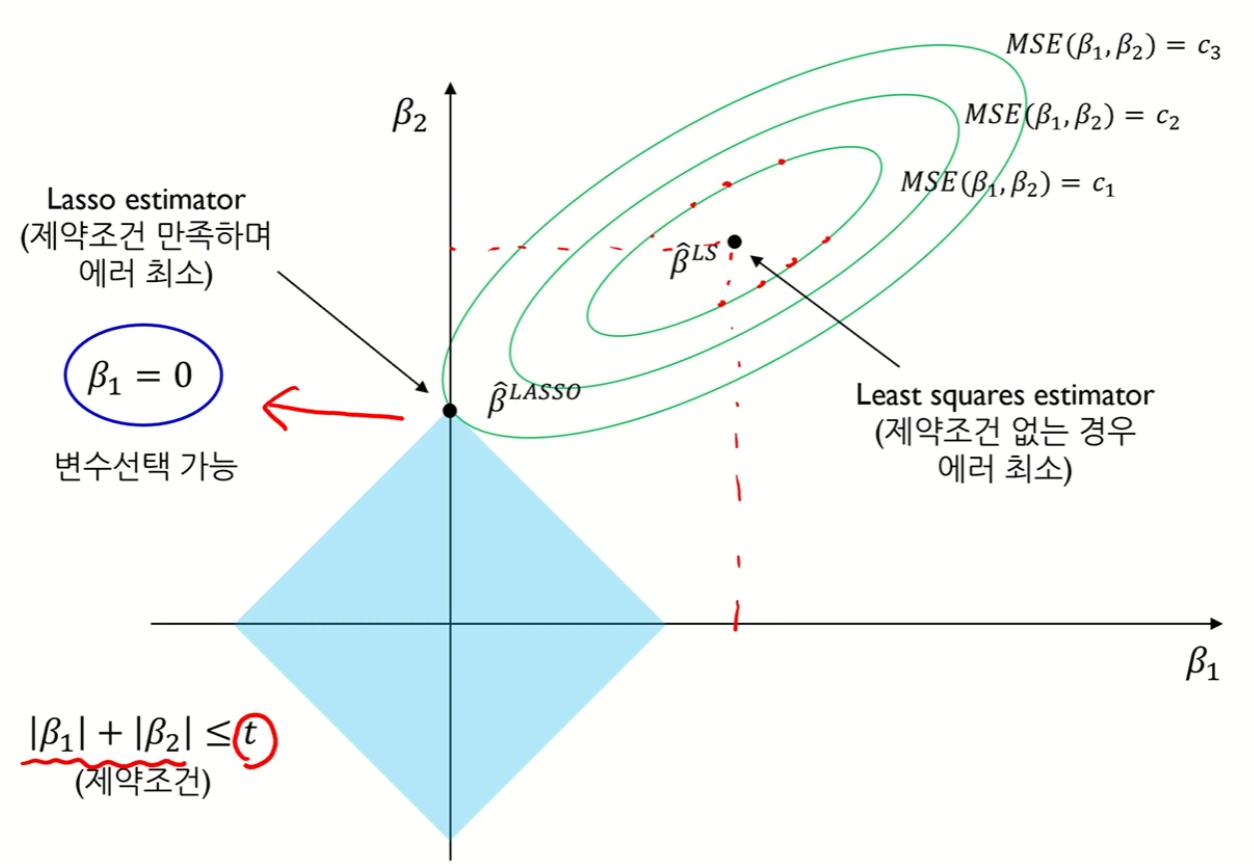
Lasso formulation은 Ridge와 달리 L1-norm이 미분이 불가능하기 때문에 closed form solution을 구하는 것이 불가능하다. 따라서 수치 최적화 기법을 사용하는데, 이러한 수치 최적화 기법에는 Quadratic programming techniques, LARS algorithm, Coordinate descent algorithm 등이 있다.
Lasso Parameter
Lasso Regression의 식에서 람다는 사용자가 설정하는 하이퍼 파라미터 값이다. 이 람다 값을 0으로 설정할 경우 제약식이 없어지기 때문에 Least Square와 동일해진다. 반대로 람다 값을 무한히 크게 설정하면, 회귀 계수 파라미터들에 매우 강한 제약을 하는 것이기 때문에 대부분의 파라미터 값들이 0이 되어 constant한 값이 나오게 된다. 여기서 람다의 값을 어떻게 설정하는가는 결국 몇 개의 변수를 선택하는가에 대한 문제와 동일하다. 여기서 만약 람다 값을 크게 설정할 경우, 일부 변수만 선택되기 때문에 적은 변수를 사용하고 간단한 모델이 되어 해석하기 쉽지만 높은 학습 오차로 인해 underfitting의 위험성이 커진다. 반대로 람다 값을 작게 설정할 경우 많은 변수가 선택되어 복잡한 모델이 되어 해석하기 어렵지만 낮은 학습 오차로 인해 overfitting의 위험성이 커진다. 따라서 람다 값은 적절한 절충안을 찾는 것이 중요하다. 추가적으로, Lasso는 데이터의 변화에 대해 비교적 강건한(robust) 모델로, 회귀 계수 파라미터들의 값들의 차이가 데이터가 변화함에 따라 크지 않다.
Solution Paths Ridge and Lasso
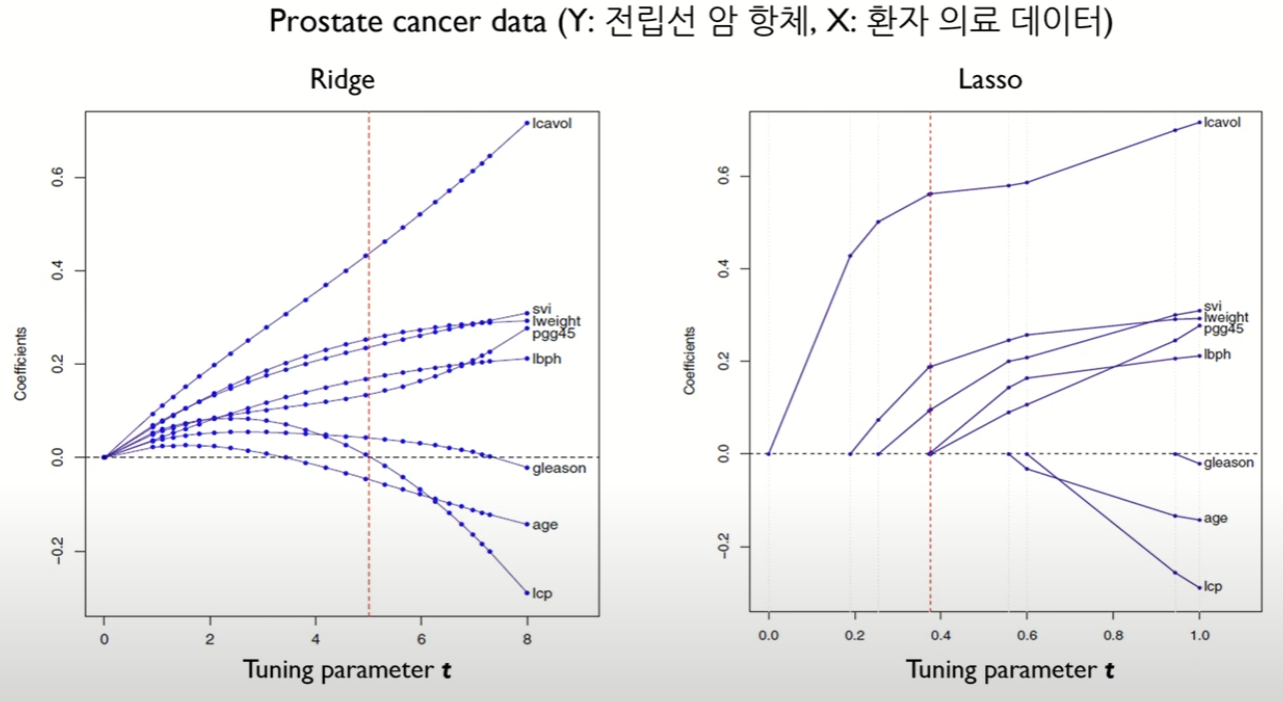
동일한 데이터(Prostate cancer data)에 대하여 Ridge와 Lasso의 Tuning parameter t에 대해 회귀 계수 파라미터 값들의 변화를 그래프로 나타내었다. 이를 통해 확인할 수 있는 점은 Ridge와 Lasso 모두 t가 작아짐에 따라 모든 계수의 크기가 감소한다는 점이다. 그러나 Ridge의 경우 이 회귀 계수 값들이 0이 되진 않지만, Lasso는 예측에 중요하지 않은 변수가 더 빠르게 감소하며 t가 작아짐에 따라 에측에 중요하지 않은 변수가 0이 되는 것을 확인할 수 있다.
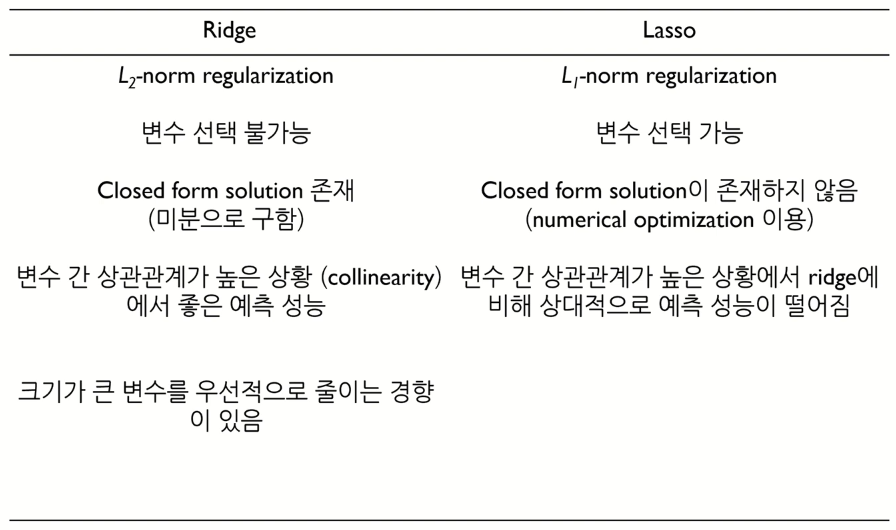
지금까지 확인한 Ridge와 Lasso를 비교하면 다음과 같다.
Lasso Limitation
Lasso의 한계점은, 변수들 간의 상관관계가 큰 경우 변수 선택과 예측의 성능이 저하된다는 것이다. 따라서 변수 간 상관관계를 반영할 수 있는 방법이 필요하다. 다음 그림을 확인해보면 변수 간의 상관관계가 높을 경우 boxplot의 box의 크기가 커져 회귀 계수들의 값의 차이가 커지는 것을 확인할 수 있다.
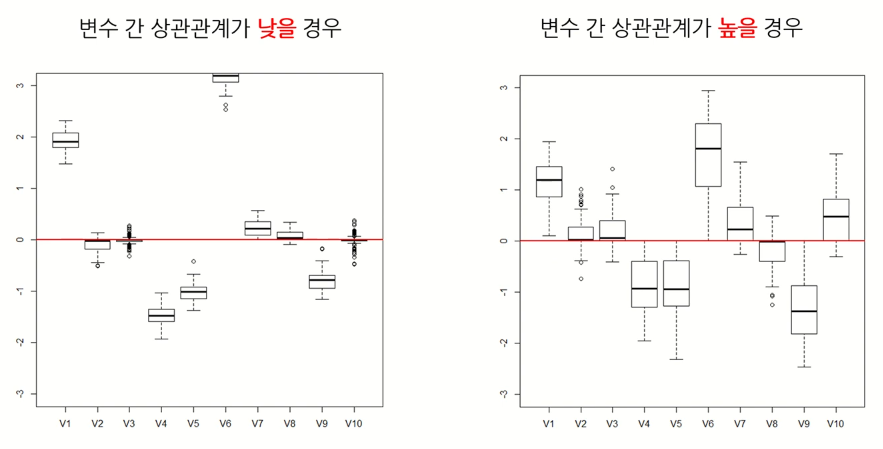
Elastic-Net
이러한 Lasso의 Limitation을 해결하기 위해 나온 모델이 Elastic Net이다. 이는 Ridge와 Lasso를 결합한 모델이다(L1- and L2-regularization). Elastic-Net은 상관관계가 큰 변수를 동시에 선택 혹은 배제하는 특성이 있다. Elastic-Net은 파라미터 람다1, 람다2를 선정하는 특별한 방법이 있진 않다. Grid Search를 통해 일정 범위 내로 두 파라미터를 조정하여 가장 좋은 예측 결과를 보이는 값을 선정하게 된다.

본 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 듣고 작성한 글입니다.
Good Model
좋은 모델이란 두 가지로 나눌 수 있다. 첫 번째는 현재 데이터(training data)를 잘 설명하는 모델(Explanatory modeling)이며, 두 번째는 미래 데이터(testing data)에 대한 예측 성능이 좋은 모델(Predictive modeling)이다. 좋은 Explanatory model이란 training error를 minimize하는 모델이다. 타깃 값이 연속형일 경우 MSE 값을 minimize 하는 경우이다. 또한 좋은 Predictive Model이란 미래 데이터에 대한 expected error가 낮은 모델이다. 이 경우에는 Expected MSE값을 감소시켜야 한다.
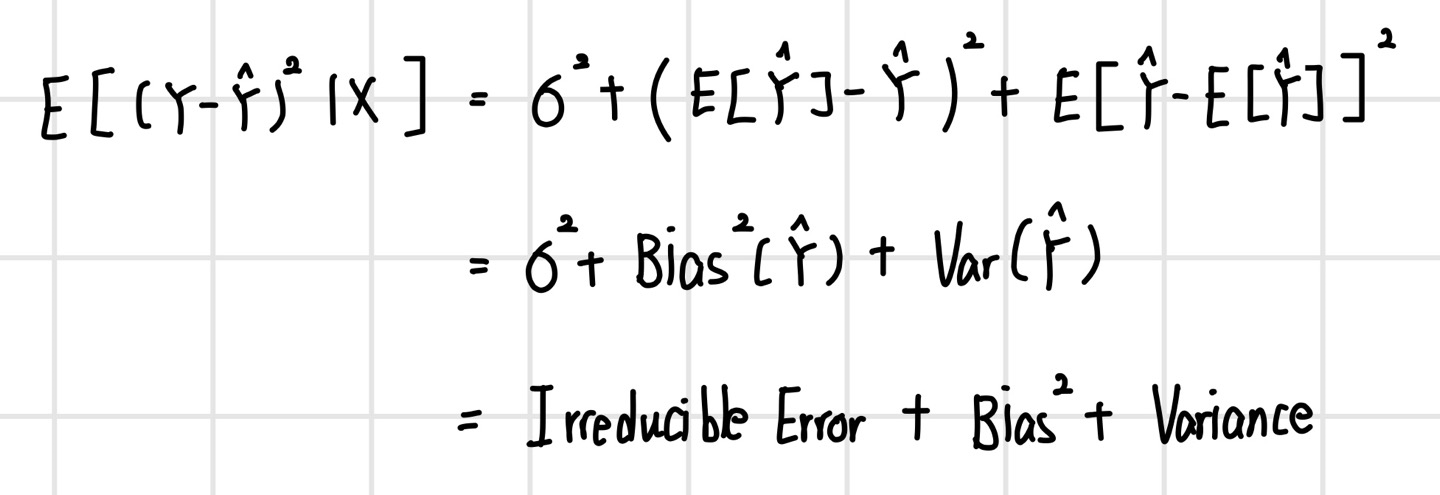
여기서 Irreducible Error는 어떻게 할 방법이 없는 오류를 말하며, Expected MSE를 줄이기 위해선 Bias와 Variance, 혹은 둘 다 낮춰야 한다. 만약 그렇지 못하더라도 둘 중에 하나라도 작으면 좋은 경우이다. 또한 Bias가 증가되더라도 Variance 감소폭이 더 크다면 Expected MSE는 감소하여 예측 성능이 증가한다.
Subset Selection
Least squares method(최소제곱법)을 통해 계산한 평균제곱오차(MSE)를 최소화하는 회귀계수 beta에 대한 unbiased estimator 중 가장 분산이 작은 estimator를 Best Linear Unbiased Estimator, BLUE라고 했다. 또한 이는 Gauss-Markov Theorem을 통해 증명되었다. 하지만 여기에 더해 bias는 어느 정도 감안하더라도 분산을 낮추는 방법도 있다. 이것이 바로 Subset selection method이다. Subset selection이란 전체 p개의 설명 변수(X) 중 일부 k개만을 사용하여 회귀 계수 beta를 추정하는 방법이다. 이는 전체 변수 중 일부만을 선택함에 따라 bias는 증가할 수 있지만 variance가 감소하는 효과가 있다. 이러한 Subset Selection 방법은 여러가지가 있다.
- Best subset selection
- Forward stepwise selection
- Backward stepwise selection
- Least angle regression
- Orthogonal matching pursuit
Regularization Concept

해당 식에서 람다(lambda)는 서로 상충하는 training accuracy와 Generalization accuracy를 컨트롤하는 하이퍼파라미터이다. 만약 이 값이 매우 크다면 절편을 제외한 모든 파라미터 값들이 Loss를 최소화하기 위해서 0에 가까워진다. 이 경우 Underfitting되었다고 한다. 반대로 람다 값이 매우 작아지면 제약에 대한 효과가 거의 없어지기 때문에 파라미터들이 모두 살아있게 되고, bias는 작아지지만 variance가 매우 커 Overfitting이 발생한다.
Regularization Method
정규화(Regularization)는 회귀 계수 beta가 가질 수 있는 값에 제약조건을 부여하는 방법이다. 이러한 제약 조건에 의해 bias가 증가할 수 있지만, variance가 감소하게 된다.

Ridge Regression
Ridge Regression은 제곱 오차를 최소화하면서 회귀 계수의 L2-norm을 제한한다.

MSE(beta1, beta2)를 좀 더 자세히 보면 다음과 같다.
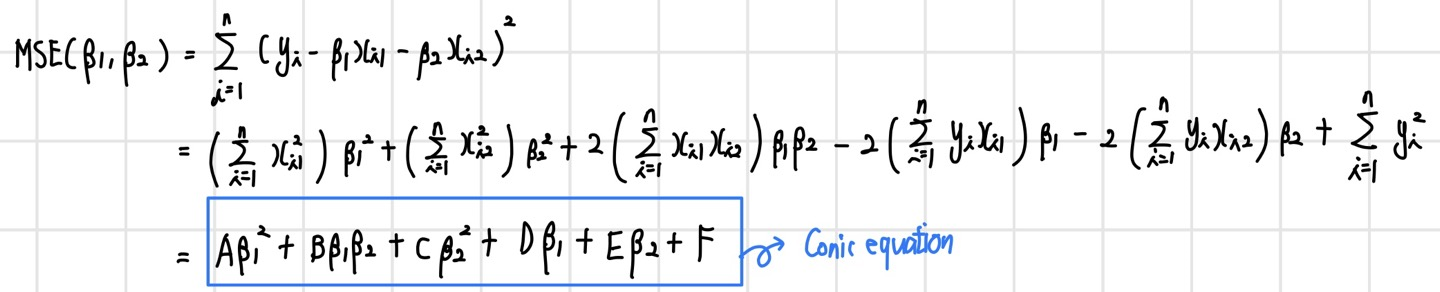
이 Conic equation의 판별식은 B^2 - 4AC인데, 이를 계산해보면 0보다 작은 값이 나온다. 이는 곧 실제 y값과 선형식을 통해 나온 y값의 차이의 제곱을 나타내는 MSE는 타원의 모양이라는 것을 알 수 있다. 이렇게 제약 조건을 만족하며 에러를 최소화하는 beta 값을 찾는 과정은 다음과 같다. 이 경우 beta 값들은 LS보다 작아진다(shrinkage).

회귀계수 파라미터 값(beta)은 tuning parameter t에 의하여 다음과 같이 변화한다. t값이 작아지면 작아질수록 회귀계수 파라미터 값은 줄어들어 0에 수렴하게 된다.

Ridge는 행렬 연산을 통해 closed form solution을 구할 수 있다. 결론적으로 계산된 beta(ridge)는 beta(LS)보다 variance가 작은데, 이는 training data에 대한 설명은 부족하지만 예측 면에서 유리하다.

Lasso Regression
LASSO(Least Absolute Shrinkage and Selection Operator) 회귀 모델은 앞서 Ridge 모델에서 확인한 shrinkage, 즉 회귀 계수 파라미터들의 값이 작아지는 것과 더불어 Y를 예측하는데 중요한 X 변수를 자동으로 선택하는 기능까지 있는 모델이다. Lasso 모델은 Ridge와 유사하지만 제약식에서 차이가 있다. Lasso는 회귀 계수 파라미터의 L1-norm, 즉 절댓값의 합에 대한 제약식으로 구성된다. 해당 식에서 t 값이 작아지면 제약이 매우 강해지는 것을 의미하며, 이는 람다 값은 높아졌을 때 같은 의미이다. 반대로 t 값이 커지면 제약이 거의 없어진다는 것을 의미하며, 이는 람다 값은 낮아졌을 때와 같은 의미이다.

Lasso Regression의 solution path는 다음과 같다. Ridge 모델과는 다르게 Lasso 모델은 제약식이 절댓값과 관련되어 있어 원이 아닌 마름모가 나타나게 된다. 여기서 제약 조건을 만족하며 에러를 최소화하는 지점은 항상 마름모의 꼭짓점인데, 이 경우 일부 파라미터의 값이 0이 될 수 있어 변수 선택이 가능해진다. 또한 Ridge 모델과 동일하게 shrinkage 또한 발생하는 것을 확인할 수 있다.

Lasso formulation은 Ridge와 달리 L1-norm이 미분이 불가능하기 때문에 closed form solution을 구하는 것이 불가능하다. 따라서 수치 최적화 기법을 사용하는데, 이러한 수치 최적화 기법에는 Quadratic programming techniques, LARS algorithm, Coordinate descent algorithm 등이 있다.
Lasso Parameter
Lasso Regression의 식에서 람다는 사용자가 설정하는 하이퍼 파라미터 값이다. 이 람다 값을 0으로 설정할 경우 제약식이 없어지기 때문에 Least Square와 동일해진다. 반대로 람다 값을 무한히 크게 설정하면, 회귀 계수 파라미터들에 매우 강한 제약을 하는 것이기 때문에 대부분의 파라미터 값들이 0이 되어 constant한 값이 나오게 된다. 여기서 람다의 값을 어떻게 설정하는가는 결국 몇 개의 변수를 선택하는가에 대한 문제와 동일하다. 여기서 만약 람다 값을 크게 설정할 경우, 일부 변수만 선택되기 때문에 적은 변수를 사용하고 간단한 모델이 되어 해석하기 쉽지만 높은 학습 오차로 인해 underfitting의 위험성이 커진다. 반대로 람다 값을 작게 설정할 경우 많은 변수가 선택되어 복잡한 모델이 되어 해석하기 어렵지만 낮은 학습 오차로 인해 overfitting의 위험성이 커진다. 따라서 람다 값은 적절한 절충안을 찾는 것이 중요하다. 추가적으로, Lasso는 데이터의 변화에 대해 비교적 강건한(robust) 모델로, 회귀 계수 파라미터들의 값들의 차이가 데이터가 변화함에 따라 크지 않다.
Solution Paths Ridge and Lasso
동일한 데이터(Prostate cancer data)에 대하여 Ridge와 Lasso의 Tuning parameter t에 대해 회귀 계수 파라미터 값들의 변화를 그래프로 나타내었다. 이를 통해 확인할 수 있는 점은 Ridge와 Lasso 모두 t가 작아짐에 따라 모든 계수의 크기가 감소한다는 점이다. 그러나 Ridge의 경우 이 회귀 계수 값들이 0이 되진 않지만, Lasso는 예측에 중요하지 않은 변수가 더 빠르게 감소하며 t가 작아짐에 따라 에측에 중요하지 않은 변수가 0이 되는 것을 확인할 수 있다.

지금까지 확인한 Ridge와 Lasso를 비교하면 다음과 같다.

Lasso Limitation
Lasso의 한계점은, 변수들 간의 상관관계가 큰 경우 변수 선택과 예측의 성능이 저하된다는 것이다. 따라서 변수 간 상관관계를 반영할 수 있는 방법이 필요하다. 다음 그림을 확인해보면 변수 간의 상관관계가 높을 경우 boxplot의 box의 크기가 커져 회귀 계수들의 값의 차이가 커지는 것을 확인할 수 있다.

Elastic-Net
이러한 Lasso의 Limitation을 해결하기 위해 나온 모델이 Elastic Net이다. 이는 Ridge와 Lasso를 결합한 모델이다(L1- and L2-regularization). Elastic-Net은 상관관계가 큰 변수를 동시에 선택 혹은 배제하는 특성이 있다. Elastic-Net은 파라미터 람다1, 람다2를 선정하는 특별한 방법이 있진 않다. Grid Search를 통해 일정 범위 내로 두 파라미터를 조정하여 가장 좋은 예측 결과를 보이는 값을 선정하게 된다.

본 포스팅은 고려대학교 산업경영공학부 김성범 교수님 유튜브의 핵심 머신러닝 강의를 듣고 작성한 글입니다.