시각 패턴 인식을 위한 신경망 모델
순방향 신경망으로 MNIST 필기체 숫자를 인식하려면 28x28 이미지를 784 크기의 1차원 벡터로 변환해서 모델에 입력해야 한다. 2차원 이미지를 1차원으로 펼치면 어떤 숫자인지 인식하기 어렵다. 이는 공간 데이터를 1차원으로 변환하는 순간 형상 정보가 분산되기 때문에 정확한 패턴을 인식하기 어려운 것이다. 또한 이미지와 같은 고차원 데이터는 차원별로 크기가 조금씩만 커져도 전체 데이터 크기가 기하급수적으로 증가한다. 입력 데이터가 커질수록 더 많은 특징을 포함하기 때문에 그에 따라 모델의 파라미터 수가 급격히 증가한다. 따라서 순방향 신경망은 이미지 데이터를 처리하기에 효율적이지 않다.
CNN의 구조
현대의 CNN도 최초의 CNN 모델인 `LeNet-5`와 같이 컨벌루션 계층과 서브샘플링 계층이 번갈아 가면서 반복되고 완전 연결 계층으로 이어지는 구조다. 컨벌루션 계층은 컨벌루션 연산을 통해 이미지의 다양한 특징을 학습하며, 서브샘플링 계층은 풀링 연산을 통해 이미지의 크기를 줄여서 특징의 작은 이동에 대한 위치불변성을 갖도록 한다. CNN에서 수용 영역은 뉴런이 데이터를 전달받은 입력 이미지의 영역이다. 이는 컨벌루션 연산과 서브샘플링 연산이 더 많이 실행될수록 점점 넓어져 작은 영역의 단순한 특징부터 넓은 영역의 복잡한 특징까지 계층적으로 인식한다.
컨벌루션 연산
`Convolution`은 두 함수를 곱해서 적분하는 연산으로, 함수 f에 다른 함수 g를 적용하여 새로운 함수를 만들 때 사용한다. 두 연속 함수 f(t)와 g(t)가 있다고 할 때 두 함수의 컨벌루션 연산은 다음과 같은 적분식으로 정의한다. 이때 함수 g(t)는 `convolution filter` 또는 `convolution kernel`이라고 부른다. 여기서 변형하려는 함수와 컨벌루션 필터 함수의 역할을 반대로 해도 결과값은 동일하다.
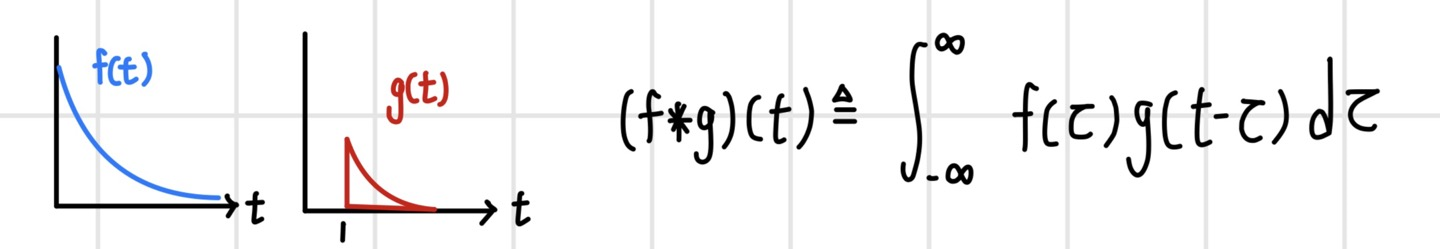
컨벌루션 연산을 위해 두 함수를 임시 변수에 대한 함수로 재정의하고 컨벌루션 필터 g(t)를 반전시킨다.
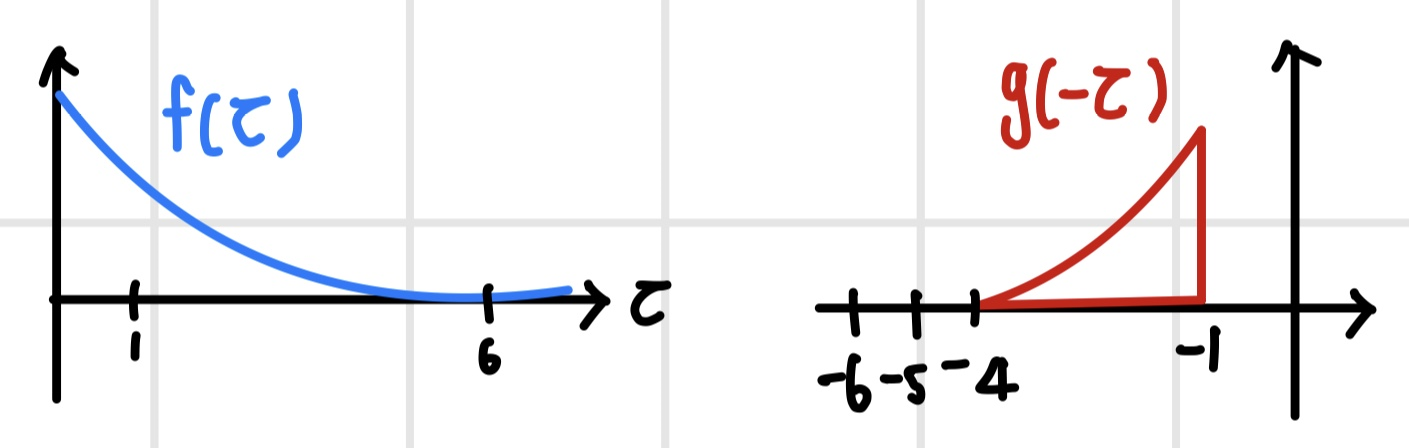
이후 컨벌루션 필터를 t만큼 이동하고 두 함수를 `내적(inner product)`한다. 내적은 두 함수의 곱을 적분한 형태이다. 내적 연산은 가중 합산 연산과 동일하므로 혼용이 가능하다.
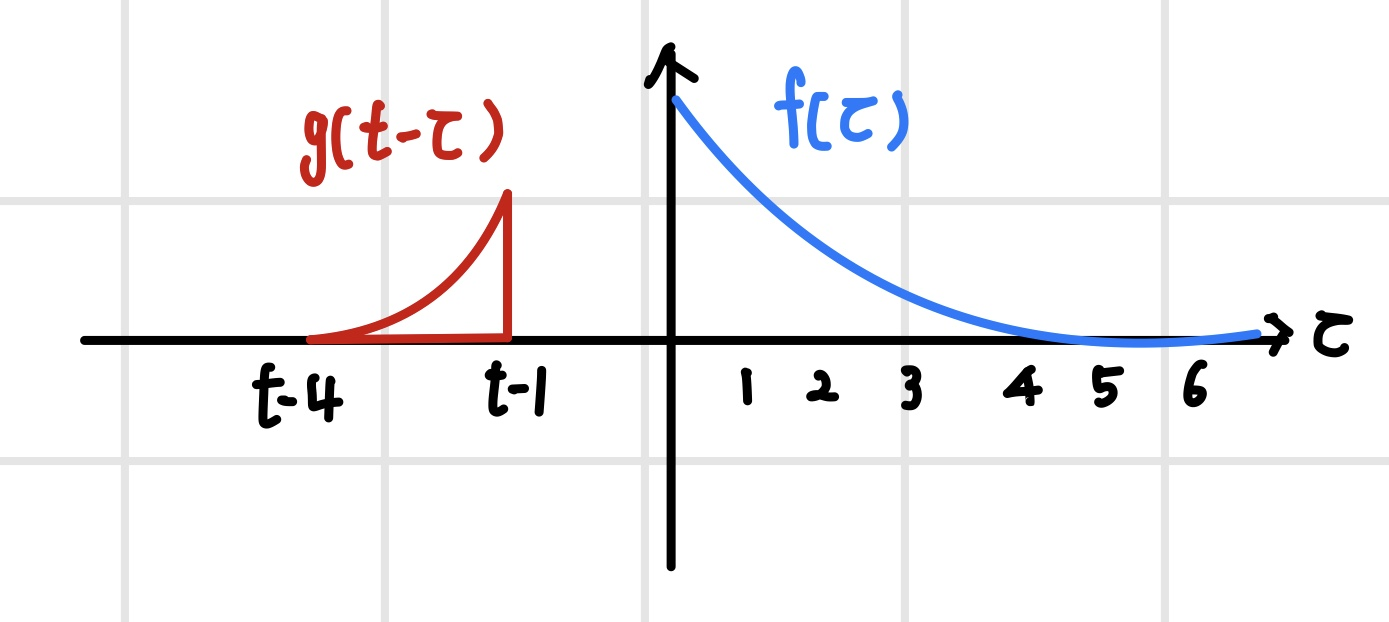
f(t)와 g(t)의 컨벌루션 연산은 시간 t에 대한 함수이기 때문에 두 함수를 t의 전구간 [-∞,∞]에서 내적을 하면 새로운 함수가 만들어진다. 여기서 함수 f는 t의 함수가 아니므로 고정되어 있고, 컨벌루션 필터는 시간축을 따라 전 구간에서 슬라이딩하며 내적한다.
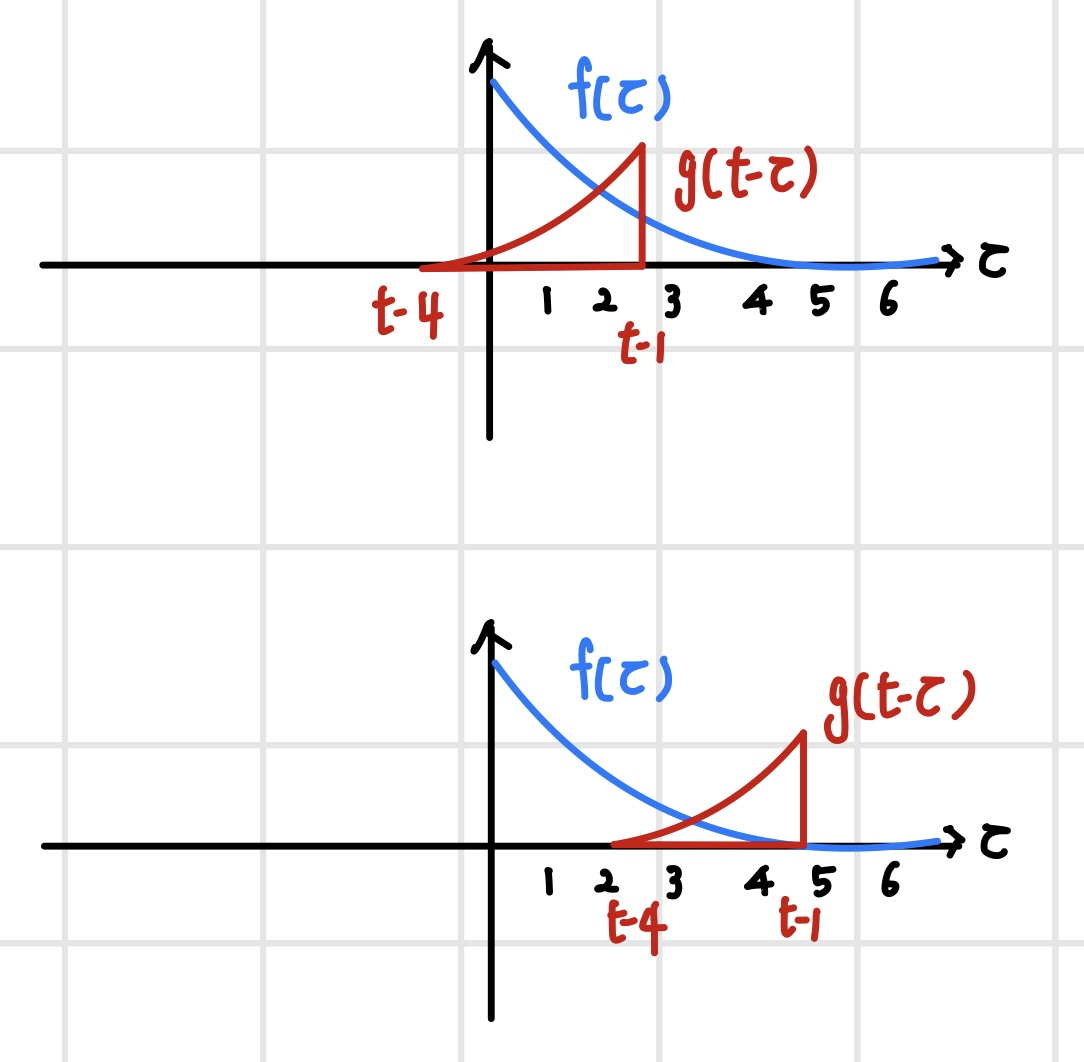
컨벌루션 연산과 유사한 연산이 `교차상관(cross correlation)` 연산이다. 이는 두 함수의 유사도를 측정하는 연산으로 함수 g를 반전시키지 않는다는 점만 제외하면 컨벌루션 연산과 동일하다. 따라서 컨벌루션 필터 g가 대칭인 경우 컨벌루션 연산과 동일하다. 이미지 컨벌루션을 할 때는 이름과 달리 교차상관 연산을 한다.
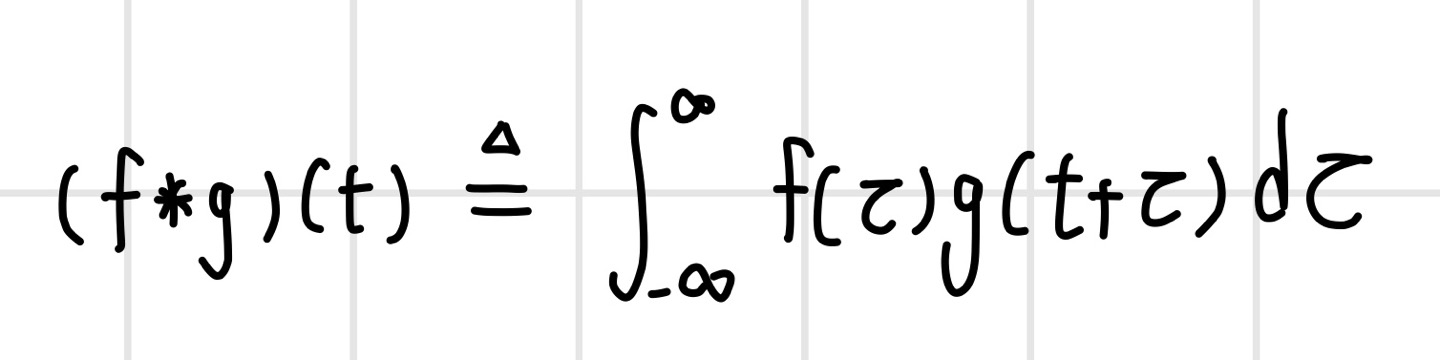
이미지 컨벌루션 연산
이미지에 대한 컨벌루션은 이미지의 특징을 추출하거나 이미지를 변환할 때 사용한다. 예를 들어 `경계선 검출(edge detection)`, `스무딩(smoothing)`, `샤프닝(sharpenng)`과 같은 이미지 처리가 있다. 이미지에 대한 컨벌루션 연산을 식으로 정의해 보면 다음과 같다. 2차원 이미지가 I이고 컨벌루션 필터가 K이다. 이미지는 입력 함수가 되고 컨벌루션 필터는 가중치 함수가 되어 픽셀 단위로 가중 합산을 한다. 여기서 함수의 인자 (i, j)는 픽셀 인덱스이다.
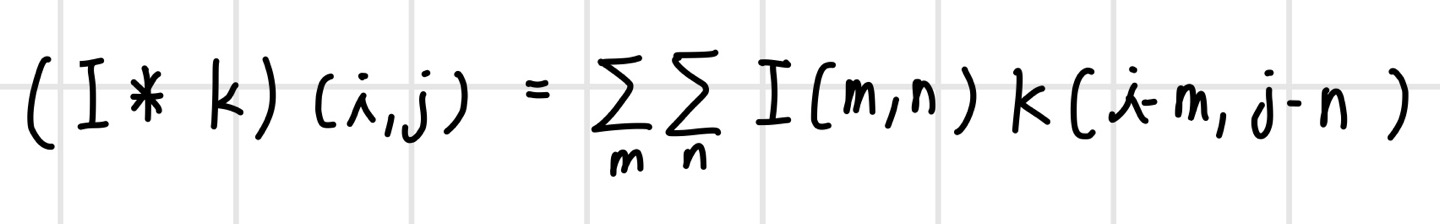
이미지 처리를 할 때는 필터를 반전시키지 않기 때문에 컨벌루션 연산이 아닌 교차상관 연산을 한다. 필터가 대칭적인 경우 두 연산은 동일하다. 컨벌루션 신경망은 교차상관 연산을 하지만 컨벌루션 연산을 한다고 표현한다. 컨벌루션 신경망은 둘 중 어떤 연산을 사용해도 그에 맞춰서 필터가 학습되는 만큼 결과에는 차이가 없다. 다만 필터를 반전하지 않는 편이 간단하므로 교차상관을 사용한다.
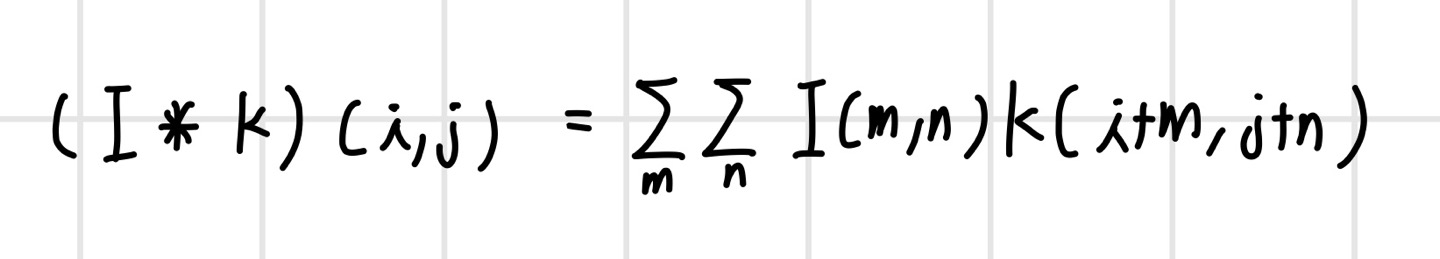
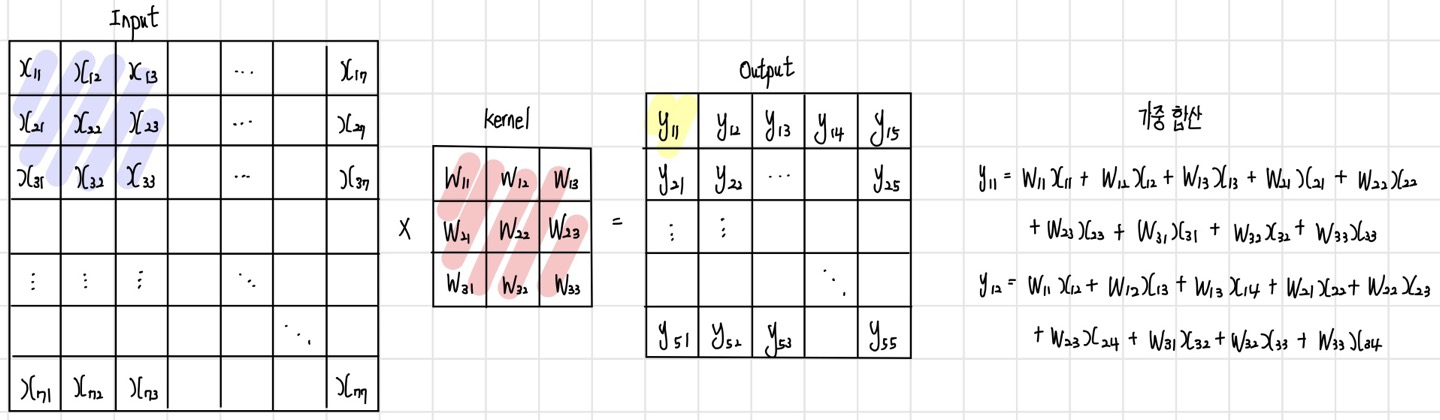
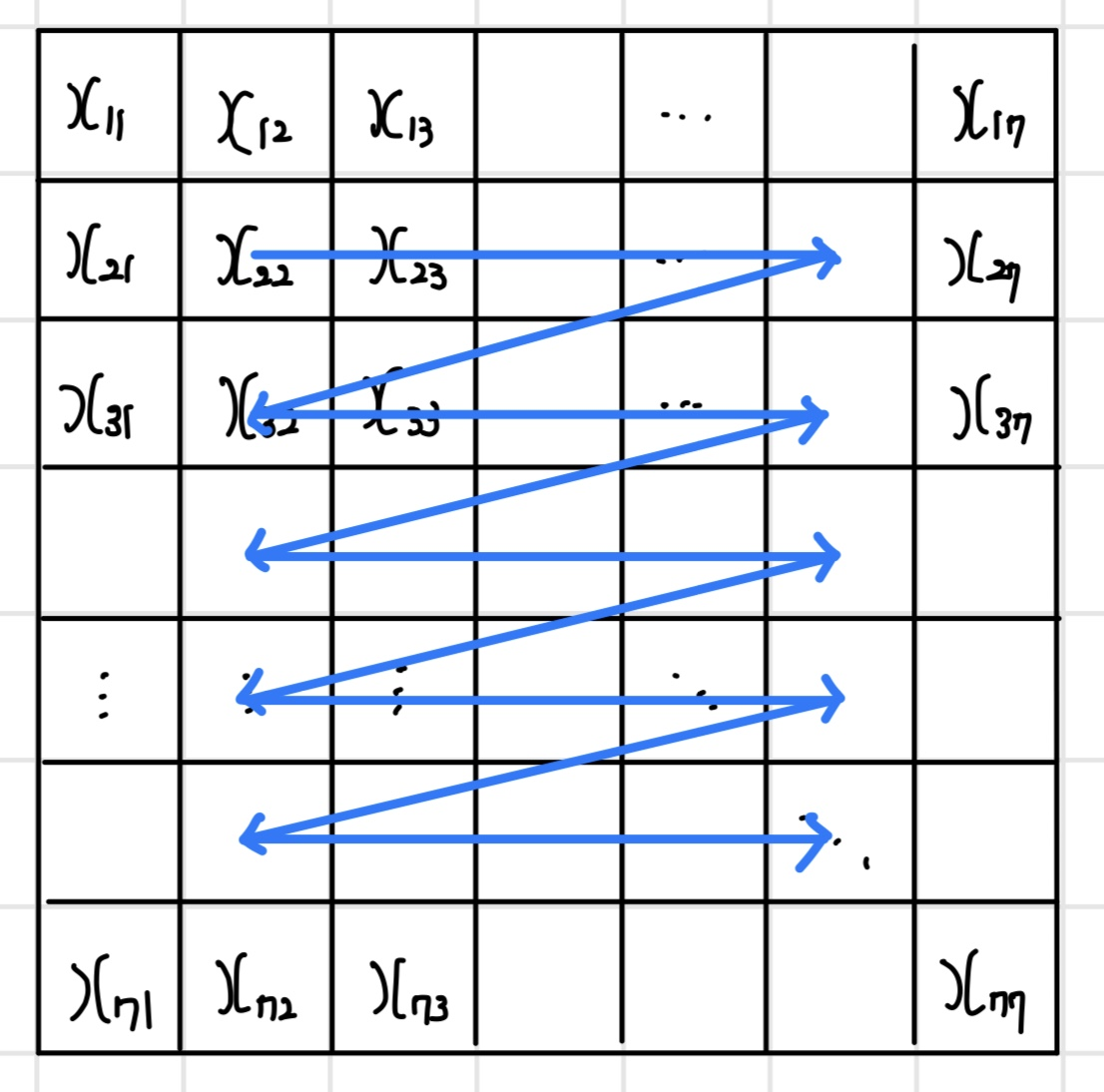
이미지 컨벌루션 연산 과정을 그림으로 확인해 보면 수식의 의미를 쉽게 이해할 수 있다. 다음 그림과 같이 7x7 이미지와 3x3 컨벌루션 필터가 있다고 하면, 첫 번째 가중 합산과 두 번째 가중 합산은 다음과 같은 식으로 계산된다. 이미지와 컨벌루션 필터를 왼쪽 위 모서리에 맞춰서 픽셀 단위로 가중 합산을 하면 새로운 이미지의 첫 번째 픽셀이 생성된다. 이후 컨벌루션 필터를 오른쪽으로 한 칸 슬라이딩한 뒤에 가중 합산으로 다음 픽셀을 생성한다. 같은 방식으로 한 줄에 대한 연산이 완료되면 다음 줄로 한 칸 내려가서 모든 줄에 대해 연산이 완료되면 컨벌루션 연산도 완료된다.
이미지에서 컨벌루션 필터를 슬라이딩할 때는 보통 가로 방향으로 한 줄을 슬라이딩하고 나서 세로 방향으로 한 칸씩 아래로 이동하는 순서로 진행된다. 다음 그림은 슬라이딩 순서를 나타내며, 파란 줄은 컨벌루션 필터의 중심에 해당한다.
이미지 컨벌루션 필터 설계 예시
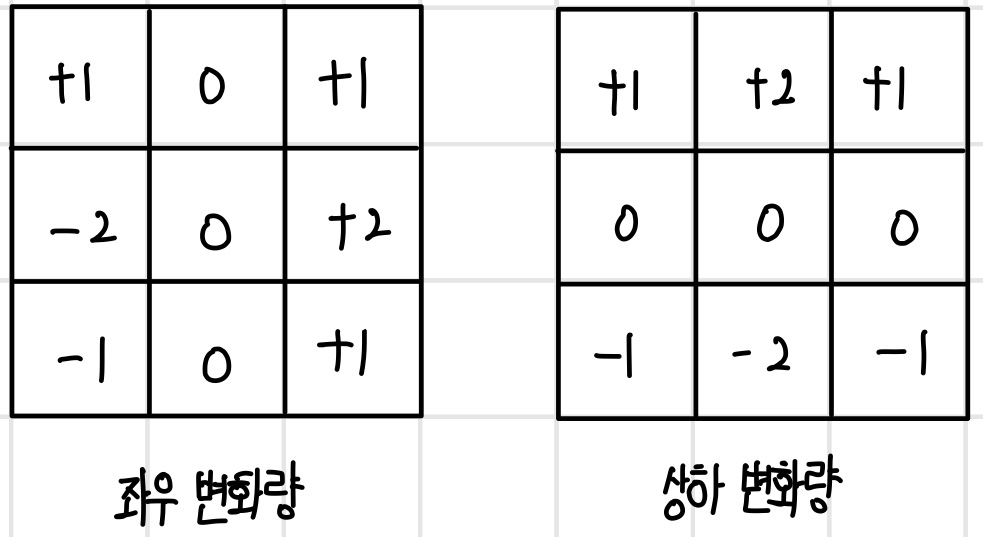
경계선 검출은 이미지에서 사물의 경계를 찾는 연산이다. 사물의 경계는 빛의 강도가 크게 변화하기 때문에 인접한 픽셀의 변화량을 계산하는 미분 필터를 사용한다. 미분 필터는 다음과 같이 좌우 또는 상하 픽셀값의 변화량을 계산하도록 설계한다.
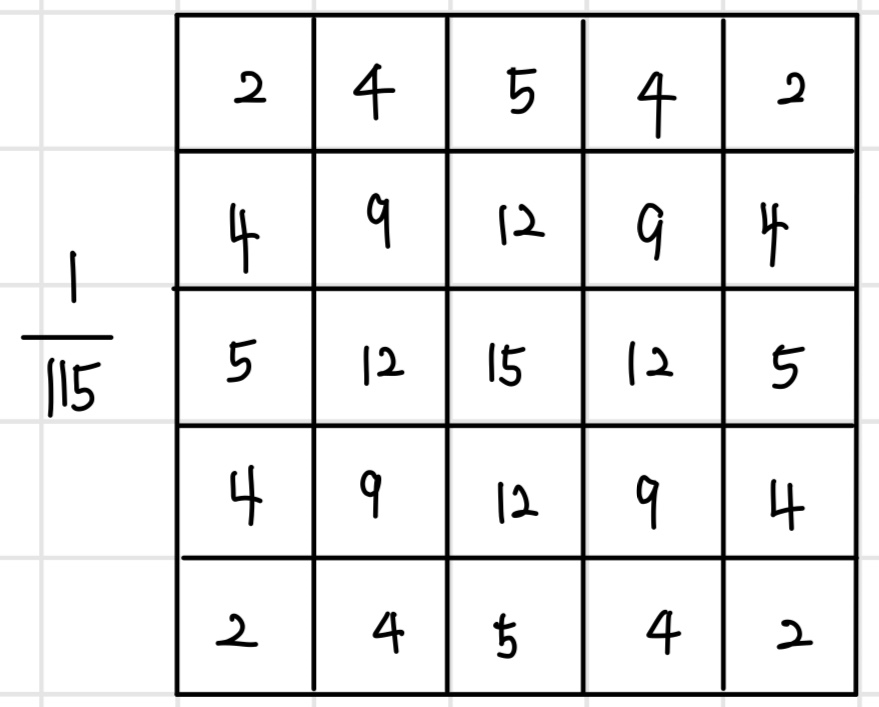
스무딩은 이미지의 색깔을 부드럽게 변하도록 만드는 연산이다. 스무딩을 적용하면 선명한 이미지가 몽환적인 느낌의 흐릿한 이미지로 바뀐다. 이를 위해 주변 픽셀을 가중 합산하며 주로 `가우시안 필터(Gaussian filter)`를 사용한다. 가우시안 필터는 가우시안 함수 형태로 가중치를 설계한 필터로, 필터의 중심에 가까울수록 큰 가중치를 갖고 멀어질수록 작은 가중치를 갖는다.
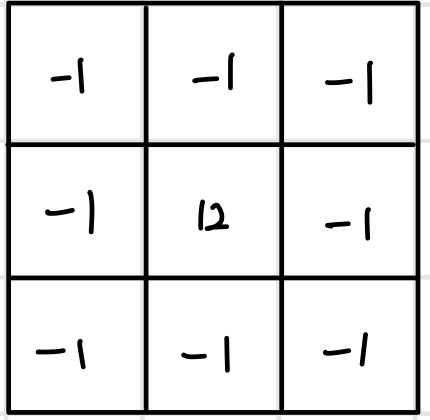
샤프닝은 이미지를 선명하게 만드는 연산이다. 선명한 윤곽을 갖는 이미지를 만들기 위해 2차 미분을 계산하는 `라플라스 필터(Laplace filter)`를 사용한다. 라플라스 필터는 좌우 또는 상하 픽셀값이 변화량에 대한 변화량을 계산하도록 설계한다. 이처럼 이미지 처리를 할 때는 연산의 목적에 맞게 컨벌루션 필터를 설계해야 한다.
컨벌루션 신경망의 컨벌루션 연산
컨벌루션 신경망은 이미지의 특징을 추출하기 위해 컨벌루션 필터를 학습하며, 특징의 추상화 수준에 따라 컨벌루션 연산을 여러 단계로 계층화해서 실행한다. 신경망 모델에서 컨벌루션 연산을 사용하는 방식은 다음과 같다.
- 데이터에 내포된 다양한 특징을 추출하도록 특징에 따라 다른 별도의 컨벌루션 필터를 둔다. 컨벌루션 필터별로 서로 다른 특징을 추출하므로, 데이터의 특징이 다양하다면 더 많은 필터가 필요하다. 하지만 이미지가 몇 개의 특징을 내포하는지 미리 알기 어려워 검증 과정을 통해 필터 개수를 조절한다.
- 컨벌루션 필터의 크기와 개수는 계층별로 특징의 추상화 수준에 따라 다르게 설계해야 한다. 추상화 수준이 높아질수록 특징이 세분화되므로 더 많은 종류의 필터가 필요하다.
- 컨벌루션 필터의 값은 데이터의 특징을 잘 추출하도록 학습을 통해 정한다. 즉, 미리 설계된 컨벌루션 필터를 사용하지 않고, 이미지의 특징에 따라 최적의 값으로 정의되도록 학습 과정에서 결정한다.
입력 데이터의 형태
이미지는 눈으로 볼 때는 2차원이지만, 색깔별로 빛의 강도를 나타내는 `채널(channel)`이 있기 때문에 3차원으로 표현한다. 컬러 이미지의 경우 RGB 채널을 가지며 투명도를 나타내는 `알파(alpha)` 채널까지 포함해서 RGBA로 표현하기도 한다. 흑백 이미지의 경우 한 개의 채널로 정의된다. 따라서 컨벌루션 신경망의 입력 데이터는 [Width] x [Height] x [Depth]로 표현되는 3차원 텐서이다. 여기서 [Width] x [Height]는 `공간 특징(spatial feature)`을 표현하며, [Depth]는 `채널 특징(channel feature)`을 표현한다. 흑백 이미지는 [Depth] = 1, 컬러 이미지는 [Depth] = 3, 투명도를 포함하는 컬러 이미지는 [Depth] = 4이다.
컨벌루션 필터의 형태
컨벌루션 필터도 [Width] x [Height] x [Depth]로 표현되는 3차원 텐서로 정의된다. 표준 컨벌루션 연산은 채널 방향으로 슬라이딩하지 않기 때문에 컨벌루션 필터의 [Depth]는 입력 데이터의 [Depth]와 동일해야 한다. 예를 들어, (32 x 32 x 3) 크기의 이미지에 대해 컨벌루션 연산을 하려면 (5 x 5 x 3) 크기와 같이 [Depth] = 3인 컨벌루션 필터가 필요하다.
컨벌루션 필터의 크기와 개수
뉴런의 수용 영역은 컨벌루션 필터의 크기에 따라 달라진다. 만약 모든 계층에서 작은 크기의 컨벌루션 필터를 사용한다면 수용 영역을 조금씩 늘려가며 특징을 학습하게 되고, 모든 계층에서 큰 크기의 컨벌루션 필터를 사용한다면 수용 영역을 빠르게 확장하며 특징을 학습하게 된다. 따라서 컨벌루션 필터의 크기에 따라 신경망의 성능이 달라지기 때문에 신경망의 성능이 최대화되도록 컨벌루션 필터의 크기를 정해야 한다. 일반적으로는 (5 x 5), (3 x 3), (7 x 7) 크기를 사용한다. 컨벌루션 필터의 개수는 필터마다 다른 특징을 학습하기 때문에 이미지의 특징이 다양할수록 더 많은 컨벌루션 필터를 사용해야 한다.
표준 컨벌루션 연산
컨벌루션 신경망에서 표준 펀벌루션 연산은 모든 채널에 대해 한꺼번에 가중 합산을 한다. 즉, 이미지와 필터가 채널이 딱 맞게 3차원으로 겹쳐진 상태에서 픽셀별로 가중 합산을 한다.
지역 연결을 갖고 가중치를 공유하는 뉴런
이미지와 컨벌루션 필터가 가중 합산 연산을 할 때마다 하나의 뉴런이 실행된다. 즉, 뉴런의 관점에서 보면 이미지 영역과 컨벌루션 필터가 가중 합산될 때 뉴런의 가중 합산 연산이 실행된 것이다. 그러나 이 뉴런은 입력 데이터의 모든 차원과 연결되는 것이 아닌 컨벌루션 필터와 겹쳐진 영역에만 연결되는 `지역 연결(local connectivity)`을 갖는다. 또한 뉴런의 가중치에 해당하는 컨벌루션 필터는 모든 뉴런에서 재사용되기 때문에 컨벌루션 신경망의 뉴런은 지역 연결을 갖고 가중치를 공유하는 뉴런이다.
액티베이션 맵의 생성
컨벌루션 연산 결과로 만들어지는 이미지를 `액티베이션 맵(activation map)`이라고 한다. 이는 입력 데이터의 특징을 추출한 결과이기 때문에 `피처 맵(feature map)`이라고도 한다. 액티베이션 맵의 픽셀은 각 뉴런의 출력이다. 따라서 한 계층에는 액티베이션 맵과 같은 3차원 텐서 형태로 뉴런이 모여있다고 생각할 수 있다. 이 뉴런은 컨벌루션 필터 크기만큼의 지역 연결을 가지며 입력 데이터의 지역 특성을 학습한다. 또한 컨벌루션 필터의 가중치를 공유하기 때문에 학습된 특징이 나타나면 위치에 상관없이 인식한다. 이러한 성질을 `이동등변성(translation equivariance)`이라고 한다.
만약 첫 번째 계층에 또 다른 컨벌루션 필터로 컨벌루션 연산을 한다고 하면, N개의 컨벌루션 필터가 있다면 각각의 필터로 컨벌루션을 하게 되므로 N개의 채널을 갖는 액티베이션 맵이 생성된다. 즉, 새로운 컨벌루션 필터로 컨벌루션을 할 때마다 액티베이션 맵이 추가되므로, 컨벌루션 필터의 개수와 액티베이션 맵의 채널 수는 동일하다.
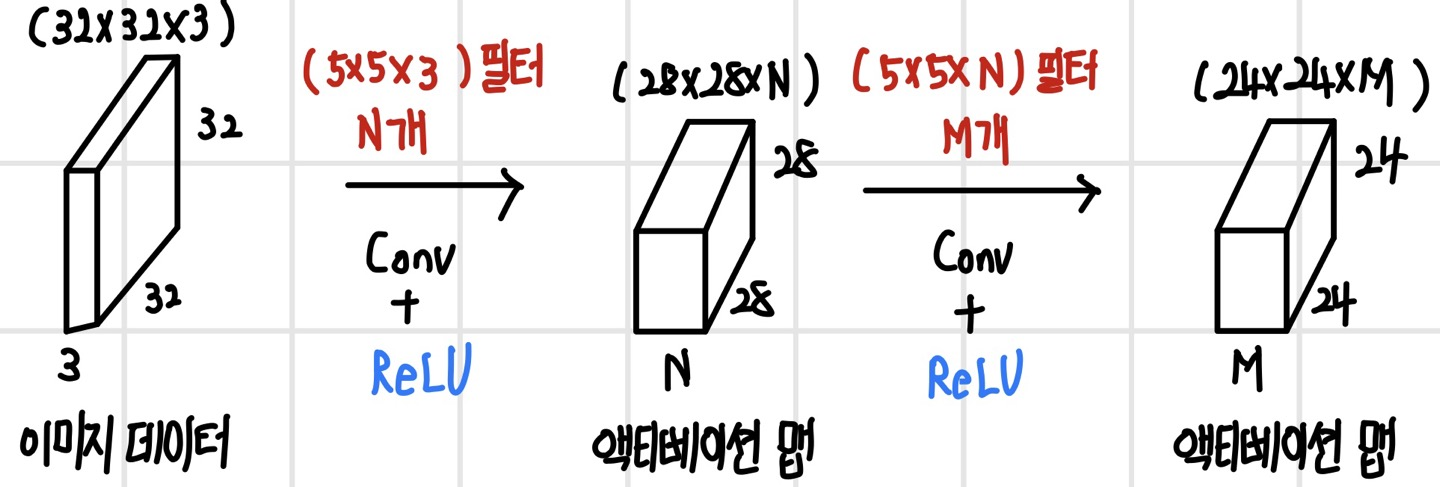
두 번째 계층의 컨벌루션 연산
첫 번째 계층에서 출력된 (28 x 28 x N) 크기의 액티베이션 맵은 두 번째 계층의 입력 데이터가 되어 또 다른 컨벌루션 연산을 수행한다. 이때 앞서 첫 번째 계층에서 입력 데이터인 이미지 데이터의 채널 수와 컨벌루션 필터의 채널 수가 동일해야 했던 것처럼 두 번째 계층에서도 입력 데이터인 (28 x 28 x N) 크기의 액티베이션 맵의 채널 수인 N과 두 번째 계층의 컨벌루션 필터의 채널 수는 동일하게 N이어야 한다. 또한 두 번째 계층의 컨벌루션 필터의 개수가 M개이면 채널의 수가 M개인 액티베이션 맵이 만들어진다. 결론적으로 두 번째 계층에서는 (28 x 28 x N) 크기의 입력 데이터를 M개의 (5 x 5 x M) 크기의 컨벌루션 필터로 컨벌루션 해서 (24 x 24 x M) 크기의 액티베이션 맵을 얻게 된다.
뉴런의 활성 함수 실행
각 계층의 뉴런은 액티베이션 맵과 동일한 3차원 텐서 형태로 배열되어 있다. 따라서 이 3차원 텐서에 활성 함수를 실행하면 모든 뉴런에 활성 함수가 일괄로 실행된다. 다음 그림과 같이 계층별로 컨벌루션 연산을 실행한 뒤에 활성 함수를 실행하면 뉴런의 기본 연산이 완료된다. 순방향 신경망의 계층과 비교해 보면 컨벌루션 신경망의 계층은 모든 입력 데이터와 출력 데이터가 1차원에서 3차원으로 확장되어 있고 뉴런 또한 3차원 배열로 확장되어 있다. 또한 뉴런은 컨벌루션 필터 크기의 지역 연결을 가지며, 같은 채널의 뉴런들은 컨벌루션 필터의 가중치를 공유한다.
컨벌루션 신경망에서 서브샘플링 연산
`서브샘플링(subsampling)`은 데이터를 낮은 빈도로 샘플링했을 때의 샘플을 근사하는 연산이다. 데이터가 이미지라면 이미지 크기를 줄이는 연산이 되어 `다운샘플링(downsampling)`이라고 부른다. 컨벌루션 신경망은 이미지 크기를 줄이기 위해 LeNet-5에서부터 `풀링(pooling)` 연산을 사용했다.
풀링 연산을 이용한 서브샘플링
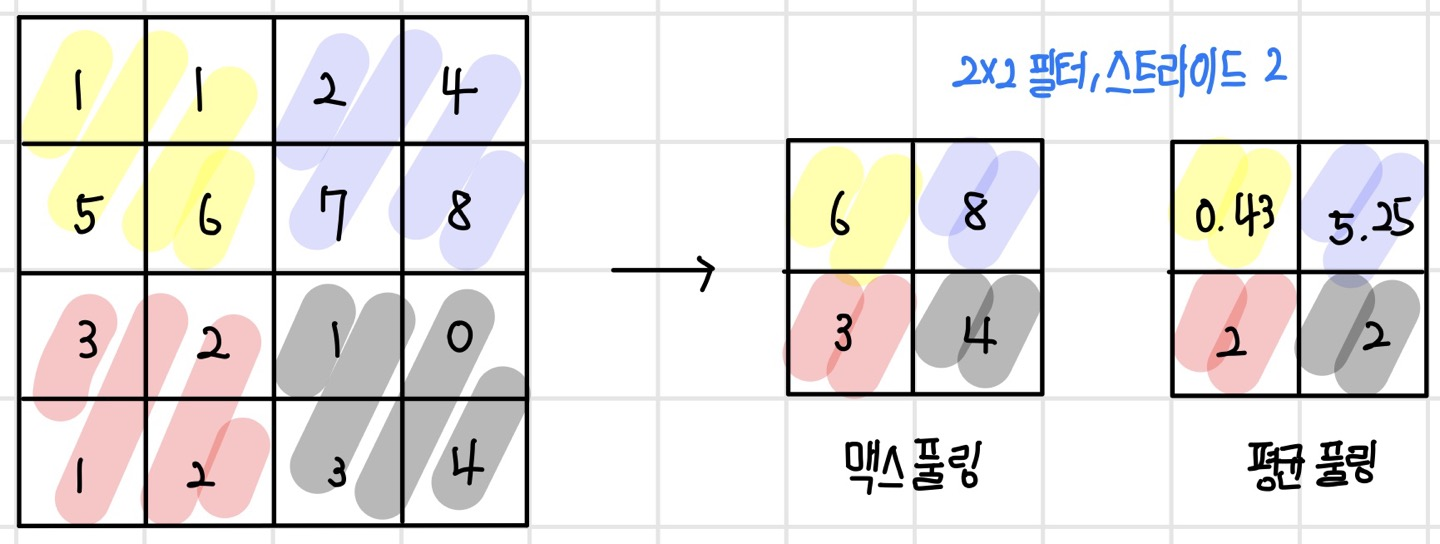
풀링 연산은 이미지상에서 풀링 필터를 슬라이딩하면서 요약 통계량을 구하는 연산이다. 풀링 연산에서는 주로 평균, 최댓값 같은 요약 통계량을 사용하며 최소, 가중 합산, L2 노름 등도 사용할 수 있다. 최댓값을 사용하는 풀링 연산을 `맥스 풀링(max pooling)`이라고 한다. 맥스 풀링은 입력 데이터의 가장 두드러진 특징을 추출한다. 또한 평균을 사용하는 풀링 연산을 `평균 풀링(average pooling)`이라고 한다. 평균 풀링은 입력 데이터의 평균적인 특징을 추출한다. 풀링 연산을 통해 서브샘플링을 하는 경우 보통 (2 x 2) 필터를 사용하고 필터 크기만큼 슬라이딩한다. (4 x 4) 이미지에 (2 x 2) 풀링 필터로 맥스 풀링과 평균 풀링을 수행하면 다음과 같다.
컨벌루션 신경망에서 풀링 연산
컨벌루션 신경망에서 풀링 연산을 할 때는 계층별로 풀링 필터의 크기와 슬라이딩 간격을 지정해 준다. 풀링 필터는 지정된 요약 통계량만 구하면 되기 때문에 컨벌루션 필터와 달리 학습을 따로 하지 않는다. 그러나 풀링 연산은 컨벌루션 연산과 같은 방식으로 슬라이딩하며 채널별로 요약 통계를 계산하기 때문에 채널 수는 유지된다. 다음 그림은 컨벌루션 연산과 활성 함수를 실행한 뒤에 풀링 연산까지 실행한 것이다.
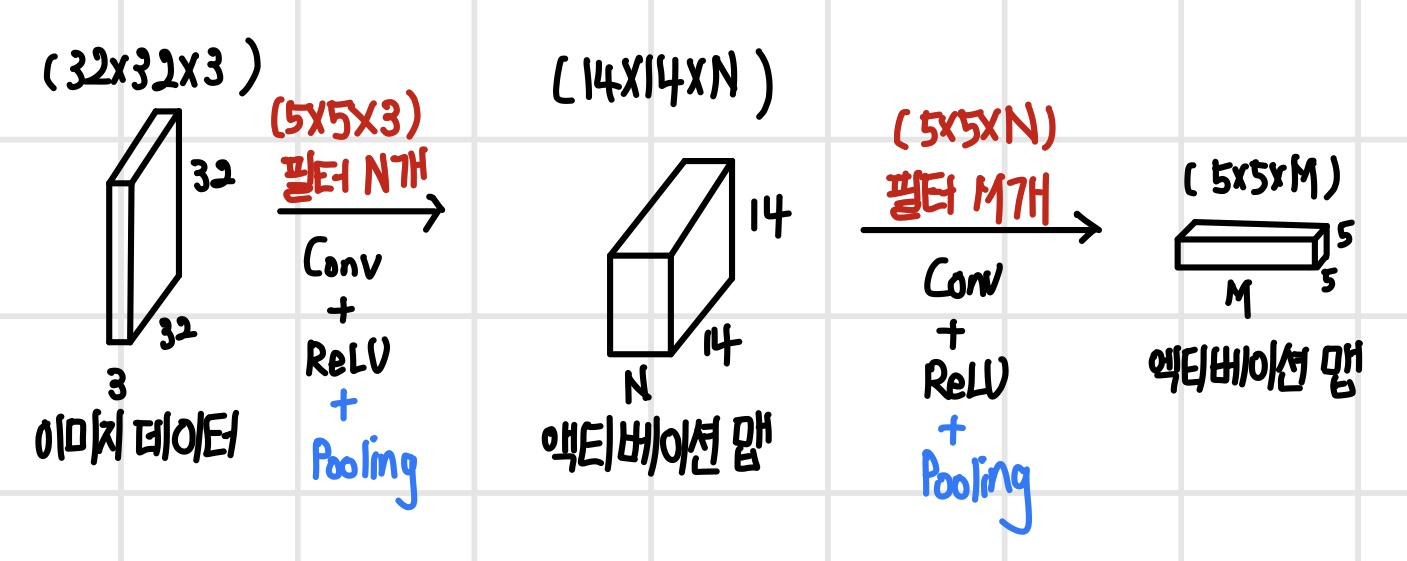
초기 컨벌루션 신경망 모델에서는 컨벌루션 연산을 한 번 하고 풀링 연산을 했지만, 최근에 나오는 컨벌루션 신경망 모델에서는 계층을 깊게 쌓기 위해서 컨벌루션 연산을 여러 번 하고 나서 풀링 연산을 수행한다. 풀링 필터의 크기는 (2 x 2) 크기를 많이 사용하지만 컨벌루션 신경망의 성능이 최대화되도록 정의해야 한다.
계층이 깊어지면 뉴런의 수용 영역이 넓어지며 서브샘플링을 하면 수용 영역은 더 빠르게 넓어진다. 여기서 서브샘플링을 하면 이미지 크기가 줄어들기 때문에 공간 특징이 손실되므로 대신 컨벌루션 필터 개수를 늘려서 다양한 특징을 학습하게 만든다. 특히 계층이 깊어질수록 데이터는 추상화된 전역적인 특징으로 변하며, 추상화된 전역적 특징은 세분되고 다양해지므로 채널 특징을 늘려줘야 정확하게 인식할 수 있다. 따라서 대부분의 컨벌루션 신경망은 계층이 깊어질수록 액티베이션 맵의 크기는 줄어들지만 채널 수는 늘어나는 형태를 보인다.
스트라이드(stride)
컨벌루션 연산과 풀링 연산을 할 때 필터의 슬라이딩 간격을 `스트라이드(stride)`라고 한다. 대부분 서브샘플링 없이 특징을 학습할 때는 한 칸씩 슬라이딩하고, 서브샘플링을 할 때는 두 칸씩 슬라이딩하지만, 종종 슬라이딩 간격을 더 크게 두기도 한다. 컨벌루션 연산의 출력의 크기는 간단한 수식으로 나타낼 수 있다.
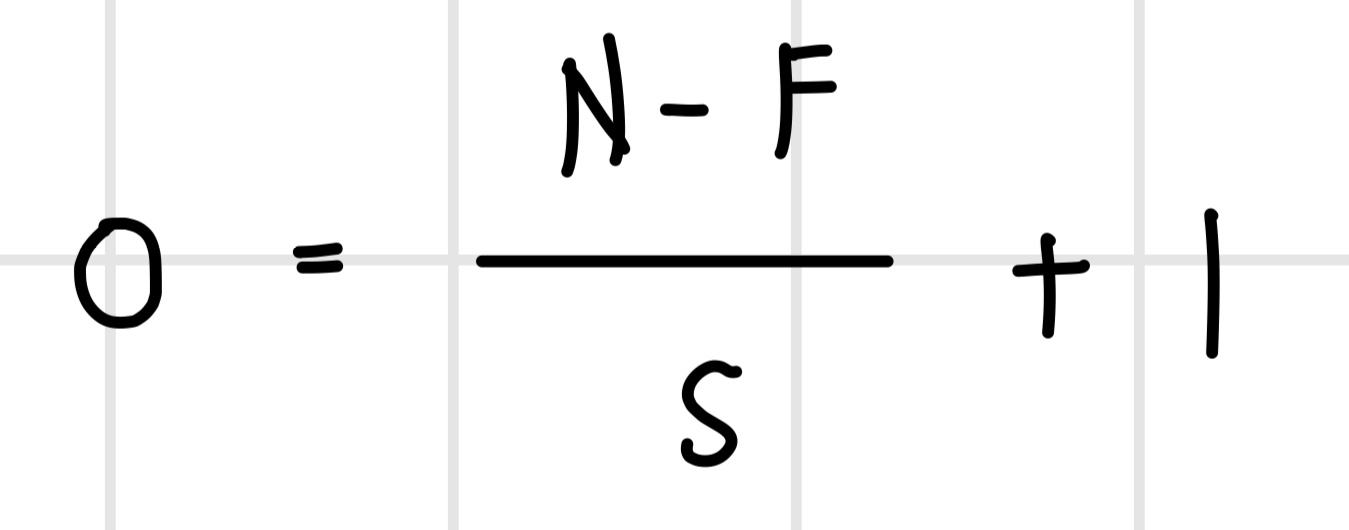
- N : 입력 데이터의 크기
- F : 컨벌루션 필터 크기
- S : 스트라이드
- O : 출력 데이터 크기
패딩(padding)
컨벌루션 연산을 하면 컨벌루션 필터가 입력 이미지 안에서만 슬라이딩하기 때문에 출력 이미지의 크기는 입력 이미지의 크기보다 작아질 수밖에 없다. 여기서 이미지 크기는 컨벌루션 필터의 크기 F - 1 픽셀씩 작아진다. 이로 인해 컨벌루션 연산을 계속 진행하면 어느 순간 컨벌루션 연산을 할 수 없는 크기로 변한다. 이는 이미지 크기와 컨벌루션 필터의 크기에 따라 컨벌루션 연산 횟수가 제한됨을 의미한다. 이러한 경우 컨벌루션 계층 수가 제한되기 때문에 원하는 대로 신경망을 깊게 만들 수 없다. 따라서 컨벌루션 연산 이후에도 이미지 크기를 유지하기 위해 이미지에 픽셀을 추가해서 크기를 늘려줘야 하는데, 이를 `패딩(padding)`이라고 한다.
컨벌루션 연산 후에도 이미지 크기를 유지하려면 줄어들 픽셀만큼 이미지 패딩을 하면 된다. 앞서 컨벌루션 연산 후에 F - 1 픽셀만큼 이미지가 작아진다면 이미지에 F - 1 픽셀을 패딩한다. 이렇게 하면 컨벌루션 연산 이후 이미지 데이터의 크기도 유지되고, 컨벌루션 연산 횟수의 제한이 사라져 신경망의 계층도 깊게 쌓을 수 있다. 패딩을 하고 컨벌루션 연산을 했을 때 출력 이미지의 크기는 다음 식으로 계산될 수 있다. 새롭게 패딩을 나타내는 변수 P가 추가되었다.
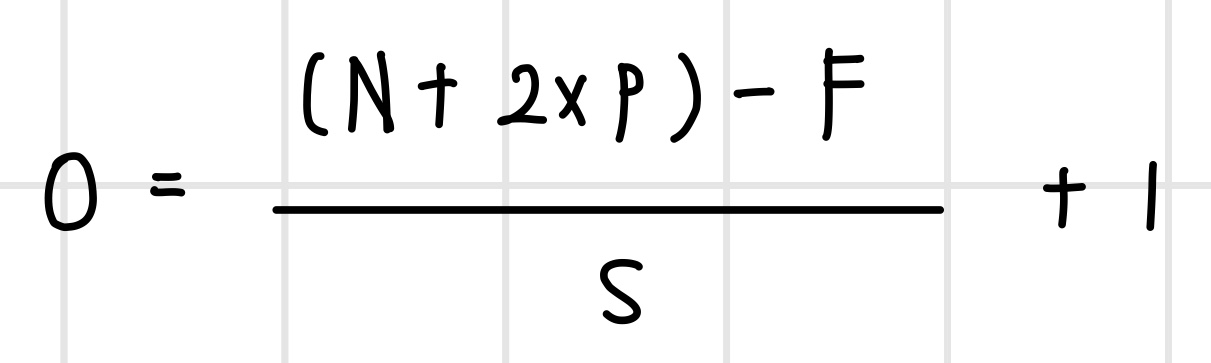
컨벌루션 연산 이후 이미지 크기를 유지하기 위한 패딩 크기는 다음과 같이 계산할 수 있다.
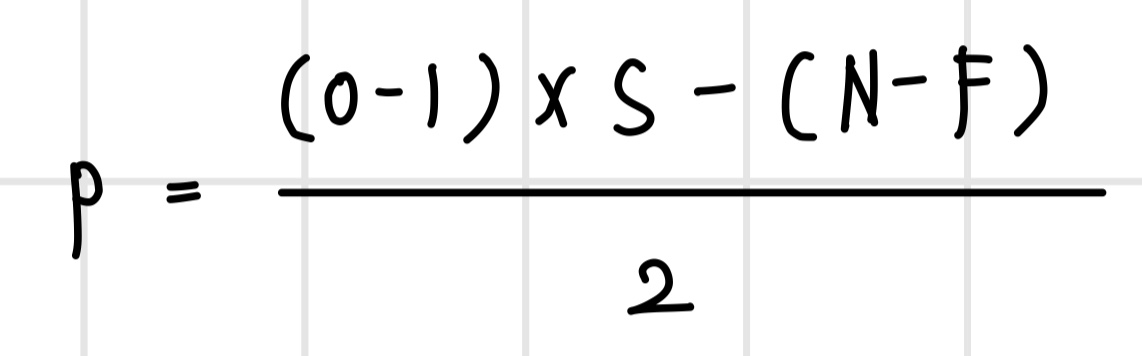
컨벌루션 신경망의 가정 사항
컨벌루션 신경망은 뉴런이 지역 연결을 갖는 모델이므로 파라미터를 일부만 사용한다. 사용하지 않는 파라미터는 해당 파라미터의 확률이 없는 것으로 간주하는 `매우 강한 사전 분포(infinitely strong prior)`를 가정하는 것이다. 이런 가정에서 컨벌루션 연산과 풀링 연산이 정의되었기 때문에 컨벌루션 신경망은 `희소 연결(sparse connectivity)`을 갖고 `파라미터 공유(parameter sharing)`를 하는 구조를 이루며 그에 따라 `이동등변성(translation equivariance)`과 `위치불변성(positional invariance)`를 갖는다.
컨벌루션 연산의 성질
컨벌루션 연산은 일부 파라미터를 사용하지 않는 매우 강한 사전 분포를 가정한다. 컨벌루션 연산 과정에서 컨벌루션 필터는 입력 데이터와 겹치는 영역에만 연결되고 나머지 영역에서는 연결이 없는 희소 연결을 가진다. 또한 동일한 컨벌루션 필터로 컨벌루션 연산을 하므로 같은 계층의 모든 뉴런은 파라미터를 공유한다. 컨벌루션 신경망은 희소 연결을 가지고 파라미터 공유를 하므로 위치에 상관없이 동일한 지역 특징을 인식할 수 있는 이동등변성을 가진다.
희소 연결 성질
만약 매우 강한 사전 분포가 가정되지 않았다면 뉴런이 모든 입력에 대해 연결을 갖는 `완전 연결(full connectivity)`을 가진다. 입력이 m개이고 뉴런이 n개이면 전체 파라미터 수는 O(m x n)이 된다. 그러나 매우 강한 사전 분포가 가정된 컨벌루션 신경망에서는 뉴런이 입력 데이터의 국소 지역에만 연결되는 희소 연결을 가진다. 이 경우 뉴런의 개수가 n이고 뉴런에 연결된 입력의 개수가 k이며 전체 파라미터 수는 O(n x k)이다. 여기서 k개는 완전 연결의 입력 m보다 아주 작은 수이기 때문에 희소 연결을 가지면 파라미터가 줄고 메모리와 계산이 절약된다.
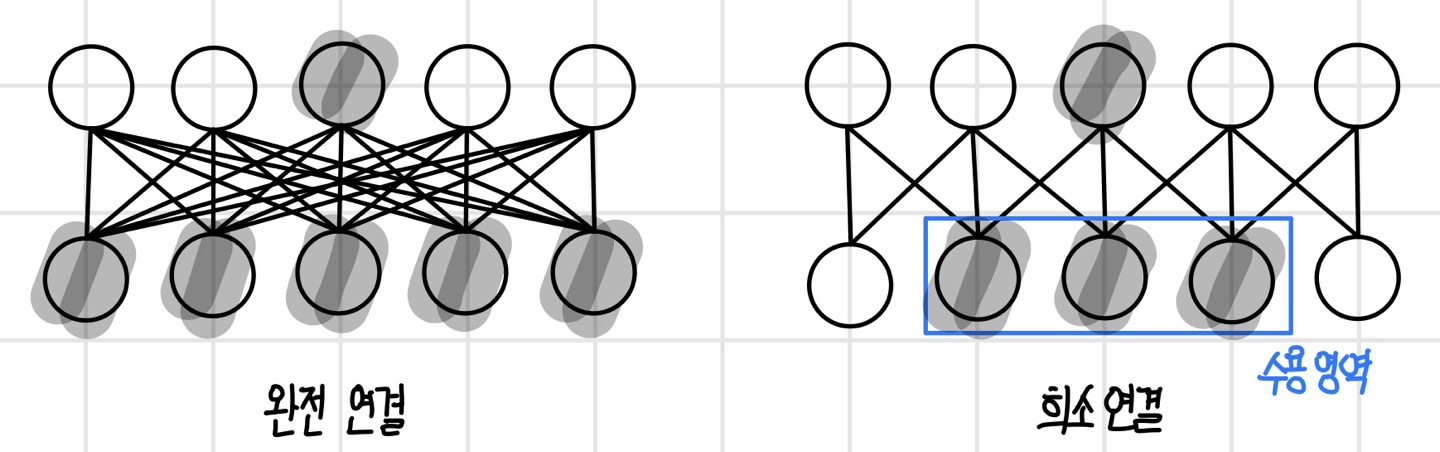
파라미터 공유 성질
희소 연결 상태에서 파라미터를 공유하면 뉴런의 개수가 n이고 뉴런에 연결된 입력의 개수가 k일 때 전체 파라미터의 수가 O(k)가 된다. 파라미터 수가 입력과 뉴런 개수에 더 영향을 받지 않게 되면서 메모리와 계산이 극적으로 감소한다.
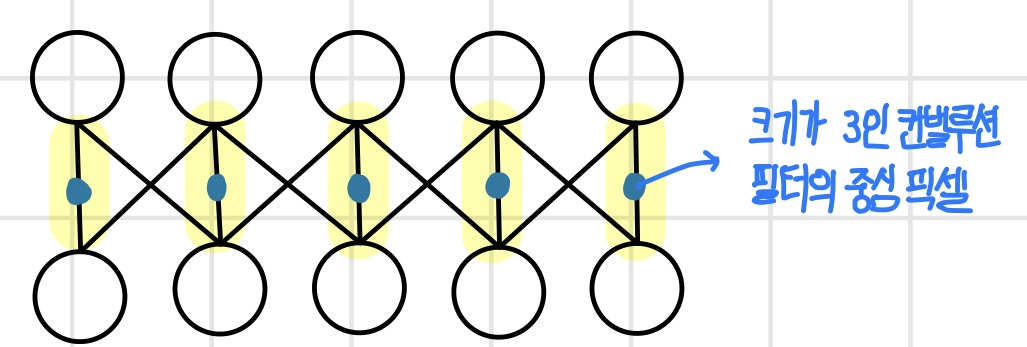
이동등변성
이동등변성은 희소 연결과 파라미터 공유 성질로 인해 생기는 컨벌루션 연산의 주요 성질로 위치에 상관없이 특징을 인식하는 성질이다. 만약 입력 데이터를 이동한다면, 입력 데이터에서 이동한만큼 추출된 특징도 이동해서 나타난다. 즉, 이동변동성은 특징이 어느 위치에 나타나든 동일한 방식으로 특징을 인식하는 성질을 말한다. 컨벌루션 연산은 이동등변성을 가지므로 이미지상에 같은 패턴이 어떤 위치에 나타나더라도 모두 추출할 수 있다.
컨벌루션 신경망은 컨벌루션 연산의 이동등변성을 이용해서 동시에 여러 특징을 추출하고, 그다음 계층에서 이들을 조합한 더 복잡한 특징을 추출하는 방식으로 구성된다. 낮은 계층에서는 지역적인 특성을 인식하더라도 계층이 높아질수록 수용 영역이 넓어지면서 전역적인 특징을 인식할 수 있다. 최종적으로 출력 계층에서 전체적인 특징을 인식한다. 그러나 컨벌루션 연산은 이동 변환에 대해서는 등가 성질을 갖지만 크기 조정이나 회전에 대해서는 등가 성질을 갖지 않는다.
풀링 연산의 성질
풀링 연산 역시 매우 강한 사전 분포를 가정하므로 수용 영역 외에 파라미터는 사용하지 않는다. 이로 인해 풀링 연산은 위치불변성을 가진다. 예를 들어 맥스 풀링의 경우, 최댓값이 왼쪽으로 한 칸 이동하든 오른쪽으로 한 칸 이동하든 결과는 동일하다. 이처럼 입력이 아주 작게 이동했을 때 출력이 바뀌지 않는 성질을 위치불변성이라고 한다. 위치불변성은 특징의 정확한 위치보다 특징의 존재에 대해 관심이 많을 때 유용하므로 주로 인식 모델에서 활용한다.
개선된 컨벌루션 연산
표준 컨벌루션 연산에는 다음과 같은 몇 가지 성능적인 한계가 있다. 이러한 표준 컨벌루션 연산의 한계를 극복하기 위해 새로운 컨벌루션 방법들이 제안되어 왔다.
- 3차원 공간에서 한꺼번에 가중 합산을 하므로 필터도 크고 계산량도 많으며, 파라미터 수도 많다.
- 죽은 채널이 발생해도 알기 어렵다. 채널이 죽으면 의미 있는 특징이 생성되지 않기 때문에 출력에 대한 영향이 사라지고 성능이 낮아진다.
- 여러 채널에 대해 한꺼번에 연산하기 때문에 공간 특징과 채널 특징이 구분되지 않는다. 특히 채널 간 상관관계가 낮은 채널은 마치 잡음과 같아 학습 속도를 떨어뜨린다.
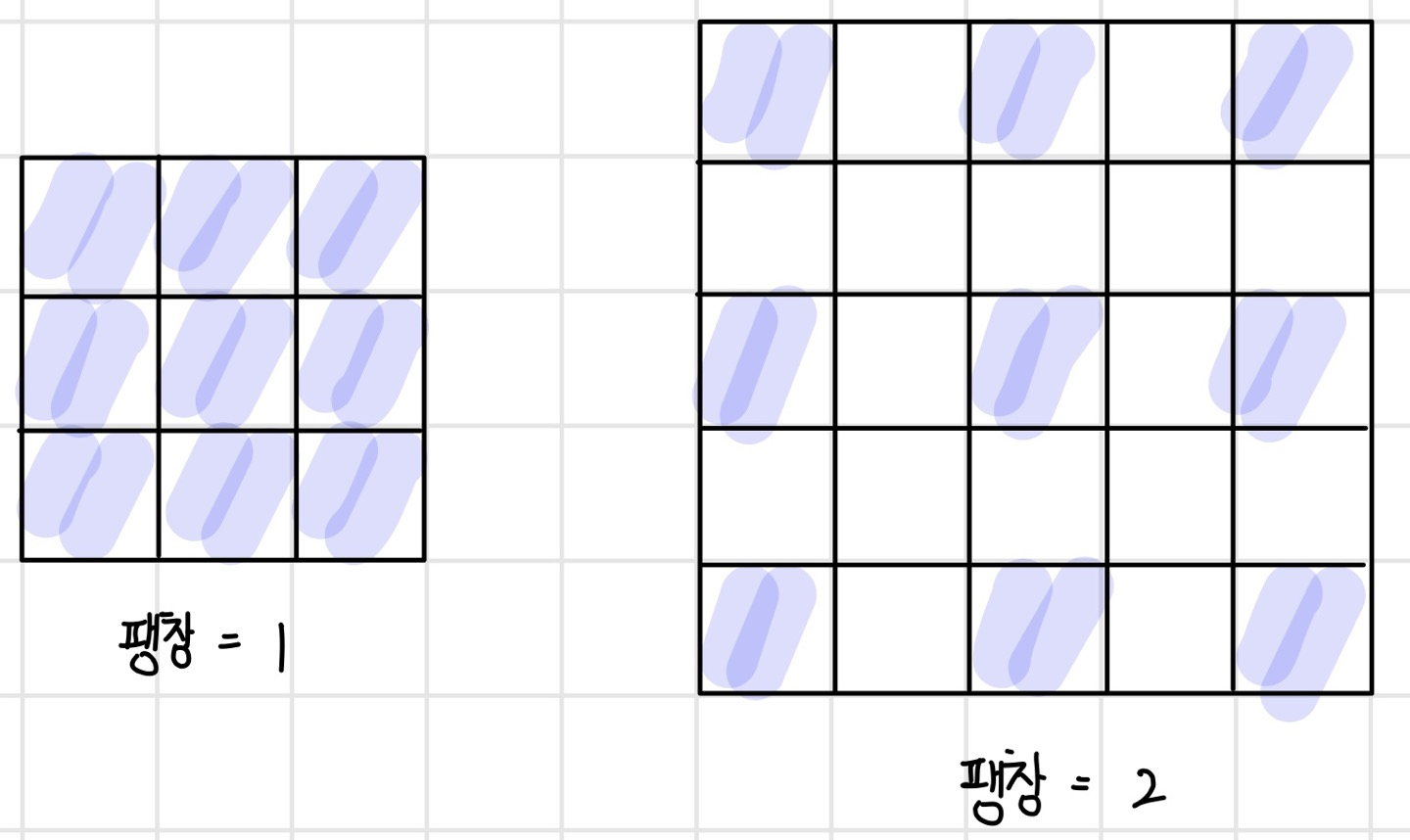
팽창 컨벌루션(dilated convolution)
신경망에서 뉴런의 수용 영역을 넓히기 위해선 컨벌루션 필터의 크기를 키우거나, 신경망의 깊이를 늘리거나, 서브샘플링 계층을 추가하면 된다. 그러나 컨벌루션 필터의 크기를 키우거나 신경망의 깊이를 늘리면 파라미터 수와 계산량이 많아진다는 문제점이 있다. 서브샘플링 계층을 추가하는 경우에는 이미지의 공간 특징이 손실되기 때문에 `세그멘테이션(segmentation)`과 같이 공간 특징을 활용하는 모델의 성능에 좋지 않은 영향을 끼친다.
파라미터 수와 계산량을 늘리지 않고 공간 특징을 유지하면서 수용 영역을 넓히기 위한 한 가지 방법으로 컨벌루션 필터의 수용 픽셀 간격을 띄워서 필터를 넓게 만드는 방법이 있다. 다음 그림과 같이 컨벌루션 필터의 수용 픽셀 수는 동일해도 픽셀 사이의 간격을 넓히면 수용 영역을 넓힐 수 있다. 이러한 종류의 컨벌루션 필터를 `팽창 컨벌루션 필터(dilated convolution filter)`라고 하며 팽창 컨벌루션 필터로 컨벌루션 하는 방법을 `팽창 컨벌루션(dilated convolution)`이라고 한다. 또한 수용 픽셀 간의 간격을 `팽창(dilation)`이라고 하며, 팽창을 크게 할수록 수용 영역이 넓어진다. 그러나 서브샘플링 대신 팽창 컨벌루션을 사용하면 공간 특징을 잘 유지할 수 있지만, 액티베이션 맵의 크기가 줄어들지 않기 때문에 메모리 사용량이 증가한다는 단점이 있다.
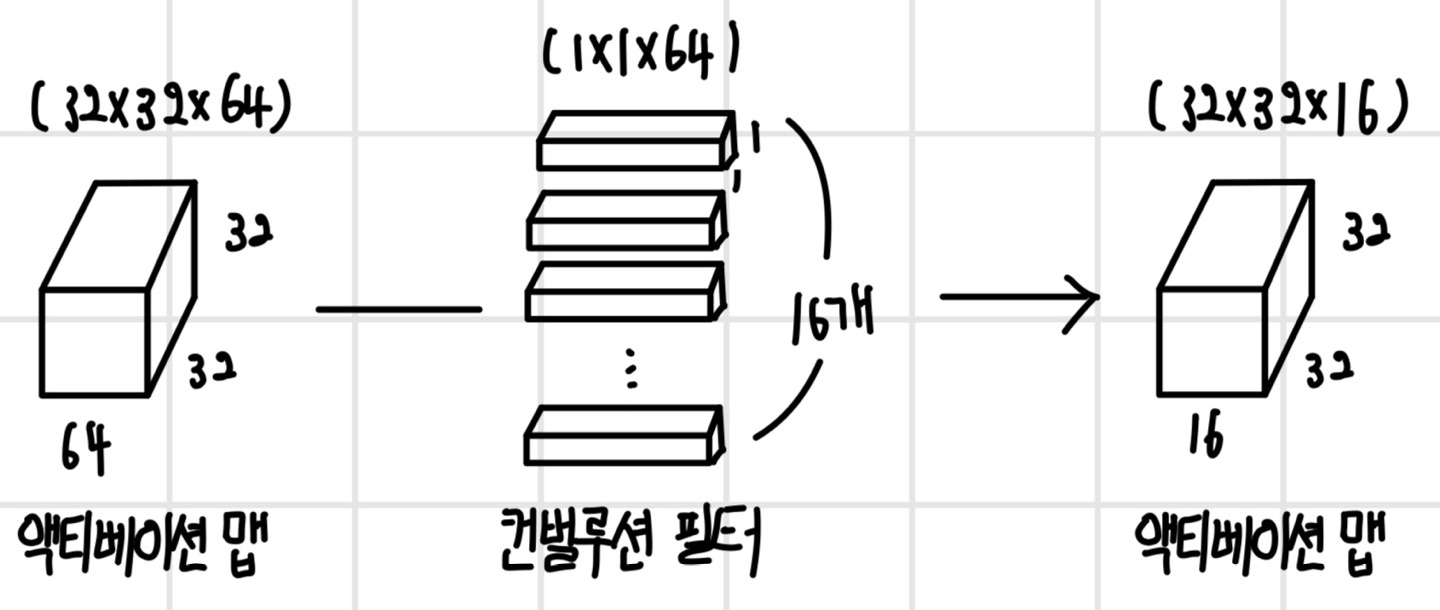
점별 컨벌루션(pointwise convolution)
`점별 컨벌루션(pointwise convolution)`은 가로 x 세로 크기가 (1 x 1)인 컨벌루션 필터를 사용하기 때문에 `1 x 1 컨벌루션`이라고 부르기도 한다. 점벌 컴벌루션은 픽셀별로 채널에 대해서만 컨벌루션하기 때문에 액티베이션 맵의 가로 x 세로 크기는 변하지 않고 채널 수만 달라진다. 점별 컴벌루션을 사용하면 채널 특징을 학습할 수 있으며 죽은 채널의 영향을 줄일 수 있다. 또한 채널 수를 줄이거나 늘릴 수 있어서 컨벌루션 계산량을 조절할 때 사용한다. 점별 컨벌루션은 `인셉션(inception)`, `레즈넷(ResNet)`, `모바일넷(MobileNet)`, `스퀴즈(SqueezeNet)`과 같은 CNN 모델에서 사용한다.
그룹 컨벌루션(grouped convolution)
`그룹 컨벌루션(grouped convolution)`은 채널을 여러 그룹으로 나눠서 컨벌루션하는 방식이다. 표준 컨벌루션보다 파라미터와 계산이 절약되며, 채널 간에 상관관계를 갖는 구조를 학습할 수 있다. `알렉스넷(AlexNet)`에서 두 개의 GPU 모델을 병렬 처리하기 위해 처음 제안되었으며 최근에는 `레즈넥스트(ResNext)`에서 사용한다. 표준 컨벌루션의 경우 인접한 두 계층의 컨벌루션 필터 간에 상관관계가 잘 생기지 않지만, 그룹 컨벌루션은 인접한 두 계층의 필터 그룹 간에 높은 상관관계가 있으며 구조적인 학습이 가능하다. 이로 인해 상관관계가 낮은 채널 간에는 연결되어 있지 않기 때문에 파라미터 수가 줄어들고 과적합이 방지되는 정규화 효과가 생긴다.
깊이별 컨벌루션(depthwise convolution)
표준 컨벌루션은 여러 채널에 대해 한꺼번에 컨벌루션 연산을 수행하기 때문에 채널별로 공간 특징을 학습할 수 없다. `깊이별 컨벌루션(depthwise convolution)`은 각 채널의 공간 특징을 학습할 수 있도록 채널별로 컨벌루션 연산을 수행하고 그 결과를 다시 결합한다. 깊이별 컨벌루션은 입력과 출력의 채널 수가 동일하며 표준 컨벌루션보다 파라미터와 계산이 절약된다. 그룹 컨벌루션의 채널 수가 1개이면 깊이별 컨벌루션과 같아 그룹 컨벌루션의 특별한 경우로 볼 수 있다.
깊이별 분리 컨벌루션(depthwise seperable convolution)
`깊이별 분리 컨벌루션(depthwise seperable convolution)`은 깊이별 컨벌루션과 점별 컨벌루션을 결합한 형태이다. 표준 컨벌루션 연산보다 8~9배 정도 계산량이 줄어든다. 깊이별 분리 컨벌루션은 모바일넷(MobileNet)에서 사용한다.
셔플 그룹 컨벌루션(shuffled grouped convolution)
그룹 컨벌루션은 같은 채널 그룹 안에서만 정보가 흐르고 그룹 간에 서로 정보를 교환하지 않는다. 하지만 채널 그룹 간에 정보를 교환하면 표현이 강화될 수 있는데 이는 `셔플넷(ShuffleNet)`의 `셔플 그룹 컨벌루션(shuffled grouped convolution)`으로 제안되었다. 셔플 그룹 컨벌루션은 주기적으로 그룹 간에 정보가 교환되도록 만든 그룹 컨벌루션 방식이다.
공간 분리 컨벌루션(spatially seperable convolution)
`공간 분리 컨벌루션(spatially seperable convolution)`은 정사각형 컨벌루션 필터를 가로 방향 필터와 세로 방향 필터로 인수분해한 방법이다. 이 방식은 인셉션(Inception) V3와 V4에서 사용한다. 공간 분리 컨벌루션은 계산량을 낮출 수는 있지만 모든 컨벌루션 필터를 인수분해할 수 없는 만큼 최적해가 아닌 준최적해(sub-optimal solution)를 찾을 수도 있다.
업샘플링(upsampling) 연산
컨벌루션 신경망에는 이미지 크기를 줄이는 연산뿐만 아니라 키우는 연산도 필요하다. 이미지 크기를 키우는 연산을 `업샘플링(upsampling)` 연산이라고 하며 주로 이미지 생성 모델이나 세그멘테이션 모델에서 사용한다. 이미지 생성 모델은 저차원의 잠재 벡터를 고차원의 이미지로 변환하며, 저차원에서 고차원으로 데이터를 변환할 때 업샘플링 연산을 수행한다.
`세그멘테이션(segmentation)`은 이미지 영역을 분할하는 방법으로 각 영역에 속하는 픽셀들을 영역을 나타내는 클래스로 분류한다. 보통 세그멘테이션 모델은 다운샘플링과 업샘플링 단계로 구성되는데 다운샘플링 단계에서는 이미지의 특징을 학습하고 업샘플링 단계에선 학습된 특징을 이용하여 픽셀 단위로 클래스를 분류해 나간다. 업샘플링 단계에서 원래 이미지 크기로 복구할 때 업샘플링 연산을 수행한다. 컨벌루션 신경망에서는 주로 `언풀링(unpooling)`과 `트랜스포즈 컨벌루션(transposed convolution)`과 같은 방법으로 업샘플링 연산을 수행한다.
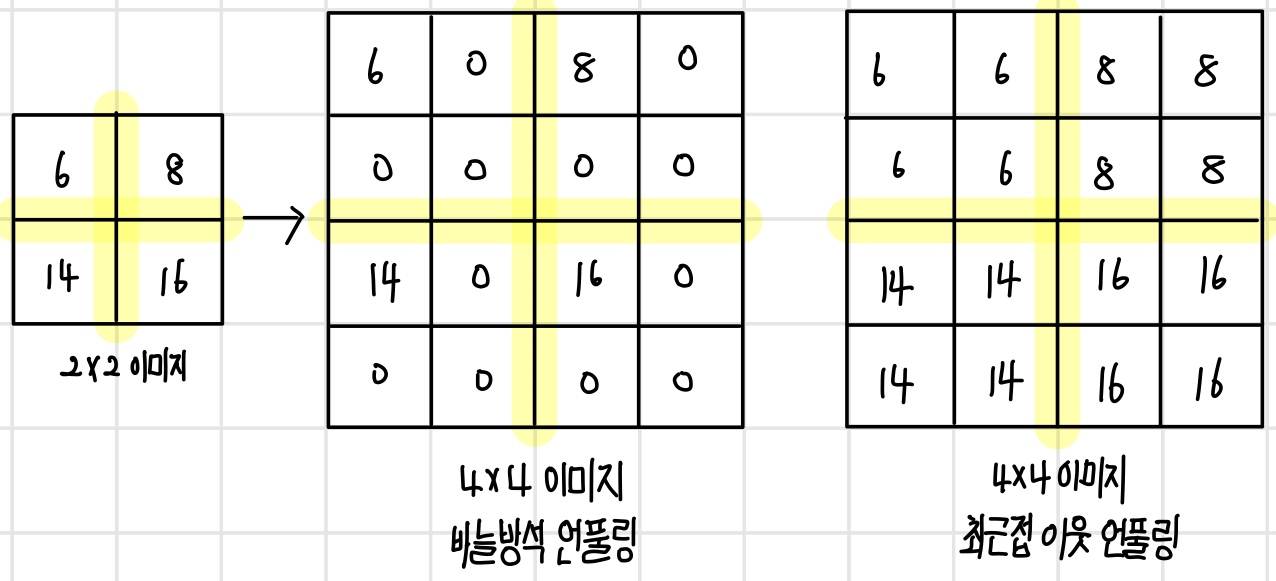
언풀링(unpooling)
언풀링은 풀링의 반대 연산으로, 요약된 통계 데이터를 요약하기 전 크기의 데이터로 복구하는 연산이다. 만약 (2 x 2) 크기의 이미지를 (2 x 2) 필터를 사용해서 (4 x 4) 이미지로 언풀링한다고 가정하면 각 픽셀을 어떤 값으로 채울지에 따라 다른 종류의 언풀링이 된다. 먼저 `바늘방석(bed of nails) 언풀링`은 (2 x 2) 영역의 첫 번째 픽셀은 원래의 값으로 채우고 나머지 픽셀은 0으로 채우는 방법이다. `최근접 이웃(nearest neighbor) 언풀링`은 (2 x 2) 영역을 모두 원래의 픽셀값으로 채우는 방법이다. 첫 번째 픽셀은 원래의 값으로 채우고 나머지 픽셀에는 가장 가까운 이웃인 첫 번째 픽셀과 같은 값으로 채운다.
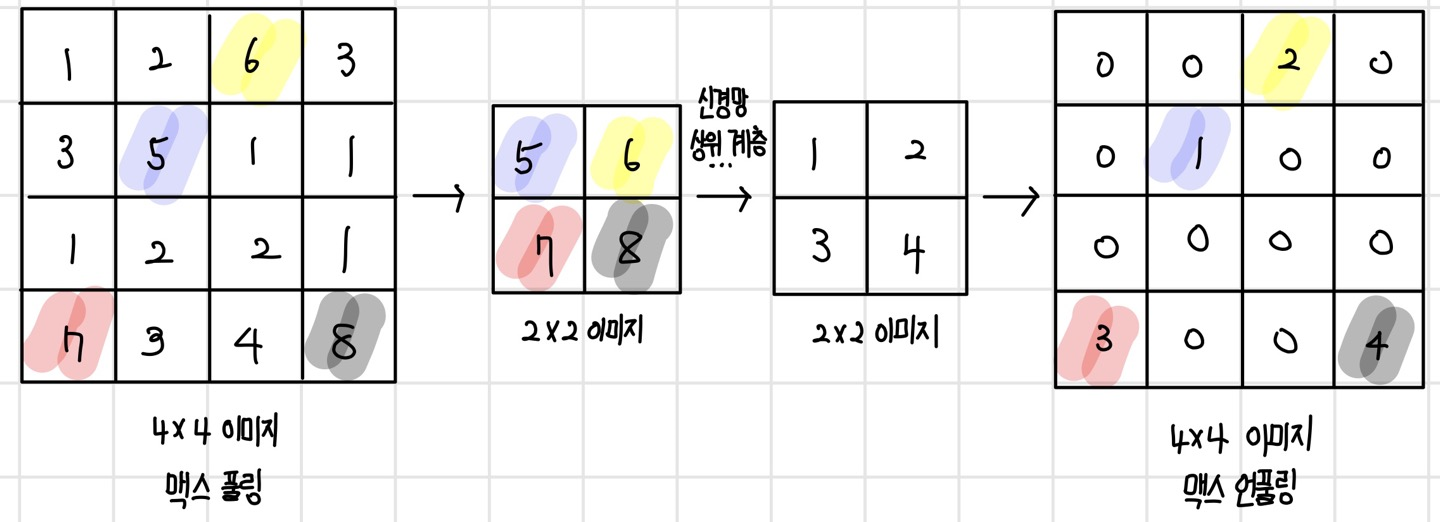
`맥스 언풀링(max unpooling)`은 다운샘플링과 업샘플링이 대칭을 이루는 모델 구조에서만 사용할 수 있는 방식이다. 맥스 풀링을 할 때 최댓값의 위치를 기억해 두었다가 언풀링을 할 때 기억해 둔 위치로 값을 복원하고 나머지는 0으로 채운다.
트랜스포즈 컨벌루션(transposed convolution)
언풀링 방식은 사전에 정의된 규칙에 의해 업샘플링을 수행하는데, 이 규칙은 모든 경우에 가장 적합한 방식일 보장이 없다. 따라서 때에 따라 가장 좋은 업샘플링 결과를 만들도록 규칙을 학습할 수도 있다. `트랜스포즈 컨벌루션(transposed convolution)`은 컨벌루션 필터를 학습하듯이 업샘플링 필터도 학습하도록 만든 방식이다.
만약 (2 x 2) 크기의 이미지를 (3 x 3) 크기의 트랜스포즈 컨벌루션 필터를 통해 (4 x 4) 크기의 이미지로 업샘플링 한다고 가정하자. 이 경우 입력 데이터의 첫 번째 픽셀과 트랜스포즈 컨벌루션 필터를 곱해서 (3 x 3) 크기의 출력 이미지 영역을 생성하고, 이후 입력 이미지의 두 번째 픽셀과 다시 필터를 곱해 오른쪽으로 두 칸 이동한 위치에 (3 x 3) 크기의 출력 이미지 영역을 생성한 뒤, 두 영역을 더해서 (5 x 5) 크기의 이미지를 생성한다. 이후 출력을 (4 x 4) 크기의 이미지로 만들기 위해 1픽셀을 삭제한다. 또한 스트라이드는 2인 경우 영역 간에 상하좌우로 1픽셀씩 겹치게 되는데, 겹치는 영역은 픽셀값을 더해준다.
트랜스포즈 컨벌루션 연산에서 주의할 점은 겹쳐진 부분의 픽셀값이 더해지면서 `바둑판무늬(checkerboard artifact)`가 생길 수 있다는 것이다. 바둑판무늬를 없애기 위해선 모든 픽셀이 같은 횟수로 겹쳐지도록 필터와 스트라이드의 크기를 조절해야 한다. 여기서 트랜스포즈 컨벌루션이란 이름이 붙여진 이유는 컨벌루션 행렬의 전치 행렬로 연산을 표현할 수 있기 때문이다.
이 포스팅은 'Do it! 딥러닝 교과서'를 공부하고 작성한 글입니다.